Business Midterm Exam Review Solutions Part 2
TLDRThe video script is a comprehensive guide for students preparing for a midterm exam in calculus, specifically tailored for a business course. The instructor emphasizes the importance of attempting problems independently before reviewing the solutions provided in the video. The document used for review is highlighted to distinguish between midterm and final exam materials. The solutions cover a range of calculus topics including limits, derivatives, and instantaneous rates of change, with an emphasis on understanding the process rather than just copying answers. The video also touches on the application of various derivative rules such as the power rule, product rule, quotient rule, and chain rule. The instructor provides a step-by-step approach to solving complex problems and encourages students to reach out for further clarification if needed. Additionally, the script includes an analysis of a graph to determine continuity, differentiability, and to calculate marginal profit in a business context. The summary serves as a reminder that true learning comes from engaging with the material and understanding the underlying concepts.
Takeaways
- 📚 **Active Engagement**: It's crucial to attempt solving problems before looking at the solutions to effectively review for an exam.
- 🖊️ **Note-Taking**: Keep track of the problems that are challenging and revisit those topics to improve understanding.
- 🚫 **Avoid Passive Learning**: Merely copying down solutions without understanding does not improve exam performance.
- 🔵 **Review Document**: The provided review document is color-coded to distinguish between midterm and final exam materials.
- 📈 **Limit Calculations**: For limits, it's important to substitute the variable with the given value and simplify, unless it results in division by zero, which requires algebraic manipulation.
- 🔄 **Continuity Check**: When evaluating limits, ensure that the function is continuous at the point of interest.
- 📉 **Piecewise Functions**: For piecewise functions, evaluate each piece to determine if the limit exists at specific points.
- 🔧 **Algebraic Skills**: Use algebra to simplify expressions and solve limits, such as factoring and canceling out terms.
- 📌 **Instantaneous Rate of Change**: The formal definition of the derivative can be used to find the instantaneous rate of change, involving a limit as h approaches zero.
- ⛓ **Chain Rule**: The chain rule is a fundamental method for finding derivatives of composite functions, where you differentiate the outer function and multiply by the derivative of the inner function.
- 🔢 **Product and Quotient Rules**: These rules are essential for finding derivatives of products and quotients of functions, involving manipulation of the functions and their derivatives.
Q & A
What is the main advice given by the lecturer at the beginning of the video?
-The lecturer emphasizes the importance of attempting each problem on the midterm exam review before watching the solutions. They stress that merely watching the solutions without personal effort won't improve one's understanding or exam score.
How does the lecturer categorize the review material for the midterm and final exams?
-The lecturer has underlined and circled in blue pen all the midterm material and underlined and circled in red pen all the final exam material to differentiate between the two.
What is the first limit problem discussed in the video?
-The first limit problem involves finding the limit as X approaches 2 of 3 times x cubed. The lecturer solves this by substituting x with 2 and finds the limit to be 24.
How does the lecturer approach the piecewise function limit problem in 1B?
-The lecturer evaluates each piece of the piecewise function at x equals 1 to determine if the limit exists. They find that the function is not continuous at x equals 1, as the values from the left and right approaches are not equal.
What algebraic technique does the lecturer use to solve the limit problem in 1C?
-The lecturer uses factoring, specifically recognizing a difference of squares, to eliminate the discontinuity and find the limit as X approaches 4, which results in a limit of 8.
How does the lecturer simplify the expression for the instantaneous rate of change in part two?
-The lecturer simplifies the expression by multiplying the numerator and denominator by the conjugate of the numerator, which allows for the cancellation of terms, eventually leading to the simplified expression of 3 over the square root of (3x + 3H + 4) + square root of (3x + 4).
What alternative method does the lecturer suggest to find the derivative in part two?
-The lecturer suggests using the derivative chain rule as an alternative method, which would be much easier and less time-consuming than using the formal definition of the derivative.
What is the derivative of the function in part 3A?
-The derivative of the function in part 3A is found to be 4X - 9, using the power rule for differentiation.
How does the lecturer approach the derivative problem in part 3E?
-The lecturer uses the quotient rule for derivatives, which involves finding the derivative of the numerator and the denominator separately and then applying the formula for the derivative of a quotient.
What is the main takeaway from the discussion on the instantaneous rate of change using the formal definition?
-The main takeaway is that while using the formal definition of the derivative can provide a deeper understanding, it is a more complex and time-consuming process. It's important to understand this method, but for practical purposes, shortcuts like the chain rule can be used.
How does the lecturer handle the derivative of an exponential function in part 3K?
-The lecturer uses the product rule for derivatives, treating the exponential function as the product of two functions, and then applies the chain rule to find the derivative of the inner function.
What is the derivative of the natural log function as discussed in part L?
-The derivative of the natural log function is 1 over X, as discussed in part L, which is a straightforward application of the derivative rules for logarithmic functions.
Outlines
📚 Midterm Exam Review Introduction
The speaker emphasizes the importance of attempting exam problems before watching the solutions video. They stress that simply watching the solutions won't improve understanding or exam scores. The video is a review for both a midterm and final exam in an online calculus course for business, with material clearly marked for each exam. The speaker plans to go through solutions quickly, having already covered the concepts in previous videos.
🔍 Limits and Derivatives: Formal Definition
The paragraph focuses on calculating limits and finding the instantaneous rate of change using the formal definition of the derivative. Examples given include finding the limit of a polynomial function, a piecewise function, and a function involving a difference of squares. The speaker simplifies expressions and uses algebraic techniques to solve for the limits. They also compare the formal definition method with the chain rule for derivatives as a more straightforward approach.
📝 Derivative Calculations and Rules
This section covers various problems involving the calculation of derivatives using different rules such as the power rule, product rule, quotient rule, and chain rule. The speaker provides step-by-step solutions for derivatives of functions like polynomials, roots, exponentials, and logarithms. They also rewrite expressions to simplify the application of these rules and remind viewers to apply the limit definition throughout the process.
🧮 Advanced Derivative Problems
The speaker tackles more complex derivative problems, using the product rule, chain rule, and quotient rule to find derivatives of composite functions, exponential functions, and logarithmic functions. They provide detailed steps for each derivative, emphasizing the importance of understanding the underlying mathematical concepts and rules. The speaker also makes a mistake and corrects it, showing the process of erasing and rewriting for clarity.
📉 Derivatives in Economics: Profit and Product Rules
The paragraph discusses the application of derivatives in economics, specifically in finding the marginal profit function from a total profit function. The speaker calculates the derivative and interprets the result at a specific point (200 cameras). They also address the concept of continuity and differentiability of a function represented on a graph, identifying points where the function is not differentiable due to discontinuities or vertical asymptotes.
🔁 Derivative Rules: Chain Rule and Quotient Rule
The speaker explains the use of the chain rule for finding derivatives of composite functions. They provide a formula for the chain rule and apply it to an example involving an expression with 'U' as an intermediate variable. The paragraph also covers the quotient rule for derivatives, showing how to simplify expressions before applying the rule. The speaker gives a detailed example of using the quotient rule to find the derivative of a quotient of two functions.
📈 Limit Evaluations and Function Behavior
This part of the script deals with evaluating limits as x approaches different values and assessing the continuity and differentiability of a function based on its graph. The speaker discusses how to interpret the graph to find limit values and to identify points of discontinuity and non-differentiability. They highlight the importance of understanding the behavior of the function at specific points and the implications for the existence of the derivative.
🔗 Conclusion and Upcoming Review Continuation
The speaker concludes the current video by noting that due to the length of the content, they will continue the review in another video. They indicate that the remaining part of the review will be addressed in the subsequent video, ensuring that the audience is aware that the material is divided into multiple parts for comprehensive coverage.
Mindmap
Keywords
💡Midterm Exam Review
💡Derivatives
💡Piecewise Function
💡Limit
💡Instantaneous Rate of Change
💡Formal Definition
💡Chain Rule
💡Product Rule
💡Quotient Rule
💡Continuous Function
💡Marginal Profit
Highlights
The importance of attempting exam review problems before watching the solutions video to ensure effective learning.
The necessity to identify and remediate knowledge gaps on problems that caused trouble.
The use of a review document that serves as a study guide for both midterm and final exams, with materials clearly marked for each exam.
The clear differentiation between midterm and final exam materials using blue and red pen for better organization.
The strategy to only cover the first half of the review document for the midterm exam.
The approach of quickly working through solutions without the teaching aspect, as teaching videos were provided separately.
The solution to a limit problem by direct substitution, showcasing a polynomial's continuity.
The method of evaluating piecewise function limits by checking the function's value at the point of interest.
The algebraic technique used to remove discontinuity in a limit problem by factoring and canceling out terms.
The formal definition of the derivative and its application in finding the instantaneous rate of change.
The use of the conjugate and the limit process to simplify the expression for a derivative, showcasing a step-by-step approach.
The verification of a derivative's result using the chain rule as a simpler alternative method.
The process of finding derivatives using the power rule, product rule, quotient rule, and chain rule for various functions.
The application of derivative rules to complex functions involving exponents, roots, and logarithms.
The reminder to reach out for help if confused about certain concepts or problems, emphasizing the availability of additional resources.
The interpretation of marginal profit in the context of total profit from the sale of cameras, with a practical example at a specific quantity.
The use of a graph to determine limits, continuity, and differentiability, with specific points analyzed for their mathematical properties.
Transcripts
Browse More Related Video

Business Midterm Exam Review Solutions Part 2

Polar, Parametric, Vector Multiple Choice Practice for Calc BC (Part 3)

AP Calculus Multiple Choice Practice Test (2020 AP CED Problems)
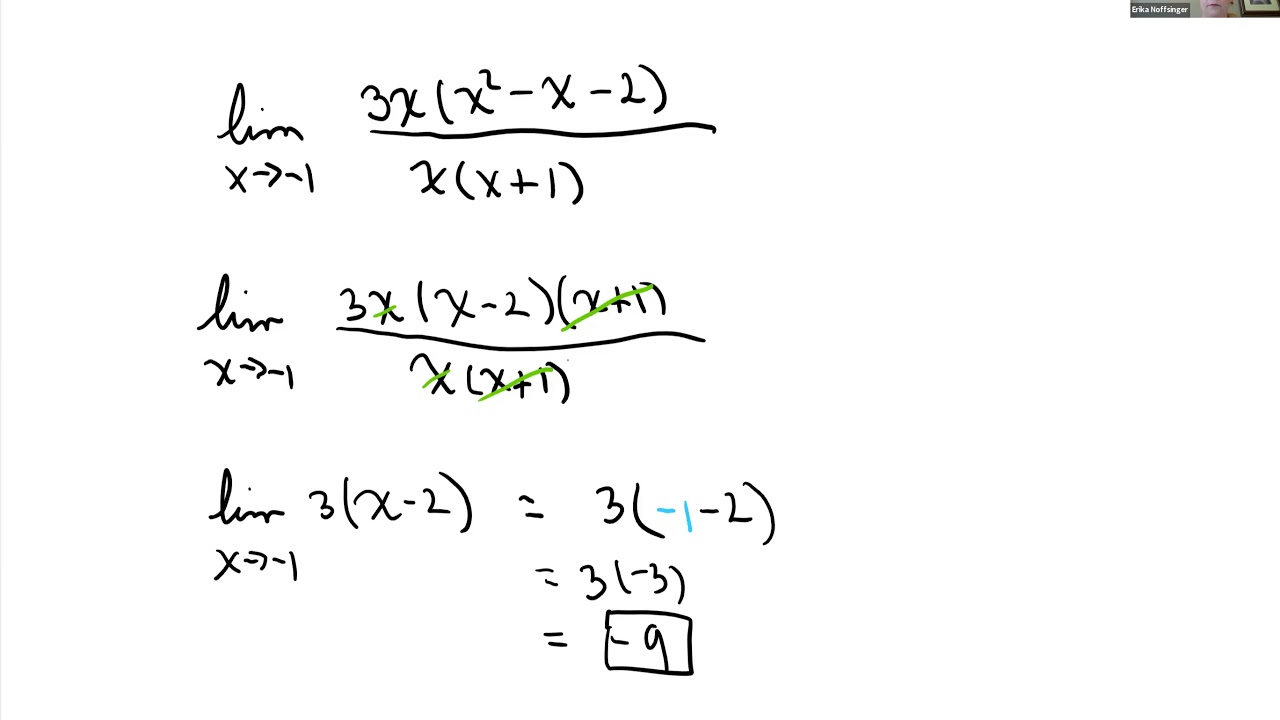
Business and Social Science Calculus Final Exam Review
AP Calculus AB 2003 Multiple Choice (no calculator) - Questions 1-28
AP Calculus AB 2012 Multiple Choice (no calculator) - Questions 1-28
5.0 / 5 (0 votes)
Thanks for rating: