Maximum / minimum [IB Maths AI SL/HL]
TLDRThe video script offers an insightful exploration into the application of derivatives in determining the maximum or minimum values of a function. It distinguishes between local and global maxima and minima, illustrating how a local maximum or minimum is a point where the function's value is higher or lower than its immediate surroundings, while a global maximum or minimum is the highest or lowest point across the entire function's domain. The presenter uses the concept of the derivative to explain how to identify stationary points—where the derivative equals zero—and further refines this by demonstrating that a change in the derivative's sign from positive to negative (or vice versa) indicates a local maximum or minimum, respectively. The script also covers the practical application of these concepts, including a step-by-step example of finding the maximum or minimum of a quadratic function using derivatives. Additionally, it touches on the sine diagram technique for confirming the nature of stationary points. The video concludes with a problem-solving scenario involving a function with an unknown constant, emphasizing the importance of understanding the underlying mathematical principles rather than relying solely on computational tools.
Takeaways
- 📌 Derivatives are used to find the maximum or minimum values of a function, known as local or global extrema.
- 🔍 A local maximum is the highest point in a certain area, whereas a global maximum is the highest point on the entire graph.
- 📈 A local minimum is the lowest point in a certain area, and it's identified by the same criteria as a local maximum but in reverse.
- 🧮 The derivative of a function at a point gives the gradient (slope) of the tangent line to the curve at that point.
- 🎓 Stationary points occur where the derivative equals zero, but they are not always maxima or minima; they could be points of inflection.
- 🔑 To determine if a stationary point is a maximum or minimum, check if the derivative changes sign from left to right.
- 📉 For a point to be a local maximum or minimum, the derivative at that point must be zero, and the sign of the derivative must change as you move from left to right across that point.
- 🤔 Analyzing the sign of the derivative at points to the left and right of a stationary point can confirm whether it's a maximum or minimum without graphing.
- 📐 The concept of a sine diagram is introduced as a method to visualize and confirm the nature of stationary points, especially in more complex or abstract scenarios.
- 💡 Even though calculators and graphing tools can find maxima and minima, understanding the underlying mathematical principles is crucial for solving problems where graphing isn't an option.
- ✅ To find a specific value, such as 'k' in a given function, one can use the condition that the derivative is zero at the point of interest and solve for the unknown.
- 📘 The process of finding the derivative, setting it to zero at a specific point, and solving for unknowns is a systematic approach to finding maxima, minima, and other stationary points.
Q & A
What does the derivative of a function tell us about its maximum or minimum?
-The derivative of a function tells us about the slope of the tangent line at a particular point. At a local maximum or minimum, the derivative is zero, indicating a flat tangent line, which corresponds to a stationary point.
What is the difference between a local maximum and a global maximum?
-A local maximum is the highest point in a particular area or 'local' neighborhood of the function, whereas a global maximum is the highest point of the function over its entire domain.
How can we identify a local maximum or minimum using the derivative?
-A local maximum or minimum can be identified when the derivative is zero and the sign of the derivative changes from left to right (or vice versa) across that point.
What is a stationary point and how does it relate to maxima and minima?
-A stationary point is a point where the derivative of the function equals zero. However, not all stationary points are maxima or minima; they could also be points of inflection where the function changes direction but does not reach a peak or trough.
Why do we need to check the sign of the derivative to the left and right of a stationary point?
-Checking the sign of the derivative to the left and right of a stationary point helps us determine whether the point is a maximum, minimum, or neither. If the derivative changes from positive to negative (or from negative to positive), it indicates a local maximum or minimum, respectively.
What is a sine diagram and how is it used in analyzing the behavior of a function's derivative?
-A sine diagram is a graphical tool used in calculus to visualize the sign of the derivative across different intervals of the function. It helps to determine the intervals where the function is increasing or decreasing and to identify local maxima and minima without plotting the entire function.
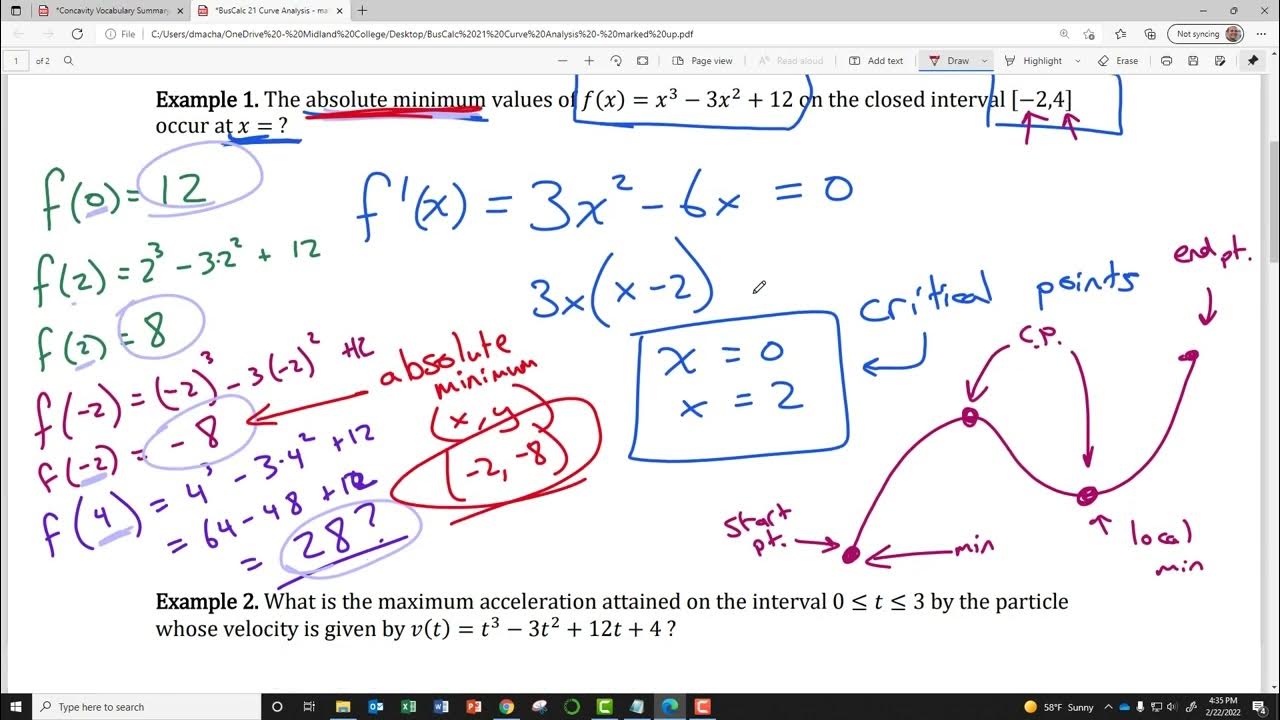
How can we find the maximum or minimum point of a quadratic function without using a calculator?
-We can find the maximum or minimum point of a quadratic function by first finding the derivative of the function, setting it equal to zero, and solving for x. Then, we substitute the x-value back into the original function to find the corresponding y-value, giving us the coordinates of the maximum or minimum point.
What is the significance of the second derivative test in determining the nature of a stationary point?
-The second derivative test involves finding the second derivative of the function and evaluating it at the stationary point. If the second derivative is positive, the point is a local minimum; if it's negative, the point is a local maximum; if it's zero, the test is inconclusive.
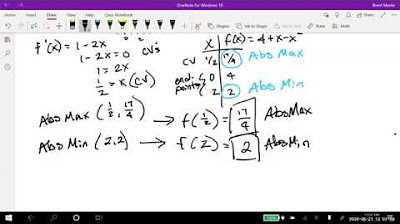
How does the concept of a local minimum apply when we are given a function with a parameter, like 'k'?
-When given a function with a parameter, such as 'k', we can still find local minima by setting the first derivative equal to zero and solving for x. If we need to find the value of 'k', we substitute the x-value of the local minimum into the derivative and solve for 'k'.
What is the role of the first derivative in determining the intervals of increase and decrease for a function?
-The first derivative indicates the slope of the tangent to the curve at any given point. If the first derivative is positive over an interval, the function is increasing on that interval. Conversely, if the first derivative is negative, the function is decreasing on that interval.
Why is it important to consider the behavior of the derivative at endpoints when analyzing a function over a closed interval?
-When analyzing a function over a closed interval, it is important to consider the behavior of the derivative at endpoints because the endpoints can also be points of local or global extrema. The derivative can help identify whether the endpoint is a maximum, minimum, or neither.
Outlines
📌 Understanding Maxima and Minima with Derivatives
The paragraph introduces the concept of using derivatives to identify the maximum or minimum values of a function. It distinguishes between local and global maxima and minima, explaining that a local maximum is a point where the function is at its highest within a confined area, whereas a global maximum is the highest point across the entire function. The importance of stationary points, where the derivative equals zero, is highlighted. However, it's noted that not all stationary points are maxima or minima, leading to the need for further criteria to identify them. The paragraph also explains that a local maximum or minimum occurs when the derivative is zero and changes sign from left to right.
🧮 Deriving the Derivative and Finding Extreme Points
This paragraph delves into the process of setting the derivative equal to zero to find potential maximum or minimum points of a function. It provides a step-by-step example using a quadratic function, showing how to calculate the derivative and solve for x when the derivative equals zero. The paragraph then demonstrates how to find the corresponding y-value to determine the coordinates of the extreme point. It also introduces the sine diagram technique to confirm whether a point is a maximum or minimum by examining the sign of the derivative to the left and right of the point in question.
🔍 Advanced Application: Finding a Local Minimum with a Variable
The final paragraph addresses a more complex scenario where a function includes a variable 'k', and the task is to find the value of 'k' for which the function has a local minimum at a specific point. The paragraph outlines the process of finding the derivative of the function and using the condition that the derivative at the point of local minimum is zero. By substituting the x-value of the local minimum into the derivative equation and setting it equal to zero, the paragraph shows how to solve for 'k', demonstrating that such problems can be solved systematically without relying on graphing calculators.
Mindmap
Keywords
💡Derivative
💡Local Maximum/Minimum
💡Global Maximum/Minimum
💡Stationary Point
💡Sign Change
💡Quadratic Function
💡Sine Diagram
💡Graphing Calculator
💡Contextual Problem Solving
💡Algebraic Manipulation
💡Inflection Point
Highlights
Derivatives are used to find the maximum or minimum of a function, which can be either local or global.
A local maximum is an area where the function is at its highest within a confined area, but not necessarily the highest overall (global maximum).
A global maximum is the highest point a function can reach over its entire domain.
A local minimum is a point where the function is at its lowest within a local area.
A stationary point is where the derivative of a function equals zero, but it is not always a maximum or minimum.
A local maximum or minimum is identified when the derivative is zero and changes sign from left to right.
The concept of a sine diagram is introduced as a method to analyze the change in the derivative's sign.
An example is given on how to find the maximum or minimum of a quadratic function by hand, using the derivative.
The process of setting the derivative equal to zero to find stationary points is demonstrated.
The importance of checking the sign of the derivative to the left and right of a stationary point to determine if it's a maximum or minimum is explained.
A method to determine whether a stationary point is a maximum or minimum using a sine diagram is shown.
The concept of a global maximum is introduced and demonstrated to be the highest point of a function over its entire domain.
A practical example involving a joke about minimum wage is used to illustrate the process of finding a maximum or minimum.
The process of solving for a variable (k) in a function when given a local minimum condition is demonstrated.
The importance of understanding the behavior of the derivative at a point to solve for unknowns in a function is emphasized.
The transcript concludes with a reminder that while calculators can be used, understanding the underlying principles is crucial for more complex problems.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: