Calculus: Maximum and minimum values on an interval
TLDRThe video script discusses solving mathematical problems related to critical points, maxima, minima, and concavity. The presenter tackles two problems: one involving a quadratic function defined on a closed interval and another involving a reciprocal function defined on an interval that includes zero. The first problem leads to the identification of a critical point and the determination of maximum and minimum values within the interval. The second problem explores the behavior of the function near points where the derivative is undefined and concludes that there are no maximum or minimum points due to the function's asymptotic behavior towards positive and negative infinity at zero.
Takeaways
- 📚 The problem involves identifying critical points and finding maxima and minima of a function within a given interval.
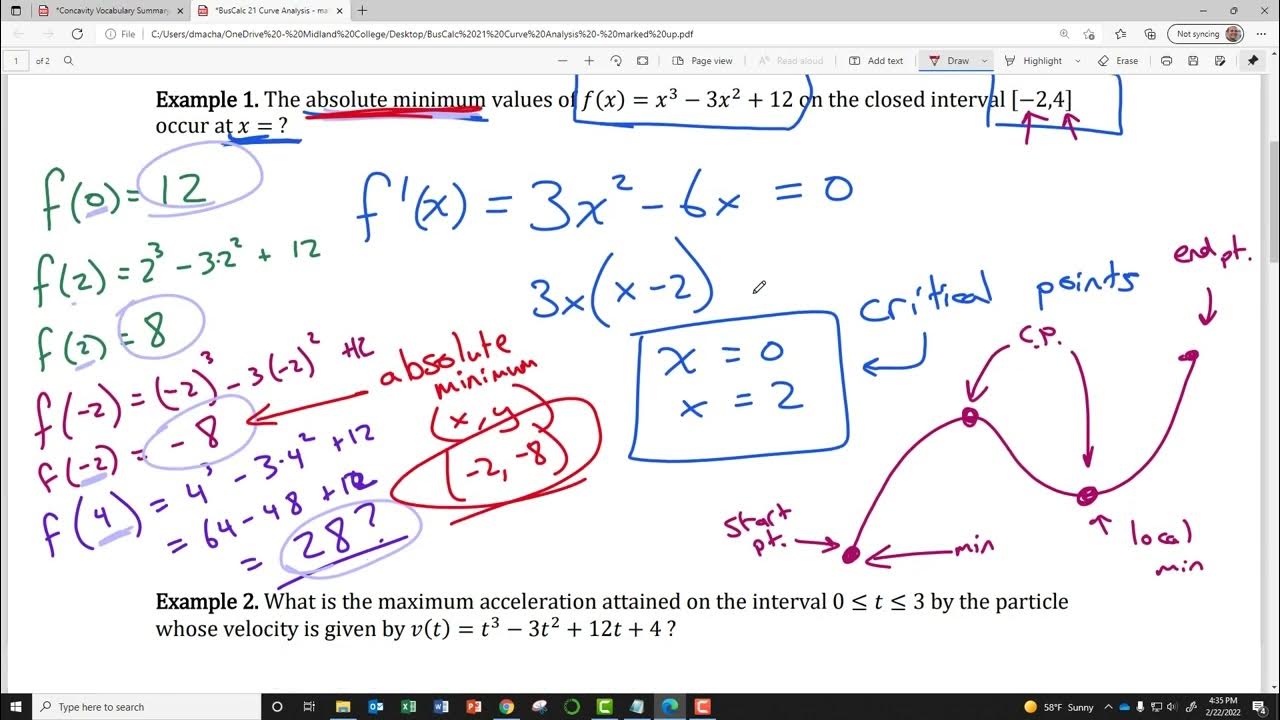
- 🔍 The function f(x) is given as f(x) = x^2 + 4x + 4, and the interval of interest is [-4, 0], including both endpoints.
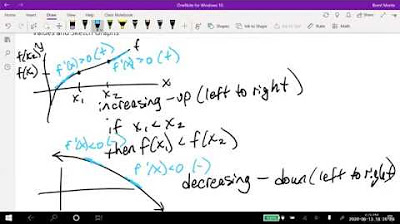
- 🤔 Critical points are defined as points where the derivative is zero or does not exist. For this problem, the derivative is f'(x) = 2x + 4.
- 👉 By setting the derivative equal to zero, x = -2 is found to be the critical point within the interval.
- 📈 The value of the function at the critical point is f(-2) = 0, which is the coordinate of the critical point.
- 📊 Evaluating the function at the endpoints of the interval gives f(-4) = 4 and f(0) = 4, which are potential maximum points.
- 📈 The graph of the function is a parabola, and the critical point is symmetrically located between the endpoints.
- 🔄 The second derivative test is mentioned, indicating that the second derivative f''(x) = 2 is positive, suggesting the function is concave up and thus the critical point is a minimum.
- 📚 The second problem involves the function h(r) = 1/r over the interval [-1, 3], including both endpoints.
- 🤔 The derivative h'(r) = -1/r^2 does not equal zero within the interval, and it is undefined at r = 0, which is within the interval.
- 📊 The graph of h(r) has asymptotic behavior, approaching positive infinity as r approaches 0 from the right and negative infinity as r approaches 0 from the left.
- 🚫 There are no maximum or minimum points in the traditional sense for h(r) over the interval, as the function approaches infinity in both directions.
Q & A
What are the main topics discussed in the video?
-The main topics discussed in the video are critical points, maxima, minima, and concavity. The speaker also explains the concept of open and closed intervals and demonstrates how to identify critical points and find maximum and minimum values on a given interval using two specific functions.
How are critical points defined in the context of this video?
-In the context of this video, critical points are defined as points where the derivative of a function is either zero or does not exist.
What is the first function given in the video, and what is the interval of interest?
-The first function given in the video is f(x) = x^2 + 4x + 4, and the interval of interest is from -4 to 0, inclusive of both endpoints.
How does the speaker find the critical point for the first function?
-The speaker finds the critical point for the first function by setting the derivative, f'(x) = 2x + 4, equal to zero and solving for x, which results in x = -2.
What are the maximum and minimum values of the first function on the given interval?
-The maximum values of the first function on the given interval are at the endpoints, x = -4 and x = 0, with both having the value of 4. The minimum value is at the critical point, x = -2, with a value of 0.
What is the second function discussed in the video, and what is its interval?
-The second function discussed in the video is h(r) = 1/r, and the interval of interest is from -1 to 3, inclusive of both endpoints.
Why is r = 0 not considered a critical point for the second function?
-r = 0 is not considered a critical point for the second function because although the derivative is undefined at that point, the function itself is also undefined at r = 0. The speaker defines a critical point as a point where the derivative is either zero or undefined but the function is defined.
What happens to the values of the second function as r approaches 0?
-As r approaches 0, the values of the second function approach positive infinity from the right and negative infinity from the left, meaning the function has no defined maximum or minimum points within the interval.
How does the speaker describe the graph of the second function?
-The speaker describes the graph of the second function as asymptoting to negative infinity on the left side and positive infinity on the right side, with the graph being undefined at r = 0.
What is the significance of the concavity theorem mentioned in the video?
-The concavity theorem is mentioned to provide additional insight into the behavior of the function at the critical point. The speaker suggests that the second derivative being positive indicates that the slope is increasing, which helps to confirm that the critical point is a minimum for the function.
How does the speaker plan to continue the discussion of these mathematical concepts?
-The speaker plans to continue the discussion of these mathematical concepts in a future video, as indicated by the end of the transcript.
Outlines
📚 Critical Points and Extrema in Calculus
The speaker begins by discussing a calculus problem involving critical points, maxima, minima, and concavity. They explain that critical points are where the derivative is zero or undefined. The given function is f(x) = x^2 + 4x + 4, and the interval of interest is from -4 to 0, inclusive. The speaker calculates the derivative, f'(x) = 2x + 4, and finds the critical point at x = -2 where the derivative equals zero. They then evaluate the function at the endpoints of the interval, finding f(-4) = 4 and f(0) = 4. The speaker also discusses the concept of concavity and the second derivative, which is positive for the given function, indicating an increasing rate of change of the slope. They conclude that the minimum value on the interval is at the critical point (-2, 0), and the maximum values are at the endpoints (-4, 4) and (0, 4).
🔍 Understanding Critical Points in Functions
In this paragraph, the speaker moves on to a second calculus problem involving the function h(r) = 1/r. The interval of interest is from -1 to 3, inclusive. The speaker explains that critical points occur where the derivative is zero or undefined. They note that while the derivative h'(r) = -1/r^2 is undefined at r = 0, this is not considered a critical point because the function itself is also undefined at this point. The speaker then describes the graph of h(r), noting that it approaches negative infinity as r approaches 0 from the left and positive infinity as r approaches 0 from the right. They plot key points and discuss the asymptotic behavior of the function on the given interval. The speaker concludes that there are no maximum or minimum points on the interval because the function approaches infinity at r = 0 and goes to negative infinity at the lower end.
🤔 Reflecting on Maximum and Minimum Points
The speaker concludes the video by reflecting on the concept of maximum and minimum points in the context of the functions discussed. They reiterate that the graph of h(r) does not have a defined maximum or minimum value at r = 0, as the function approaches both positive and negative infinity from different directions. The speaker emphasizes the importance of understanding the behavior of functions and their derivatives, especially at points where the derivative is undefined. They wrap up the video by mentioning their intention to continue exploring these problems in a future video, acknowledging the value of concise educational content while also expressing appreciation for the flexibility provided by YouTube's platform.
Mindmap
Keywords
💡Critical Points
💡Derivative
💡Maximum and Minimum Values
💡Interval
💡Concavity
💡Asymptote
💡Second Derivative
💡Slope
💡Graphing
💡Function Values
💡Undefined
Highlights
The discussion begins with the presenter agreeing to solve a set of problems on critical points, maxima, minima, and concavity, which were sent by a user named Akosh.
The first problem involves identifying critical points and finding the maximum and minimum values of the function f(x) = x^2 + 4x + 4 on a closed interval from -4 to 0.
The concept of critical points is explained as points where the derivative is either zero or does not exist within the given interval.
The derivative of the function f(x) is found to be f'(x) = 2x + 4, and the critical point is determined by setting the derivative equal to zero, resulting in x = -2.
The function is evaluated at the critical point x = -2, yielding f(-2) = 0, which is the coordinate of the critical point.
The function is also evaluated at the endpoints of the interval, resulting in f(-4) = 4 and f(0) = 4.
A graph of the function over the interval is discussed, with the critical point being the对称轴 of the parabola and having a slope of zero.
The second problem involves the function h(r) = 1/r on an interval from -1 to 3, including the endpoints.
The derivative of h(r) is calculated as h'(r) = -1/r^2, and it is noted that the derivative never equals zero and is undefined at r = 0.
The function h(r) is undefined at r = 0, and the same is true for its derivative, so r = 0 is not considered a critical point.
A graph of h(r) is described, showing asymptotic behavior towards positive and negative infinity as r approaches 0.
The function h(r) has no maximum or minimum points within the interval because it approaches infinity as r gets closer to 0 from either direction.
The presenter emphasizes the importance of understanding the problem and terminology, as it can often be more confusing than the problem itself.
The presenter mentions that the next set of problems will be continued in a future video, indicating a series of educational content.
The discussion concludes with the presenter acknowledging that they have exceeded the typical 10-minute video length due to viewer preference for concise knowledge sharing.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: