Math 1325 Lecture 12 1
TLDRLecture 12.1 of Math 1325 delves into the concept of integrals, the second major operation in calculus, which complements derivatives by quantifying accumulated change over time. The lecture distinguishes between derivatives, which measure instantaneous change or slope, and integrals, which assess the total change. Integrals are presented as anti-derivatives, with the process of finding an integral termed 'integration.' The indefinite integral is introduced as a formula or function found without specific values, symbolized by the integral sign and the integrand, which is the function being integrated with respect to a variable, often x. The lecture covers fundamental rules of integration, such as the integral of a constant times a function being equal to the constant times the integral of the function, and the power rule for integration, which reverses the process of differentiation for power functions. Practical examples illustrate these concepts, including calculating the integral of 2x, which results in x^2 + C, and correcting a mistake in the integration of a cube root function. The lecture concludes with a word problem involving sales records, where the marginal revenue function is integrated to find the total revenue function for a product, emphasizing the importance of determining the constant of integration to accurately calculate total revenue for a given quantity sold.
Takeaways
- 📚 The second major operation in calculus after derivatives is integrals, which measure accumulated change over time, as opposed to instantaneous change.
- 🔍 Integrals are the inverse function (anti-derivative) of derivatives, effectively 'undoing' the process of differentiation.
- ✅ When integrating a function like x^2 + 4, the result is x^3 + C, where C is a constant that accounts for the potential original function's constant term.
- 📈 The integral sign (∫) is used to denote the process of integration, and dx indicates integration with respect to the variable x.
- 🔢 Basic integral rules include the integral of a constant times a function being equal to the constant times the integral of the function, and the ability to integrate sums and differences by integrating each part separately.
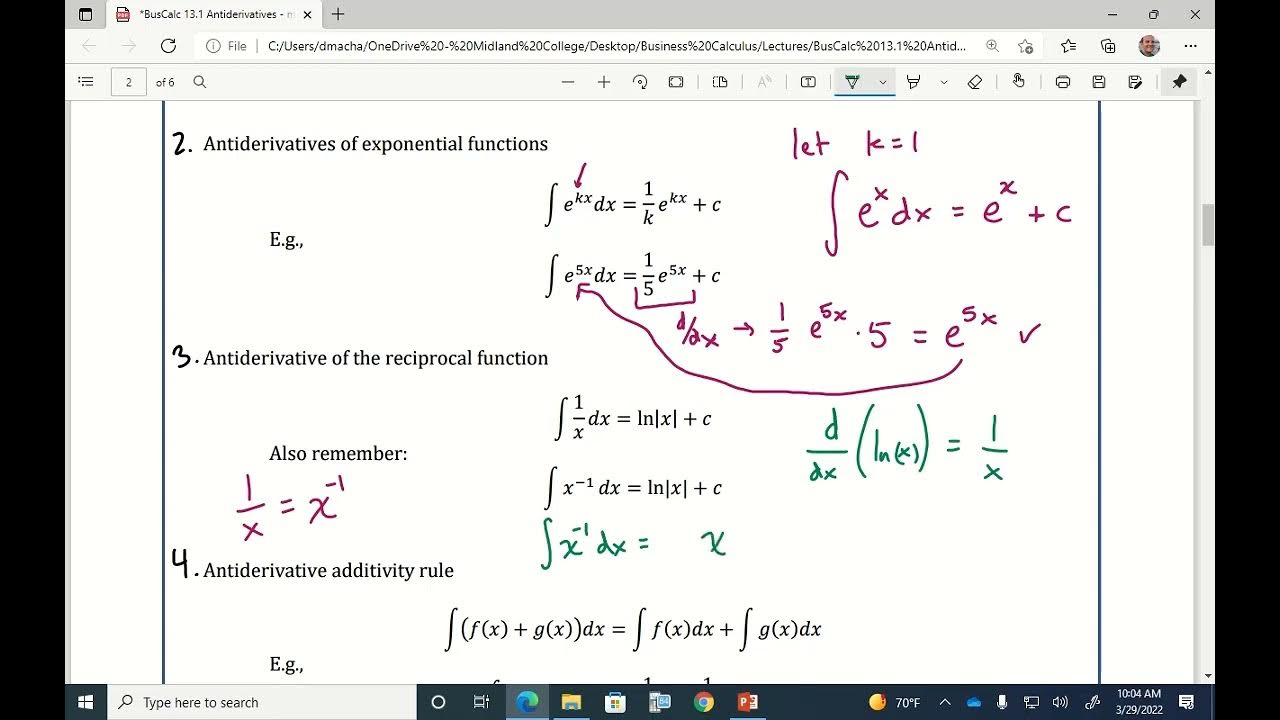
- 📝 The power rule for integration states that the integral of x^n is (1/(n+1))x^{n+1} + C, where n is a constant.
- 🧮 Integration of functions like sqrt(x) can be rewritten as a power function x^{1/3} and then integrated using the power rule.
- ❌ Errors can occur during integration, such as incorrect coefficients, which should be corrected to maintain mathematical accuracy.
- 🔧 Integration can be used to solve real-world problems, such as finding the total revenue function from a marginal revenue function, by integrating the rate of change of revenue.
- 💡 To find a specific value, like total revenue for a certain quantity sold, plug the quantity into the total revenue function and calculate the result.
- 📉 In word problems, especially with revenue or cost functions, it's important to determine the value of the constant of integration (if any) using given conditions, like revenue at zero sales.
Q & A
What is the main focus of Lecture 12.1 in the Math 1325 course?
-The main focus of Lecture 12.1 is to introduce and discuss the concept of integrals in calculus, which are the opposite or the inverse function of derivatives and represent accumulated change over time.
What is the relationship between derivatives and integrals?
-Derivatives represent the rate of instantaneous change, providing the slope of a curve at a specific point. Integrals, on the other hand, are the anti-derivatives and tell us the accumulated change over a period of time.
How does the process of integration relate to finding an integral?
-Integration is the process of finding an integral or an anti-derivative. An indefinite integral is a function or formula found without specific values, which represents the family of functions that could be the antiderivative of the integrand.
What is the integral sign in calculus and what does 'dx' signify?
-The integral sign, represented by a large 'S', is used to denote the process of integration. The 'dx' signifies that the integration is being performed with respect to the variable 'x'.
What is the power rule for integration and how does it relate to the power rule for differentiation?
-The power rule for integration states that when integrating a power function, you bring the power down in front, add one to the power, and then divide by the new power. It is the reverse of the power rule for differentiation, which involves bringing the power down and subtracting one from the exponent.
How does the integral of a constant differ from the integral of a variable?
-The integral of a constant is simply the constant multiplied by 'x' plus the constant of integration 'C'. In contrast, the integral of a variable involves applying the power rule (if it's a power function) or other appropriate integration techniques, and always includes the addition of the constant of integration 'C'.
What is the sum and difference rule for integration and how does it relate to differentiation?
-The sum and difference rule for integration allows you to integrate each part of a sum or difference separately and then add or subtract the results. This is similar to the rule for differentiation, where you can differentiate each part of a sum or difference and then add or subtract the results.
What is a composite function in the context of integration?
-A composite function in the context of integration is a function that is composed of another function, often with the outer function being a polynomial and the inner function being raised to a power or being a root. Integration of composite functions may require expanding the function before applying the power rule or other integration techniques.
How is the total revenue function derived from the marginal revenue function?
-The total revenue function is derived from the marginal revenue function by taking the integral of the marginal revenue function. Since the marginal revenue is the derivative of the revenue function, integrating it will give us the original revenue function, which represents the total revenue.
Why is it necessary to determine the value of the constant 'C' in the revenue function?
-The constant 'C' needs to be determined to find the exact revenue function that corresponds to the given marginal revenue function. In the context of revenue, setting 'C' to zero is logical because total revenue should be zero when no units are sold.
How is the total revenue calculated for the sale of 1,000 motherboards?
-To calculate the total revenue for the sale of 1,000 motherboards, you plug the quantity (1,000) into the determined revenue function, which is 300x - 0.1x^2 after setting the constant 'C' to zero. This yields the total revenue for the specified quantity.
Outlines
📚 Introduction to Integrals and Their Relationship with Derivatives
This paragraph introduces the concept of integrals as the second major operation in calculus, following derivatives. It explains that while derivatives measure instantaneous change or the slope at a particular point on a curve, integrals measure the accumulated change over a period. Integrals are the inverse function of derivatives, often referred to as anti-derivatives. The paragraph gives an example of finding the integral of 2x, which results in x^2 + C, highlighting the constant of integration. It also touches on the notation and terminology associated with integrals, such as the integral sign (∫), the integrand, and the dx, which indicates integration with respect to x. The concept of the power rule for integration is introduced, which is the reverse process of differentiation for power functions.
🔢 Integration Rules and the Power Rule
The second paragraph delves into the rules of integration, emphasizing the linearity of the integral operation, which allows the integration of a sum or difference of functions to be broken down into the integration of each part. It also discusses the integral of a constant times a function, which is equal to the constant times the integral of the function. The power rule for integration is detailed, showing how to integrate power functions by adjusting the exponent. Examples are provided to illustrate the application of the power rule, including correcting a mistake in the calculation of the integral of x^(1/3), which should be 4/3x^(4/3) instead of the initially stated 4/3x^(3/4). The paragraph concludes with a recommendation to practice integrating various functions using the power rule.
🧮 Applying Integration to Polynomials and Composite Functions
The third paragraph continues the discussion on integration by applying it to polynomials and composite functions. It demonstrates the process of integrating each term of a polynomial separately and then combining the results. A composite function, such as (x^2 - 4)^2, is also integrated by first expanding it and then integrating each term. The paragraph emphasizes the importance of including the constant of integration (C) in the final answer. It concludes with a word problem related to sales records, where the marginal revenue function is given, and the total revenue function is found by integrating the marginal revenue. The process of finding the total revenue for a specific quantity sold, in this case, 1,000 motherboards, is outlined.
💼 Calculating Total Revenue from Sales Using Integration
The final paragraph focuses on a word problem involving the calculation of total revenue from the sale of motherboards. Given the marginal revenue function, the total revenue function is derived by integrating the marginal revenue. The integral of each term of the marginal revenue function is calculated, resulting in the total revenue function. To find the value of the constant of integration, C, the fact that revenue is zero when no units are sold is used, which leads to determining that C equals zero. The total revenue for selling 1,000 motherboards is then calculated by substituting the quantity into the total revenue function, resulting in a revenue of $200,000. The paragraph ends with a note on the importance of not leaving the constant C in a word problem function and a wish for a productive and enjoyable weekend for the students.
Mindmap
Keywords
💡Integrals
💡Derivatives
💡Anti-derivative
💡Power Rule
💡Indefinite Integral
💡Constant of Integration
💡Integration
💡Marginal Revenue
💡Total Revenue Function
💡Composite Function
💡Word Problem
Highlights
The lecture introduces the concept of integrals as the second major function in calculus, contrasting them with derivatives which represent instantaneous change.
Integrals measure accumulated change over time, serving as the anti-derivative or inverse function of derivatives.
The integral of a function like x^2 + 4 results in x^2 + C, where C represents an unknown constant that could be any value due to the derivative of a constant being zero.
Integration is the process of finding an integral or anti-derivative, with the integral sign '∫' and dx indicating integration with respect to the variable x.
Basic rules of integration are discussed, including the integral of a constant times a function being equal to the constant times the integral of the function.
The power rule for integration is introduced, which states that the integral of x^n is (x^(n+1))/(n+1) + C.
The importance of adding a constant 'C' to the result of an indefinite integral is emphasized, as it accounts for the potential presence of a constant in the original function.
The process of integrating a sum or difference of functions is explained, which parallels the derivative rule that allows the integration of each part separately and then combining the results.
An example of integrating x^3 using the power rule is demonstrated, resulting in (1/4)x^4 + C.
A correction is made to a previous calculation error regarding the integral of the cube root of x, emphasizing the need for accuracy in mathematical processes.
The concept of a composite function is introduced, where a function is inside another function, and the outer function is squared, leading to a more complex integration process.
The integration of a polynomial function, such as x^4 - 8x^2 + 16, is demonstrated by breaking it down into simpler parts and integrating each part.
A real-world application of integration is presented through a word problem involving the total revenue function for a motherboard based on its marginal revenue.
The marginal revenue function is integrated to find the total revenue function, illustrating the practical use of anti-derivatives in economics.
The calculation of the total revenue for selling 1,000 motherboards is performed, showcasing how to apply the total revenue function to find specific values.
The importance of setting the constant 'C' to zero in practical applications, such as revenue functions, is discussed to reflect real-world scenarios where no revenue is generated without sales.
The lecture concludes with a summary of the key concepts and an encouragement for students to apply what they've learned to their homework.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: