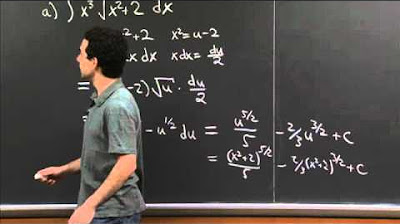Integration by Substitution (Introduction)
TLDRIn this educational video from Excellence Academy, the instructor explores the method of integration by substitution. The tutorial begins with a basic introduction to why substitution is necessary when standard integration methods fall short, using an illustrative example involving the integral of a polynomial raised to a power. The instructor methodically demonstrates how to choose a substitution variable, perform the necessary differentiation, and substitute back into the integral. Two detailed examples are worked through, showing the steps of substitution, simplifying the integral, and integrating using the general method. This comprehensive guide aims to equip viewers with the skills to tackle complex integrals using the substitution method.
Takeaways
- 📚 The method of substitution is used for integration when the integral cannot be done with the given variable.
- 🔑 A single variable (like 'u') is chosen to represent a more complex expression to simplify the integration process.
- 🧮 The substitution 'u' is set equal to a part of the integral, and then differentiated with respect to 'x' to find du/dx.
- 🔁 After finding du/dx, the integral is rewritten in terms of 'u' and du, allowing for easier integration.
- 🔄 The original variable 'x' and its differential dx are expressed in terms of 'u' and du for the substitution.
- 📈 The integral is then evaluated with respect to 'u', often simplifying the problem significantly.
- 🎛️ Constants are moved outside the integral sign when possible to simplify the integration.
- ✅ The final step is to substitute the original expression (that we set 'u' equal to) back into the simplified integral.
- 🔢 The method can be applied to a variety of integrals, including those with roots or powers that complicate direct integration.
- 📉 When integrating with respect to 'u', it may be necessary to express 'x' in terms of 'u' to proceed.
- ➗ The integral of 'x' with respect to 'u' is not always straightforward and requires algebraic manipulation to isolate 'u'.
Q & A
What is the method of integration discussed in the video script?
-The method of integration discussed in the video script is substitution.
Why is substitution used in integration?
-Substitution is used in integration when the integral variable needs to be changed to a suitable variable for the integration to be feasible.
Can all integrals be solved using the given integral variable?
-No, some integrals cannot be solved using the given integral variable, hence the need for substitution.
What variable is often used in substitution?
-A single alphabet, such as 'u', is often used to represent the new integral variable after substitution.
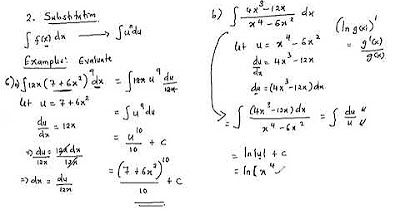
How is the substitution method applied to the integral of 8x(3x^2 - 7)^19?
-In the example provided, 'u' is defined as 3x^2 - 7. Then, the integral is expressed in terms of 'u', leading to the integration of 8x in terms of 'u'.
What is the integral of 8x with respect to 'u' after substitution?
-The integral of 8x with respect to 'u' after substitution becomes (4/3)u^20.
How is the value of 'u' substituted back into the equation after integration?
-After integration, the value of 'u' is substituted back into the equation to obtain the final answer.
What is the final answer after substituting the value of 'u' back into the equation?
-The final answer after substituting the value of 'u' back into the equation is (3x^2 - 7)^520 / 15, plus a constant.
How is substitution applied to the integral of 3x / √(4 - x)?
-In this case, 'u' is defined as √(4 - x), and after substitution, the integral is expressed in terms of 'u'.
What is the final answer after integrating 3x / √(4 - x) using substitution?
-The final answer after integrating 3x / √(4 - x) using substitution is -24u + 2u^3 + c, where 'u' is equal to √(4 - x).
Outlines
📚 Introduction to Integration by Substitution
The first paragraph introduces the concept of integration by substitution, a method used when direct integration with the given variable is not feasible. The speaker uses the example of integrating \(8x \cdot (3x^2 - 7)^{19}\) and demonstrates the substitution process by setting \(u = 3x^2 - 7\), differentiating \(u\) with respect to \(x\), and then substituting \(u\) back into the integral. The process involves changing the integral variable to simplify the expression and solve the integral, which in this case results in \(\frac{2}{3}u^{20} + C\), where \(C\) is the constant of integration.
🧮 Applying the Substitution Method to a New Example
The second paragraph continues the discussion on the substitution method by tackling another integral, \(\int \frac{3}{\sqrt{4 - x}} dx\). The speaker chooses \(u = \sqrt{4 - x}\) and proceeds to differentiate \(u\) implicitly to find the relationship between \(du\) and \(dx\). The integral is then transformed in terms of \(u\) and solved, resulting in \(-24u + \frac{2}{3}u^3 + C\). The speaker emphasizes the importance of expressing \(x\) in terms of \(u\) for proper integration and concludes by substituting the value of \(u\) back into the equation to obtain the final answer in terms of \(x\).
🔍 Detailed Walkthrough of Substitution in Integration
The third paragraph delves deeper into the substitution method by revisiting the integral from the second paragraph. The speaker explains the process of expressing \(x\) in terms of \(u\) using the relationship \(u^2 = 4 - x\), which simplifies the integral to \(-6 \int u du\). The integral is then solved, and constants are moved outside the integral sign. The final step involves substituting the original expression for \(u\) back into the solution to obtain the integral's value in terms of \(x\). The paragraph concludes with the final answer to the integral, showcasing the method's effectiveness in solving complex integrals.
Mindmap
Keywords
💡Integration
💡Substitution Method
💡Integral Variable
💡Differentiation
💡U-Substitution
💡Definite Integral
💡Indefinite Integral
💡Chain Rule
💡Constants
💡General Method
💡Integration by Parts
Highlights
Introduction to the method of substitution for integration, which is used when the given integral variable cannot be used directly for integration.
Demonstration of substitution using the algebraic representation of integral expressions, such as letting u = 3x^2 - 7 to simplify integration.
Differentiation of the substitution variable u with respect to x to find du/dx, which is a key step in the substitution method.
Use of the chain rule to express dx in terms of du, which allows for the transformation of the integral into a more manageable form.
Substitution of the original integral into the new form using u, which simplifies the integration process.
Integration of the new expression with respect to u, which often leads to a more straightforward solution.
Application of the power rule for integration, which is a fundamental technique in solving integrals involving powers of the substitution variable.
Substitution of the original variable back into the final expression to obtain the solution in terms of the original integral variable.
Explanation of the importance of including the constant of integration, denoted by 'c', in the final solution.
Second example using the substitution method to integrate 3/√(4-x), showcasing the versatility of the technique.
Use of implicit differentiation to find the relationship between dx and du when the substitution variable is a root or fractional expression.
Transformation of the integral to express it solely in terms of u, which simplifies the process of integration.
Strategy for moving constants outside the integral sign to simplify the integration process.
Integration of polynomial and power functions of u, which is a common step in the substitution method.
Final substitution of the original variable x back into the integrated expression to provide the solution in the original context.
Emphasis on the methodical approach of the substitution technique, which involves differentiating, substituting, integrating, and then back-substituting.
Illustration of how to handle the constant term when integrating and the importance of including it in the final answer.
The final answer of the integration problem is presented, demonstrating the successful application of the substitution method.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: