The Mandelbrot Set Explained
TLDRThe video script delves into the intricate beauty of the Mandelbrot set, a fractal shape with infinite detail calculated using complex numbers. It explains the concept of deterministic chaos, where small changes in initial conditions can lead to vastly different outcomes, famously known as the butterfly effect. The script simplifies the exploration of the Mandelbrot set using basic mathematics and visual explanations, focusing on the iterative process of calculating the equation Z squared plus C. It highlights the behavior of the set's orbits, identifying fixed points, and the importance of the value of C in determining whether orbits remain localized or escape to infinity. The video also introduces the concept of complex numbers and their role in expanding the Mandelbrot set into a two-dimensional space. It concludes by discussing the practical applications of the set in computer graphics and the fascination it holds for mathematicians due to its chaotic yet patterned behavior, hinting at a future exploration of Julia Sets and their relation to the Mandelbrot set.
Takeaways
- 🌀 The Mandelbrot set is a fractal with infinite shapes and patterns, calculated using complex numbers.
- 🔍 The set is explored through iteration of the equation Z squared plus C, which can lead to chaotic behavior.
- 🎨 The black part of the Mandelbrot set represents the actual set, while the colored area is outside it.
- 📏 Initially, the explanation is restricted to one dimension, focusing on the central line of real numbers.
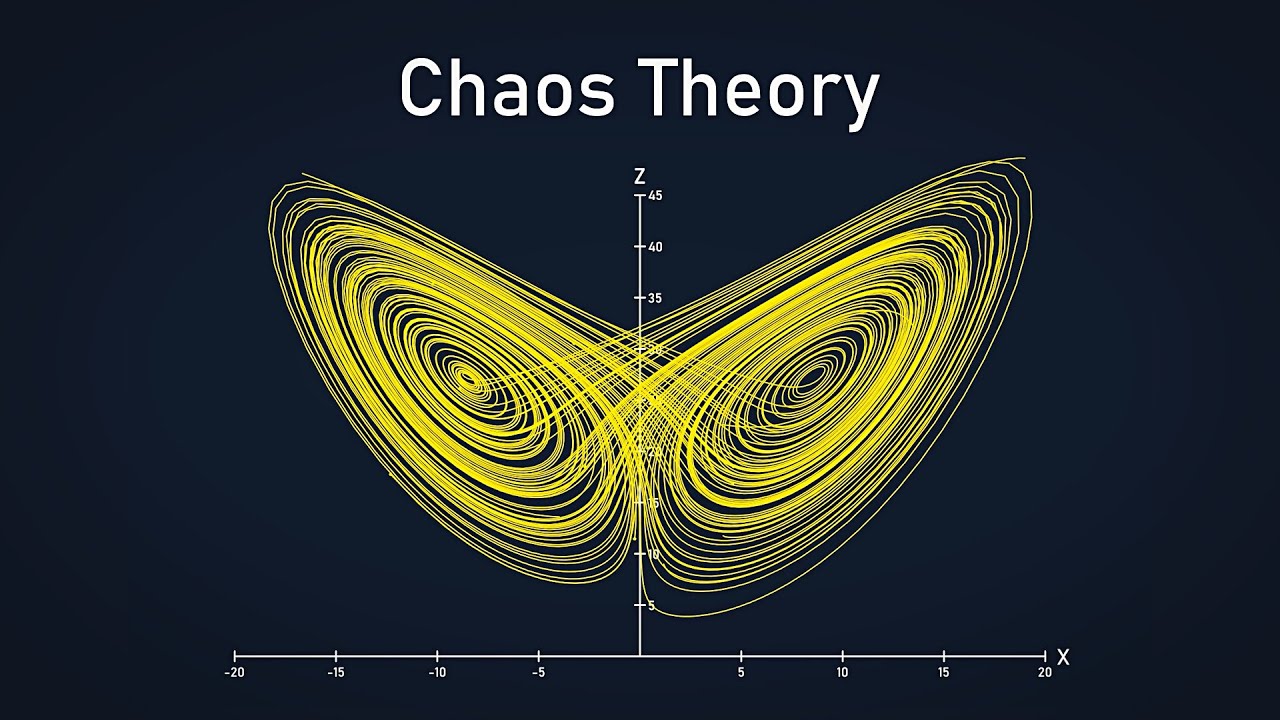
- 🌐 Chaos theory, including the butterfly effect, is introduced as a sensitivity to initial conditions in deterministic systems.
- ⚫ The simple equation Z squared plus C is fundamental to both the Mandelbrot and Julia sets.
- 🔁 Iteration involves repeatedly calculating the function and feeding the result back into the equation.
- 📉 Positive values of Z less than one head towards zero, while values greater than one head towards infinity.
- 🔶 The Mandelbrot set includes values from -2 to 0.25 on the real number line, traditionally colored black.
- 🔴 For negative values of C, the behavior of orbits becomes more complex and sensitive to the value of C.
- 🌈 The coloring of the Mandelbrot set is based on how quickly a point's orbit escapes, with the outside area colored to represent this.
- 📊 The full Mandelbrot Set is two-dimensional, involving complex numbers and their behavior in the complex plane.
- 🔍 Zooming into the set reveals intricate patterns and mini-Mandelbrots, which are smaller copies of the set with different periods.
- 🧐 The Mandelbrot set, while not practically useful, provides insight into complex dynamics and chaos, captivating mathematicians.
Q & A
What is the Mandelbrot set?
-The Mandelbrot set is a type of shape known as a fractal, calculated in the complex number system. It is famous for its intricate and infinitely detailed boundary, which is composed of shapes and patterns that are self-similar at different scales.
How is the Mandelbrot set calculated?
-The Mandelbrot set is calculated using an iterative process. For each point on the complex plane, the equation Z squared plus C is computed, the result is assigned to the value of Z, and then this new value of Z is fed back into the equation repeatedly. If the value of Z remains bounded (does not go towards infinity), the point is considered part of the set.
What is the significance of the equation Z squared plus C?
-The equation Z squared plus C is significant because it is the formula used to calculate both the Mandelbrot set and the Julia sets, two closely related types of fractals. This simple equation exhibits complex and chaotic behavior, which is a key aspect of the Mandelbrot set's fascinating properties.
What is the butterfly effect in the context of the Mandelbrot set?
-In the context of the Mandelbrot set, the butterfly effect refers to the extreme sensitivity of the set's behavior to the initial conditions, similar to how small changes in a weather model can lead to vastly different outcomes. This concept is illustrated by how the value of C, even when slightly adjusted, can lead to dramatically different orbits of Z within the set's calculation.
What are the fixed points in the function Z squared?
-In the function Z squared, the fixed points are the values of Z that do not change with iteration. There are two such points: 0 and 1. The point 0 is an attractive fixed point because nearby orbits are attracted to it, while 1 is a repelling point because orbits near it move away.
How does the value of C affect the behavior of the Mandelbrot set?
-The value of C, known as the parameter, significantly affects the behavior of the Mandelbrot set. Different values of C result in different orbits of Z and thus different points being included or excluded from the set. The sensitivity of the orbits to the value of C introduces a level of unpredictability and complexity to the set's structure.
What are the real number values that are always part of the Mandelbrot set?
-On the real number line, the Mandelbrot set includes all the values from -2 to 0.25 inclusive. These values, when iterated, remain localized and do not escape towards infinity, thus they are traditionally colored black and considered part of the set.
How does the concept of chaos theory relate to the Mandelbrot set?
-Chaos theory relates to the Mandelbrot set through the concept of deterministic chaos, where the system's behavior is highly sensitive to initial conditions. The Mandelbrot set demonstrates this through the unpredictable and complex behavior of the orbits of Z for different values of C, even when those values are very close to each other.
What are complex numbers and how are they used in the calculation of the Mandelbrot set?
-Complex numbers are two-dimensional numbers that extend the real numbers by introducing the imaginary unit 'i', where i squared equals -1. They have a real part and an imaginary part. In the calculation of the Mandelbrot set, complex numbers allow the set to be mapped in two dimensions, with the real part corresponding to the horizontal axis and the imaginary part to the vertical axis.
What is the significance of the value 2 in the context of the Mandelbrot set's calculation?
-The value 2 is significant in the calculation of the Mandelbrot set because it serves as a boundary for determining whether a point's orbit remains bounded or escapes towards infinity. If during the iterative process the absolute value of Z exceeds 2, it is guaranteed to head towards infinity, and thus that point is not considered part of the set.
How are the colors in the graphical representation of the Mandelbrot set determined?
-The colors in the graphical representation of the Mandelbrot set are determined by the number of iterations it takes for the value of Z to escape, that is, to exceed an absolute value of 2. Points that do not escape after a certain number of iterations are colored based on how quickly they escaped, with points that never escape typically colored black.
What is a 'minibrot' and how is it related to the Mandelbrot set?
-A 'minibrot' or mini-Mandelbrot is a smaller, self-similar copy of the Mandelbrot set that appears within the main set. It is formed when the orbit of a point stabilizes in a way that mimics the behavior of the original set but on a smaller scale and potentially at a different period, such as every third iteration.
Outlines
🌀 Introduction to the Mandelbrot Set's Beauty and Complexity
The Mandelbrot set is introduced as an infinitely detailed mathematical object with fascinating shapes and patterns. The video aims to provide an intuitive understanding of its underlying mechanisms, using simple mathematics and visual explanations. It touches on the Mandelbrot set's status as a fractal within the complex number system and hints at the butterfly effect's role in its chaotic behavior. The iterative process of calculating the set is also introduced, along with the distinction between the set itself (black) and the colored area outside it.
🔢 Dynamics of the Mandelbrot Set and Fixed Points
This paragraph delves into the behavior of the Mandelbrot set's calculation, focusing on the concept of fixed points (0 and 1) and their properties (attractive and repelling). It also discusses the impact of negative numbers on the set's dynamics and the importance of the orbits' ultimate fate in determining the set's boundaries. The coloring of points outside the set is based on their escape velocity, and the process of calculating the set is reiterated with an emphasis on the parameter C and its role in the iterative function Z = Z^2 + C.
🚀 Orbit Behavior and the Mandelbrot Set's Boundaries
The discussion shifts to the behavior of orbits within the Mandelbrot set, highlighting the importance of the absolute value of two as a threshold for orbits escaping to infinity. The video presents a graphical representation of how orbits are contained within the -2 to +2 range and how this knowledge aids in computer programming and color generation for the set. The exploration of which points are inside the set based on their iteration behavior is also covered, revealing the sensitivity of the function to the value of C.
🎨 Expanding to Two Dimensions with Complex Numbers
The video script explains the transition from one-dimensional real numbers to two-dimensional complex numbers, which includes a brief review of complex numbers and their algebraic operations. It emphasizes the graphical representation of squaring a complex number and how it results in a rotation around the complex plane. The process of visualizing the full Mandelbrot Set with the inclusion of complex numbers is described, and the method for determining the color of a pixel based on the number of iterations until escape is detailed.
🔍 Exploring the Mandelbrot Set's Internal Structure
This paragraph investigates the internal structure of the Mandelbrot set, focusing on how orbits behave differently within the set, leading to various patterns and periods. It describes the main cardioid and circle's relationship with period 1 and period 2 orbits, respectively, and how the bulbs within the set are associated with different periods. The chaotic behavior near the edge of the set is also highlighted, drawing a connection to the butterfly effect and the challenges of simulating complex systems like weather.
🌐 Mini-Mandelbrots and Their Formation
The video concludes with an exploration of 'minibrots,' or mini-Mandelbrots, which are smaller, often imperfect copies of the Mandelbrot set that occur within the main set. It explains how these formations are a result of orbits stabilizing in a manner that mimics the original set's behavior, albeit at a smaller scale and potentially at different iteration intervals. The variety of minibrots and their relationship to the periods of the orbits is also discussed.
🔗 Conclusion and Future Exploration
The final paragraph wraps up the video with a summary of the insights gained about the Mandelbrot set and an invitation to join future explorations of related mathematical concepts, specifically the Julia Sets. It acknowledges the Mandelbrot set's lack of practical applications outside of computer graphics but emphasizes its significance in mathematical study. Links for further information are promised in the video description.
Mindmap
Keywords
💡Mandelbrot Set
💡Fractal
💡Complex Numbers
💡Iteration
💡Chaos Theory
💡Julia Sets
💡Attractive Fixed Point
💡Repelling Point
💡Orbit
💡Escape Radius
💡Mini-Mandelbrot
Highlights
The Mandelbrot set is a fractal with infinite shapes and patterns, calculated using complex numbers.
Exploration of the Mandelbrot set is usually part of a post-graduate complex dynamics course.
The set is visualized using a mostly visual explanation to build an intuitive understanding.
The black part of the Mandelbrot set represents the actual set, with colored areas outside it.
The Mandelbrot set is calculated by iterating the equation Z squared plus C.
Chaos theory and the butterfly effect are introduced through Edward Lorenz's weather modeling.
The simplest function exhibiting chaotic behavior is Z squared plus C, which is also the equation for the Mandelbrot set.
The process of iteration involves repeatedly calculating the function and feeding the result back into the equation.
Fixed points in the set, such as 0 and 1, represent values that do not change over iterations.
The ultimate fate of orbits (whether they escape to infinity or remain localized) is key to calculating the Mandelbrot set.
Values from -2 to 1 on the real number line that remain localized are part of the Mandelbrot set and are colored black.
The Mandelbrot set includes points where the orbit of Z under iteration never escapes, indicating a sensitive dependence on initial conditions.
Complex numbers extend the real number line to two dimensions, introducing the imaginary unit i, the square root of -1.
The full Mandelbrot Set is a two-dimensional map showing the behavior of Z for all possible complex values of C.
The coloring of the Mandelbrot set is determined by the number of iterations until Z escapes, producing beautiful patterns.
Minibrots are smaller, almost identical copies of the Mandelbrot Set that form due to the stabilization of orbits at particular locations.
The Mandelbrot set, while having no practical uses outside of computer graphics, is a subject of great interest to mathematicians for its complexity and beauty.
The video concludes with an invitation to explore Julia Sets in future videos and to understand their relationship to the Mandelbrot set.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: