Non-Euclidean Geometry Explained - Hyperbolica Devlog #1
TLDRThe video script delves into the fascinating world of hyperbolic space, contrasting it with the more familiar Euclidean and spherical geometries. It explains that while spherical space has positive curvature where lines always converge, hyperbolic space has negative curvature where lines always diverge. The script uses creative visualizations like hyperbolic crochet to illustrate how more squares can meet at a vertex in hyperbolic space. It also discusses the concept of holonomy, where movement in curved spaces results in unexpected rotations. The video further explores how the curvature affects the properties of circles and triangles, with unique formulas for calculating their circumferences and areas. Finally, it highlights the use of stereographic projection as a tool to visualize these complex geometries, and ends with a teaser for the next video, which will explore three-dimensional curved spaces and their mathematical underpinnings.
Takeaways
- 📐 **Hyperbolic Space Visualization**: The script introduces a new way to understand hyperbolic space by first looking at Euclidean and spherical spaces in two dimensions, then transitioning to hyperbolic space in three dimensions.
- 🌐 **Spherical vs. Hyperbolic Geometry**: In spherical geometry, fewer squares can meet at a vertex compared to Euclidean space, whereas in hyperbolic space, more squares can meet at a vertex.
- 🧵 **Hyperbolic Crochet**: A physical model called 'hyperbolic crochet' is used to visualize how five squares can meet at every vertex in hyperbolic space.
- 🌍 **Spherical Curvature**: The script explains that if Earth had a spherical space-time, light would travel around the Earth, eliminating the concept of a horizon.
- 🔍 **Tiling and Curvature**: The way regular polygons can tile a plane differs in Euclidean, spherical, and hyperbolic spaces due to curvature.
- 🌀 **Projection Techniques**: To visualize the hyperbolic plane, the script discusses the use of projection techniques such as stereographic projection, which can distort angles and distances.
- 🔄 **Parallel Lines**: In spherical geometry, all lines converge, whereas in hyperbolic geometry, lines always diverge.
- 🚶 **Holonomy**: The script introduces the concept of 'holonomy', where movement in curved spaces can result in unexpected rotations of the observer's view.
- 🧲 **Tidal Forces**: Objects in spherical geometry experience a squishing force, while in hyperbolic geometry, they experience a stretching force.
- ⭕ **Circle Circumference**: The circumference of a circle in spherical space is given by 2π sin(r), which contrasts with the Euclidean formula and reflects the cyclic nature of distances in spherical geometry.
- 🔢 **Area Formulas**: The area of a circle in hyperbolic space grows exponentially with the radius, and there's a unique formula for the area of a triangle based on its angles in both spherical and hyperbolic spaces.
Q & A
What is the main issue with visualizing hyperbolic space using traditional methods?
-Traditional methods often fail to convey the true experience of living in a curved space, which is why the creator started Hyperbolica to find an easier way to understand hyperbolic space.
How does the concept of a spherical shell differ from our perception of Earth's surface?
-While Earth's surface may seem similar to a spherical shell, the key difference lies in how light travels. If Earth had a spherical space-time, light would travel all the way around the Earth, eliminating the concept of a horizon.
What are the three ways to tile the Euclidean plane with regular polygons?
-The three ways are: 4 squares at a vertex, 6 triangles at a vertex, or 3 hexagons at a vertex.
How does tiling with pentagons differ from the three accepted methods in Euclidean geometry?
-Tiling with pentagons is not possible in Euclidean geometry because there's not enough space for four pentagons and too much gap for three to meet at a vertex.
What is the fundamental difference between spherical and hyperbolic geometry when it comes to tiling with squares?
-In spherical geometry, fewer squares can meet at a vertex compared to Euclidean space, whereas in hyperbolic space, more squares can meet at a vertex.
How does hyperbolic crochet, as shown in the video, help visualize the hyperbolic space?
-Hyperbolic crochet, created by Mrs. Parade, visually demonstrates how five squares can meet at every vertex in hyperbolic space, providing a tangible model of the geometry.
Why is it difficult to visualize the entirety of hyperbolic space even with a 3D model?
-Flattening one area of the hyperbolic space in a 3D model causes other areas to start curving, making it impossible to see the entire space at once due to the nature of the curvature.
What is the trick used to visualize the hyperbolic plane when direct 3D models are insufficient?
-Projection is used as a method to visualize the hyperbolic plane. This involves projecting a curved geometry onto a flat surface, similar to how a 3D object is projected onto a 2D screen.
How does stereographic projection help in visualizing spherical and hyperbolic spaces?
-Stereographic projection allows for the visualization of curved geometries on a flat plane by using light and shadows, which can help understand the properties of these spaces without the distortions inherent in other types of projections.
What is the concept of 'Holonomy' in the context of spherical and hyperbolic geometry?
-Holonomy is the accumulation of extra rotation as you move around the space, even if you never change the direction you're facing. It's an effect not experienced in Euclidean geometry and results in a rotation upon returning to the starting point after a walk in curved spaces.
How does the movement of particles in an object affect its experience of tidal forces in spherical and hyperbolic geometries?
-In spherical geometry, the lack of parallel lines means objects experience a 'squishing' tidal force, similar to spaghettification around a black hole. Conversely, in hyperbolic space, objects experience a 'stretching' tidal force due to the divergence of lines.
What are the formulas for the circumference and area of a circle in spherical and hyperbolic spaces?
-In spherical space, the circumference is 2π sin(r), and the area grows cyclically with radius. In hyperbolic space, the circumference is given by the hyperbolic sine function, and the area grows exponentially at the same rate as the circumference.
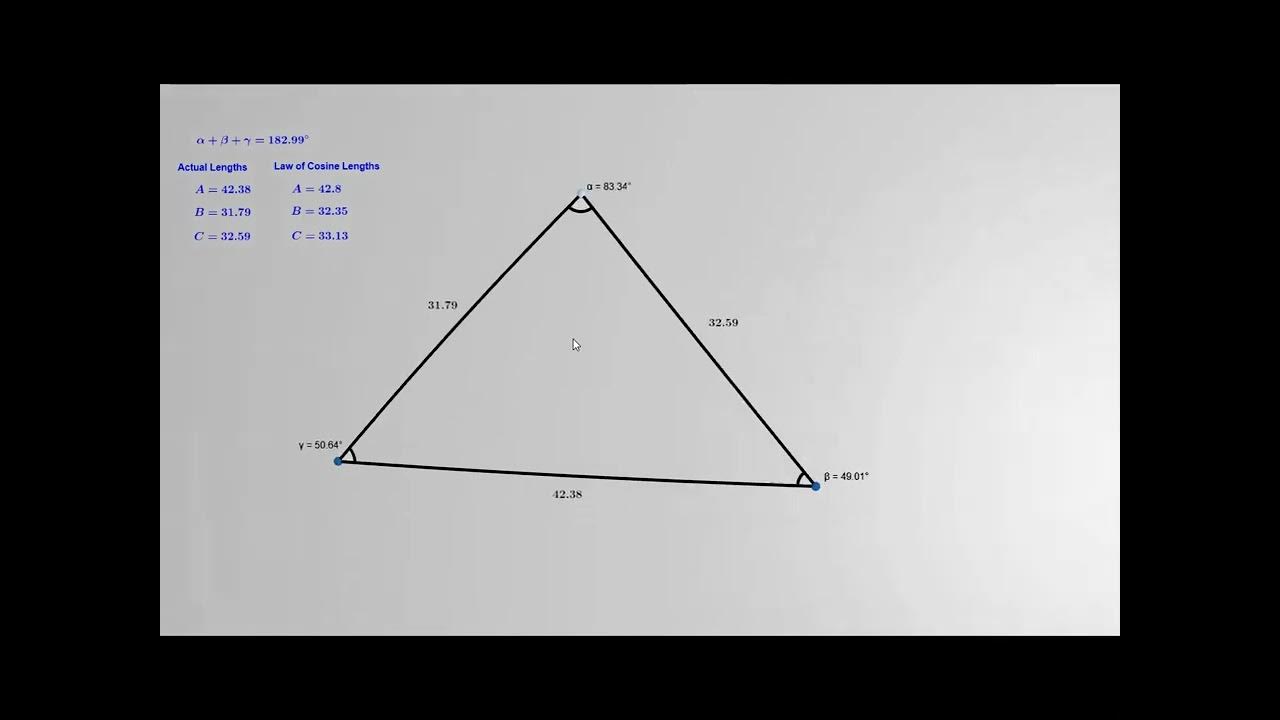
What is the unique formula for finding the area of a triangle in a unit curved space, and how does it differ between spherical and hyperbolic spaces?
-In a unit curved space, the area of a triangle can be found using the sum of its angles. For spherical space, the formula is the sum of the angles minus Pi, and for hyperbolic space, it's Pi minus the sum of the angles. This reflects the maximum possible area a triangle can have in hyperbolic space when all angles are zero degrees.
Outlines
🌐 Understanding Hyperbolic Space
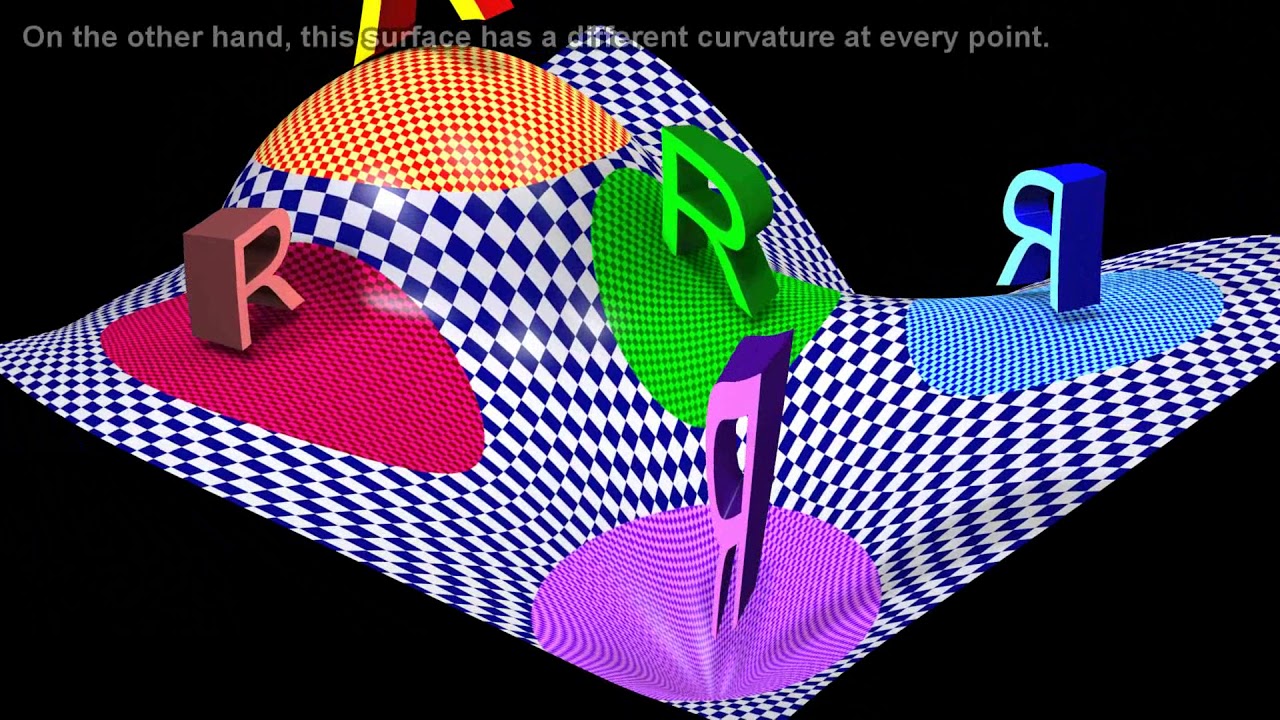
The first paragraph introduces the concept of hyperbolic space and the challenges in visualizing it. The speaker shares their motivation for starting Hyperbolica, an initiative to make hyperbolic space more understandable. The paragraph begins with a comparison of Euclidean and spherical spaces in two dimensions and suggests that understanding these will naturally lead to an understanding of hyperbolic space in three dimensions. It explains the Euclidean plane as flat and unending with no curvature, contrasting it with a spherical shell that, despite being a two-dimensional surface, has positive curvature. The paragraph also touches on how light behaves in a curved space, like a black hole, and how this affects the perception of distance and direction. Tiling with regular polygons is used to illustrate the differences between Euclidean and spherical geometries. The transition to hyperbolic space is introduced with the concept that, unlike spherical geometry, hyperbolic space allows for more squares to meet at a vertex. The paragraph concludes with the idea that to fully grasp hyperbolic space, a different visualization technique, such as projection, is necessary.
🌟 Exploring Spherical and Hyperbolic Geometries
The second paragraph delves into the properties of spherical and hyperbolic geometries, focusing on the concept of parallel lines and their absence in spherical geometry. It explains that in spherical space, all lines eventually converge, whereas in hyperbolic space, they always diverge. The speaker uses the analogy of walking on a sphere and a hyperbolic plane to illustrate the differences in geometry, highlighting the phenomenon of 'Holonomy' where movement through the space results in unexpected rotation. The paragraph also discusses the physical implications of moving objects in curved spaces, with spherical geometry causing a 'squishing' effect and hyperbolic geometry causing a 'stretching' effect. Formulas for the circumference and area of circles in spherical and hyperbolic spaces are introduced, emphasizing the exponential growth in hyperbolic space. The Pythagorean theorem and its curved space analogues are briefly mentioned, and a unique formula for finding the area of a triangle in a unit curved space using only its angles is presented, with a simple formula for spherical and hyperbolic spaces.
📐 Mathematical Insights into Curved Spaces
The third paragraph provides further mathematical insight into the properties of triangles in curved spaces. It explains that in hyperbolic space, the sum of the angles of a triangle is always less than 180 degrees, leading to a maximum possible area for a triangle when all angles are zero. The speaker anticipates the next video, which will discuss three-dimensional spaces, rendering techniques in Unity, and the underlying mathematics. The paragraph concludes with a recommendation for the game HyperRogue as a way to build more intuition about hyperbolic space and an invitation to the audience to continue exploring the topic.
Mindmap
Keywords
💡Hyperbolic space
💡Euclidean plane
💡Spherical space
💡Tiling
💡Stereographic projection
💡Parallel lines
💡Holonomy
💡Tidal force
💡Circumference and area formulas
💡Pythagorean theorem
💡Triangle area formula
Highlights
Hyperbolic space visualizations are often misunderstood, leading to the creation of Hyperbolica for better understanding.
Euclidean, spherical, and hyperbolic spaces are introduced starting from two-dimensional perspectives before moving to three dimensions.
Spherical space is an infinitely thin two-dimensional shell, unlike a solid ball, and is visualized from a higher dimension.
Light behaves differently in curved spaces, always traveling the shortest path which can bend around phenomena like black holes.
Tiling patterns in spherical geometry can accommodate more polygons around a vertex due to curvature, unlike Euclidean geometry.
Hyperbolic geometry allows for more squares around a vertex compared to Euclidean space, demonstrated through hyperbolic crochet.
Visualization of hyperbolic space is challenging and often requires the use of an extra dimension to comprehend the curvature.
Projection methods, such as stereographic projection, are used to translate curved geometries onto flat planes for visualization.
Different projections introduce various distortions in distances, angles, areas, or shapes, depending on the application.
Parallel lines do not exist in spherical geometry; all lines converge and intersect, a local rather than global property.
In hyperbolic space, lines diverge, contrasting with spherical geometry where they converge.
Spherical geometry introduces a 'Holonomy' effect, where movement results in an accumulated rotation without changing view direction.
Hyperbolic space exhibits a stretching tidal force on objects in motion, as opposed to the squishing force in spherical geometry.
The circumference and area of a circle in spherical and hyperbolic spaces are calculated differently from Euclidean space, with unique formulas.
The Pythagorean theorem has beautiful analogues in curved spaces, adapting to the geometry of the space.
A unique formula in unit curved spaces allows finding the area of a triangle using only its angles, with a simple expression.
In hyperbolic space, there's a maximum possible area for a triangle due to the divergence of lines, which is when all angles are zero degrees.
The video concludes with a teaser for the next video about three-dimensional spaces, rendering techniques in Unity, and further exploration of the math behind it.
HyperRogue, a hyperbolic game, is recommended for building more intuition about hyperbolic space.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: