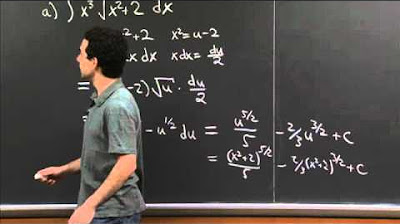Integration by substitution
TLDRIn this video, Sarah from Selfish Maths dives into the concept of integration by substitution, a method for solving complex integrals. She begins with three examples of indefinite integration, guiding viewers through the process of choosing a substitution based on the most complex expression in the integral. Sarah then demonstrates how to differentiate the substitution and rearrange the equation to facilitate the integration process. She emphasizes the importance of substituting back to the original variable after integration. Following the indefinite integration examples, Sarah tackles two examples of definite integration, highlighting the need to adjust the limits of integration when substituting. Throughout the video, she encourages viewers to practice and pause the video to work through the examples themselves. Sarah's approachable teaching style and clear explanations make this video an excellent resource for those looking to understand and practice integration by substitution.
Takeaways
- 📚 Start with understanding the basics of integration and differentiation before diving into integration by substitution.
- 🔍 Look for the most complex expression in the integral to guide your substitution choice, often indicated by the question itself.
- ✍️ Differentiate the substitution expression to find du/dx, then rearrange to express dx in terms of du.
- 🔄 Substitute dx with du/dx expression in the integral, simplifying the integral for easier computation.
- 🧮 Practice using the reverse chain rule and double angle formulas to integrate more complex expressions.
- 📈 Integrate by substitution even when not explicitly told to do so, as it can simplify the integral and make it solvable.
- 📐 Use trigonometric identities and logarithmic properties to simplify expressions before integrating.
- 🔗 When dealing with definite integrals, remember to change the limits according to the substitution made.
- ➡️ When switching the order of limits in a definite integral, include a negative sign to account for the reversal.
- 📊 Practice is key for mastering integration by substitution; continue to apply it to various problems for better understanding.
- 🎓 For a deeper understanding, watch additional videos on related topics such as reverse chain rule and double angle formulas.
Q & A
What mathematical concept is the video primarily focused on?
-The video is primarily focused on integration by substitution.
How does the speaker suggest viewers approach the examples provided in the video?
-The speaker suggests viewers grab a pen and paper, do the work themselves, and pause or rewind the video as needed.
What substitution does the speaker suggest using for the first example?
-For the first example, the speaker suggests using the denominator expression, 2x^3 - 1, as the substitution.
What is the first step in integration by substitution after choosing the substitution?
-The first step is to differentiate the chosen substitution expression.
In the second example, what substitution does the speaker recommend?
-In the second example, the speaker recommends making the denominator expression, sine 2x, the substitution.
How does the speaker handle the substitution of sine 2x in the second example?
-The speaker expands sine 2x as 2sin(x)cos(x) and then substitutes it into the expression.
What is the approach suggested by the speaker for handling complex-looking integrals?
-The speaker advises trying different substitutions until something works and mentions that there are often multiple ways to integrate expressions.
How does the speaker handle definite integration with substitution?
-For definite integration with substitution, the speaker reminds viewers to change the limits accordingly when substituting and to be mindful of the change in sign when rearranging limits.
What happens to the limits when performing definite integration with substitution?
-The limits are replaced with the corresponding limits in terms of the substitution variable, and there is a change in sign if the order of the limits is reversed.
What is emphasized as essential for mastering integration by substitution?
-The speaker emphasizes the importance of practicing integration by substitution regularly to gain proficiency.
Outlines
😀 Introduction to Integration by Substitution
Sarah introduces integration by substitution in this video. She emphasizes its relevance to topics such as integration and differentiation. The video covers three examples of indefinite integration and two examples of definite integration. Sarah encourages viewers to actively engage by practicing alongside the video.
😊 Example 1: Integration Using Reverse Chain Rule
Sarah presents an example of integration by substitution using the reverse chain rule. While she doesn't demonstrate it, she encourages viewers to practice integrating the expression. Instead, she introduces an alternative method: integration by substitution. She explains the process of selecting the appropriate substitution and demonstrates the steps involved in integrating the expression.
📐 Example 2: Trigonometric Integration
In this example, Sarah tackles a trigonometric integration problem. She chooses the denominator as the substitution and guides viewers through the differentiation process to find the substitution for DX. Sarah expands the trigonometric expression and simplifies it before integrating. She provides detailed steps on handling the fraction and integrating with respect to 'u' to arrive at the final solution.
📚 Example 3: Integration with Logarithms
Sarah presents an example involving logarithmic integration, explaining that it's a good candidate for substitution due to its complexity. She chooses 'u' as the substitution and demonstrates the differentiation process. The expression is then split into fractions for easier integration. Sarah integrates each term separately and substitutes back to obtain the final result.
🔢 Definite Integration: Changing Limits
Sarah demonstrates definite integration by substitution, highlighting the need to change limits accordingly. She substitutes the given expression and changes the limits from X to 'u'. Sarah carefully adjusts the limits, ensuring their correctness, and integrates the expression. She concludes by factoring and providing the solution, emphasizing the importance of correctly handling limits.
📝 Conclusion and Recap
Sarah concludes the video by summarizing the topics covered: integration by substitution with examples of indefinite and definite integrals. She encourages viewers to practice more and emphasizes the importance of familiarity with the method. Sarah expresses gratitude to the audience for watching and encourages them to continue learning and having fun with integration.
Mindmap
Keywords
💡Integration by Substitution
💡Reverse Chain Rule
💡Definite Integration
💡Indefinite Integration
💡Double Angle
💡Trigonometric Substitution
💡Natural Logarithm
💡Exponential Function
💡Limits
💡Constant of Integration
💡Differentiation
Highlights
Integration by substitution is introduced as an alternative method to the reverse chain rule for integrating complex expressions.
The video begins with three examples of indefinite integration, followed by two examples of definite integration using limits.
The first example uses the reverse chain rule and substitution with the denominator 2x^3 - 1, leading to a simplified integration process.
The substitution method often involves the most complex expression in the integral, which is used to define the substitution variable 'u'.
Differentiating the substitution expression and rearranging to solve for dx/du is a key step in the process.
Substitution can lead to cancellation of terms, simplifying the integral, as demonstrated in the first example where x^2 terms cancel out.
The second example involves trigonometric functions, using a double angle formula to simplify the integral before substitution.
The video emphasizes the importance of practice in recognizing when to use substitution and the types of expressions it can simplify.
The third example demonstrates the use of substitution with logarithmic functions, which cannot be integrated using the reverse chain rule.
Definite integration examples are presented with a focus on changing the limits according to the substitution variable.
Changing the order of integration limits introduces a change of sign in the integral, which is accounted for in the calculation.
The final definite integration example involves a complex expression that simplifies significantly after applying substitution.
The video concludes with a reminder of the importance of practice and offers encouragement for further study and application of integration by substitution.
Sarah, the presenter, encourages viewers to pause the video and work through the examples themselves to enhance understanding.
The process of substituting dx with du/(6x^2) is detailed, showing how to directly substitute into the integral for simplification.
The substitution method is shown to be effective in transforming complex integrals into more manageable forms for easier integration.
The video provides a step-by-step guide to integrating e^u, factorizing, and handling limits in definite integration.
Sarah emphasizes the utility of substitution in simplifying the integration of expressions involving trigonometric, logarithmic, and exponential functions.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: