Divisibility Rules

D!NG

19 Mar 202024:32

EducationalLearning

32 Likes 10 Comments

TLDRThe video script features a detailed exploration of divisibility rules for the numbers 1 through 9, providing entertaining and educational content on how to determine if one number can be evenly divided by another without a remainder. The host, Michael, emphasizes the importance of developing number sense and making math friends during these times. He explains various tricks, such as summing digits for divisibility by 3, checking the last two digits for divisibility by 4, and a unique method involving multiplication by 5 and subtraction for divisibility by 7. The script also delves into the mathematical reasoning behind these tricks, enhancing the viewer's understanding. Additionally, the video includes a segment on a historical puzzle invented by Theodore Edison, the 'Caliber on 12,' which adds an interactive element to the content. The script concludes with a message from the sponsor, Vsauce, highlighting the benefits of curiosity and the positive impact of supporting their cause, including contributions to Alzheimer's research.

Takeaways

🔢 The importance of practicing responsible social distancing is emphasized, especially during challenging times, to promote unity.
🤔 Divisibility rules for numbers 1 through 9 can be fun and help develop number sense, offering an alternative to using a calculator or asking Google.
👌 A number is divisible by 1 if it's an integer, by 2 if it's even, and by 5 if it ends in 0 or 5.
🤓 For divisibility by 3, sum the digits of the number; if the sum is divisible by 3, so is the number.
🧮 To check for divisibility by 4, ensure the last two digits form a number that is divisible by 4.
📐 A number is divisible by 6 if it is divisible by both 3 and 2.
🎲 For divisibility by 8, consider the last three digits of the number and apply a specific multiplication and addition rule.
🔍 Divisibility by 9 works similarly to that by 3, where the sum of the digits is checked for divisibility by 9.
🔧 The divisibility rule for 7 involves multiplying the ones digit by 5 and adding it to the remaining number, then checking for divisibility by 7.
🧠 The script explains the mathematical reasoning behind the divisibility rules, showing how they are derived from the base-10 positional system.
🧩 The video concludes with a mention of a puzzle called the 'Caliber on 12' invented by Theodore Edison, which comes with multiple variations and supports Alzheimer's research through the Curiosity Box.

Q & A

What is the importance of practicing social distancing mentioned in the transcript?
-The importance of practicing social distancing is emphasized as a crucial part of everyone's responsibility during times of a pandemic or health crisis, highlighting the need for unity in taking preventive measures.
How can one quickly determine if a number is divisible by 2 or 5?
-A number is divisible by 2 if it is even, and by 5 if it ends in a zero or five, without leaving any remainder.
What is the trick for checking divisibility by 3?
-The trick for checking divisibility by 3 involves summing all the digits of the given number. If the sum is divisible by 3, so is the original number.
How does the divisibility rule for 4 work?
-A number is divisible by 4 if the last two digits of the number form a number that is divisible by 4. One can also double the tens digit and add it to the ones digit; if the sum is divisible by 4, so is the original number.
What is the process for checking if a number is divisible by 8?
-To check for divisibility by 8, one must consider the last three digits of the number. Multiply the hundreds digit by 4, add twice the tens digit, and then add the ones digit. If the sum is divisible by 8, the original number is as well.
What is the trick for divisibility by 7?
-The trick for divisibility by 7 involves taking the ones digit of the number, multiplying it by 5, and then adding that product to the remaining digits of the number. If the resulting sum is divisible by 7, so is the original number.
Why does the divisibility trick for 3 work?
-The trick works because when you sum the digits of a number, you are essentially checking if the sum, which is composed of multiples of 3 (since each digit represents a power of 10, and 10 is 9 plus 1, both of which are multiples of 3), is divisible by 3. If the sum is divisible, so is the number.
What is the significance of the number 3602880 in the transcript?
-The number 3602880 is significant because it is nine factorial, meaning it is the product of all positive integers from 1 to 9. As a result, it is a multiple of every number from 1 to 9, making it divisible by all these numbers.
How does the divisibility rule for 6 relate to the rules for 3 and 2?
-A number is divisible by 6 if it is divisible by both 3 and 2. This is because 6 is the product of 3 and 2, so a number must be even (divisible by 2) and have a sum of digits divisible by 3 to be divisible by 6.
What is the purpose of developing number sense through these divisibility rules?
-Developing number sense through these divisibility rules helps individuals to better understand the properties of numbers and how they relate to one another, enhancing their mathematical intuition and problem-solving skills.
What is the connection between the Vsauce Curiosity Box and Alzheimer's research?
-A portion of the proceeds from the Vsauce Curiosity Box is donated to Alzheimer's research. This initiative has allowed them to contribute over $100,000 to this cause, highlighting the box's significance beyond its educational value.

Outlines

00:00

🔢 Divisibility Rules: Fun with Numbers

Michael introduces the topic of divisibility rules, emphasizing the importance of social distancing and unity during challenging times. He explains that while calculators and Google can quickly determine if a number is divisible by another, learning these rules helps develop number sense and can be a fun way to make math friends. The paragraph covers basic divisibility rules for numbers 1 through 5 and introduces a trick for divisibility by 3, using the sum of a number's digits. An example is given with the number 360,2880 to illustrate the process.

05:03

🤔 Tricks for Divisibility by 6, 8, and 9

The paragraph delves into divisibility by 6, 8, and 9. It explains that a number is divisible by 6 if it is divisible by both 3 and 2. For divisibility by 4, a trick is introduced involving the last two digits of a number. The concept is further explored for divisibility by 8, where the last three digits are considered, using a formula involving the hundreds, tens, and ones digits. The paragraph concludes with a teaser for the upcoming discussion on divisibility by 7.

10:04

🤓 Divisibility by 7: A Repeated Process

Michael presents a method for determining if a number is divisible by 7, which involves multiplying the ones digit by 5 and adding it to the remaining number. The example of 350,2880 is used to demonstrate this process, which may need to be repeated until a recognizable pattern emerges. The paragraph reveals that 360,2880 is a multiple of all numbers up to 9, being nine factorial, and thus divisible by 7. The process is shown step by step, emphasizing the need for repetition until a divisible number by 7 is reached.

15:06

🧮 The Mathematical Basis of Divisibility Tricks

This paragraph explores the mathematical reasoning behind the divisibility tricks for numbers 3 and 4. It explains why the sum of the digits of a number is divisible by 3 if the number itself is, and why the last two digits of a number determine its divisibility by 4. The concept is generalized for a three-digit number, showing how the sum of the digits relates to the actual value of the number in a base-10 system. The paragraph provides a deeper understanding of why these tricks work and how they can be applied to numbers with any number of digits.

20:10

🧩 Divisibility by 7 and the Caliber on 12 Puzzle

The final paragraph discusses the peculiar trick for divisibility by 7 and provides a mathematical explanation for why it works. It involves algebraic manipulation to show that the expression used for the divisibility check is equivalent to the original number, thus if the transformed expression is divisible by 7, so is the original number. The paragraph concludes with a message from the sponsor, Vsauce, and a description of the Curiosity Box, which includes a replica of the 'Caliber on 12' puzzle invented by Theodore Edison. The proceeds from the box support Alzheimer's research, and the presenter thanks the viewers for their support and curiosity.

Mindmap

Keywords

💡Divisibility Rules

Divisibility rules are mathematical methods that allow us to determine whether a number can be evenly divided by another number without leaving a remainder. In the video, these rules are used to explore and demonstrate how to quickly determine if a number is divisible by the numbers 1 through 9, which is central to the video's theme of mathematical fun and number sense development.

💡Number Sense

Number sense refers to an individual's intuitive understanding of numbers, their relationships, and properties. The video emphasizes developing number sense through engaging with divisibility rules, which helps in understanding the underlying patterns and characteristics of numbers beyond just computational efficiency.

💡Social Distancing

Social distancing is a public health practice that involves maintaining a safe physical distance between people to prevent the spread of infectious diseases. The video begins with a reference to practicing social distancing, highlighting the importance of community health and safety during times of crisis, which is a significant theme given the context of the video's release.

💡Calculator

A calculator is an electronic device used to perform arithmetic operations. The video contrasts the use of calculators for speed with the enjoyment and educational value of manual divisibility checks, emphasizing the importance of mathematical understanding over mere computational speed.

💡Nine Factorial

Nine factorial, written as 9!, is the product of all positive integers from 1 to 9. In the video, the number 3602880 is identified as nine factorial, which is relevant because it is a multiple of all the numbers from 1 to 9, making it a useful example when demonstrating divisibility rules.

💡Summation of Digits

The summation of digits is a technique used in several divisibility rules, such as for numbers 3 and 9, where the sum of a number's digits is considered to determine divisibility. The video explains that if the sum of the digits is divisible by 3, then the original number is also divisible by 3, showcasing this technique with the example number 3602880.

💡Even Numbers

Even numbers are integers that are divisible by 2. The video mentions that any integer can be divided into groups of one, and if it's even, it's divisible by two, which is a fundamental concept in the divisibility rule for the number 2.

💡Divisibility by Four

Divisibility by four is determined by examining the last two digits of a number. If those two digits form a number divisible by four, then the entire number is divisible by four. The video provides a trick for this by doubling the tens digit and adding the ones digit, using this method to demonstrate the divisibility of numbers like 80 and 96.

💡Divisibility by Eight

Divisibility by eight involves looking at the last three digits of a number. The video explains a method where you multiply the hundreds digit by four, add twice the tens digit, and then add the ones digit. If this sum is divisible by 8, so is the original number, as illustrated with the number 3602880.

💡Divisibility by Seven

Divisibility by seven is checked using a unique trick where you multiply the ones digit by five and add it to the remaining number after removing the ones digit. The video demonstrates this with the number 3602880, showing that if the resulting number is divisible by seven, so is the original number.

💡Curiosity Box

The Curiosity Box is a subscription box mentioned in the video that includes items designed to stimulate curiosity and intellectual engagement. The video discusses a specific puzzle from the box, the caliber on 12, invented by Theodore Edison, which is a physical puzzle that adds a hands-on element to the theme of exploring and understanding mathematical and logical concepts.

Highlights

The importance of practicing responsible social distancing during times of crisis is emphasized.

Divisibility rules for numbers 1 through 9 are introduced as a fun and engaging way to develop number sense.

A trick for divisibility by 3 is explained, involving summing the digits of a number.

The divisibility rule for 9 is similar to that of 3, using the sum of the digits.

For divisibility by 6, a number must be divisible by both 3 and be an even number.

A method for checking divisibility by 4 is presented, focusing on the last two digits of a number.

An alternative trick for divisibility by 4 is shared, involving doubling the tens digit and adding the ones digit.

The divisibility by 8 is checked by examining the last three digits of a number.

A unique trick for divisibility by 7 is demonstrated, involving multiplying the ones digit by 5 and adding it to the rest of the number.

The mathematical reasoning behind the divisibility rule for 3 is explained using base-10 positional system.

Similar logic is applied to explain the divisibility rule for 4, focusing on the last two digits.

An explanation of the divisibility rule for 8 is provided, considering the last three digits and their mathematical relationship.

The divisibility trick for 7 is mathematically justified, showing how it relates to the number 49, which is divisible by 7.

The purpose of these exercises is not speed but to enhance number sense and appreciation for numbers.

A historical note on the 'Caliber on 12' puzzle invented by Theodore Edison is shared.

The Curiosity Box includes a replica of the 'Caliber on 12' puzzle, with additional challenges compared to the original.

Proceeds from the Curiosity Box contribute to Alzheimer's research, with over $100,000 donated so far.

The benefits of engaging with puzzles and mathematical problems for brain health are highlighted.

Transcripts

Browse More Related Video

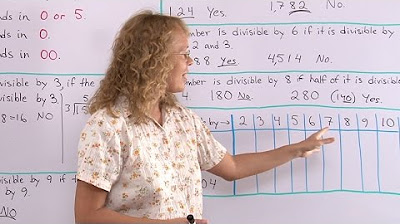
Divisibility rules for 3, 4, 6, 8 and 9

This completely changed the way I see numbers | Modular Arithmetic Visually Explained

Why is a Circle 360 Degrees, Why Not a Simpler Number, like 100?

How to EASILY Improve Your Mental Maths | 8 Simple Tricks

You, me, and my first International Math Olympiad problem

An "unsolvable" logic puzzle

Related Tags

Divisibility Rules Number Sense Vsauce Michael Stevens Math Tricks Social Distancing Puzzle Solving Caliber on 12 Edison Puzzle Alzheimer's Research Curiosity Box