Integration Practice III | MIT 18.01SC Single Variable Calculus, Fall 2010

MIT OpenCourseWare
7 Jan 201112:25
EducationalLearning
32 Likes 10 Comments

TLDRIn this educational video, the instructor tackles two complex integral problems, guiding viewers through the process of selecting the appropriate technique for each. For the first indefinite integral involving a product of x cubed and the square root of x squared plus 2, the instructor opts for a substitution method, simplifying the problem and avoiding the need for integration by parts or trigonometric substitution. The second definite integral, involving x squared times the natural logarithm squared, is approached with integration by parts, effectively reducing the complexity of the integrand and leading to a final answer. The video serves as an insightful tutorial for those looking to improve their calculus skills.

Takeaways
  • 📚 Discusses different integration techniques with examples.
  • 🧮 Example A: Indefinite integral of x³√(x² + 2) dx.
  • 🔍 Explores potential methods: trig substitution, integration by parts, and regular substitution.
  • ✅ Chooses regular substitution for simplicity: u = x² + 2.
  • 🔄 Transforms the integral and simplifies: u - 2)√u du/2.
  • ✍️ Integrates and substitutes back: (x² + 2)^(5/2)/5 - 2/3 (x² + 2)^(3/2) + C.
  • 📝 Example B: Definite integral from 1 to e of x² ln(x²) dx.
  • 🔧 Considers regular substitution and integration by parts, chooses the latter.
  • 📈 Sets u = ln(x²) and v' = x², differentiates and integrates accordingly.
  • 🔁 Continues integration by parts on simplified integral, resulting in: 5e³/27 - 2/27.
Q & A

  • What are the two integrals discussed in the script?

    -The first integral is an indefinite integral of x cubed times the square root of (x squared plus 2) dx. The second integral is a definite integral from 1 to e of x squared times the natural logarithm of x squared with respect to x.

  • What technique is suggested for the first integral in the script?

    -A regular substitution is suggested for the first integral, setting u equal to x squared plus 2, which simplifies the integral into a sum of powers of u.

  • Why is a regular substitution preferred over trigonometric substitution for the first integral?

    -A regular substitution is preferred because it is simpler and quicker to apply, and it can often be used in conjunction with integration by parts if necessary. Trigonometric substitutions are generally more complicated and should be considered if simpler methods do not work.

  • What is the result of the substitution for the first integral?

    -After substitution, the integral becomes the integral of (u to the 3/2 over 2) minus (u to the 1/2) du, which simplifies to an antiderivative of a sum of powers of u.

  • What is the final form of the first integral after simplification?

    -The final form of the first integral is (u to the 5/2) divided by 5, minus (2/3) times (u to the 3/2), with a constant added at the end after back-substituting u with x squared plus 2.

  • What are the potential methods for solving the second integral discussed in the script?

    -The potential methods for solving the second integral include a regular substitution with u equals ln of x, or using integration by parts directly on the product form of the integral.

  • Why is integration by parts chosen over a regular substitution for the second integral?

    -Integration by parts is chosen because it simplifies the integrand from a polynomial times a function of the logarithm to a polynomial times an exponential, which is easier to integrate.

  • What is the first step in the integration by parts process for the second integral?

    -The first step is to choose u as ln x squared and v prime as x squared, then differentiate u to get u prime and integrate v prime to get v.

  • What is the result of the first integration by parts for the second integral?

    -The result is x cubed over 3 times ln x squared minus the integral of 2/3 times x squared ln x dx, which simplifies the integrand and allows for further integration by parts.

  • What is the final answer for the second integral after all steps are completed?

    -The final answer for the second integral is 5 e cubed over 27 minus 2 over 27, after evaluating the definite integral and simplifying the result.

  • What is the significance of the constant term in the indefinite integral solution?

    -The constant term is significant because it represents the arbitrary constant of integration, which is a necessary part of the solution to any indefinite integral.

  • Why is it important to evaluate the definite integral at the limits of integration?

    -Evaluating the definite integral at the limits of integration is important because it gives the net area under the curve between those limits, which is the actual value of the definite integral.

  • What is the role of the chain rule in differentiating ln x squared in the second integral?

    -The chain rule is used to differentiate ln x squared to get 2 ln x times the derivative of ln x, which is 1 over x, simplifying the integrand for integration by parts.

  • How does the script suggest simplifying the integrand of the second integral after the first integration by parts?

    -The script suggests further integrating by parts, taking u as ln x and v prime as x squared, to simplify the integrand to a form that is easier to integrate directly.

Outlines
00:00
📚 Introduction to Integral Computation Techniques

The video script begins with an introduction to various integration techniques, presenting two integral problems for the viewer to solve. The first is an indefinite integral involving a product of x cubed and the square root of a quadratic expression, while the second is a definite integral with a product of a quadratic expression and a logarithmic function. The instructor encourages the viewer to attempt the problems before continuing with the solutions, emphasizing the importance of choosing the right technique for each integral.

05:02
🔍 Detailed Solution for the First Integral Problem

The instructor proceeds to solve the first integral by rewriting it and considering different approaches, such as trigonometric substitution, integration by parts, or a regular substitution. After evaluating the options, the instructor opts for a regular substitution, setting u equal to the quadratic expression under the square root. This leads to a simpler integral in terms of u, which is then solved by recognizing it as a sum of powers of u. The solution involves basic integration and back-substitution to express the final result in terms of the original variable x, along with the addition of a constant for an indefinite integral.

10:04
🧩 Solving the Second Integral Using Integration by Parts

For the second integral, the instructor discusses the possibility of using a regular substitution or integration by parts due to the product form of the integrand. After considering the complexity of differentiating polynomials versus logarithms, the instructor decides to use integration by parts directly. The function with the logarithm is chosen for differentiation, simplifying the integrand to a form that can be further integrated by parts if necessary. The definite integral is evaluated by taking the difference of the simplified integrand at the bounds of integration, resulting in a constant. The process is repeated, leading to a final integral that is a polynomial, which is straightforward to integrate. The instructor leaves the final steps to the viewer, with a hint at the final answer involving powers of e.

Mindmap
Keywords
💡Integration Techniques
Integration techniques refer to various methods used to evaluate integrals in calculus. In the video, the theme revolves around different strategies for solving integrals, such as substitution and integration by parts. The script mentions these techniques in the context of tackling two specific integral problems, emphasizing the importance of choosing the right technique for each scenario.
💡Indefinite Integral
An indefinite integral represents the family of antiderivatives of a given function. In the script, the first example provided is an indefinite integral of a function involving x cubed and the square root of a quadratic expression. The concept is fundamental to the video's theme of integral computation.
💡Definite Integral
A definite integral is used to calculate the signed area under a curve between two points on the x-axis. The second example in the script is a definite integral with limits from 1 to e, involving x squared and a logarithmic function. The explanation of how to approach this type of integral is a key part of the video's educational content.
💡Substitution
Substitution is a common technique in calculus for simplifying integrals. The script suggests using substitution by setting u equal to a part of the integrand, which can make the integral easier to solve. This method is exemplified in the first integral problem where x squared plus 2 is substituted with u.
💡Integration by Parts
Integration by parts is a specialized technique for integrating products of functions, typically used when the integral is a product of a polynomial and a logarithmic function. The script discusses this method as a potential approach for both integrals, and it is applied in detail to the second integral problem involving x squared and ln(x squared).
💡Trigonometric Substitution
Trigonometric substitution is a method used to simplify integrals involving square roots, often by relating the integrand to trigonometric identities. The script briefly mentions this as a potential method for the first integral but concludes that a regular substitution is simpler in this case.
💡Square Root
The square root function is fundamental in mathematics and appears in the first integral of the script as part of the expression x squared plus 2 under a square root. The video discusses how to handle such expressions through substitution to simplify the integral.
💡Polynomial
A polynomial is an expression consisting of variables and coefficients involving only the operations of addition, subtraction, and multiplication. The script refers to polynomials as terms that are easier to differentiate than to integrate, which is a key insight when choosing what to integrate by parts.
💡Logarithm
The logarithm is a mathematical function that is the inverse of exponentiation. In the script, the logarithm appears in the second integral as ln(x squared), and the video discusses the preference for differentiating logarithms rather than integrating them when using integration by parts.
💡Chain Rule
The chain rule is a fundamental calculus rule for differentiating composite functions. The script mentions the chain rule when differentiating ln(x squared) to find u prime, which is necessary for setting up the integration by parts for the second integral.
💡Antiderivative
An antiderivative is a function whose derivative is the original function of the integral. The script discusses finding antiderivatives as part of the process of solving integrals, particularly after a successful substitution or integration by parts.
Highlights

Introduction to solving two integrals using different techniques.

First integral involves x^3 * sqrt(x^2 + 2) dx, suggesting trig substitution, integration by parts, or regular substitution.

Second integral is a definite integral from 1 to e of x^2 * ln(x^2) dx, with potential for regular substitution or integration by parts.

Choosing regular substitution for the first integral as the simplest method to try first.

Setting u = x^2 + 2 for substitution simplifies the integral significantly.

Substitution results in an integral of powers of u, making the problem straightforward to solve.

Final answer for the first integral involves back substitution to replace u with x and simplification.

For the second integral, considering the form of the integrand suggests trying integration by parts directly.

Deciding on u = ln(x^2) and v' = x^2 for integration by parts to simplify the integrand.

Integration by parts formula is applied, resulting in a simpler expression involving x^3/3 * ln(x^2).

The definite integral requires evaluating the simplified expression at the bounds 1 and e.

Further simplification leads to an integral involving x^2 * ln(x), which is a simpler form than the original integrand.

Recognizing that the simplified form is still amenable to further integration by parts.

Applying integration by parts again to the simplified integral, focusing on the ln(x) term.

Final steps involve evaluating constants and integrating a polynomial, which is a standard process.

The final answer for the second integral is given as 5e^3/27 - 2/27 after completing all steps.

Emphasis on the importance of choosing the right technique and simplifying the problem step by step.

Transcripts

Browse More Related Video

Calculus 2 Final Exam Review -

_-substitution: definite integrals | AP Calculus AB | Khan Academy

Lesson 16- Integration By Trig Substitution (Calculus 1 Tutor)

Indefinite Integral

Integration Practice IV | MIT 18.01SC Single Variable Calculus, Fall 2010

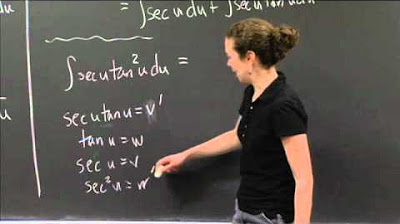
Integration Practice II | MIT 18.01SC Single Variable Calculus, Fall 2010

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Integral TechniquesCalculus ProblemsTrig SubstitutionsIntegration by PartsRegular SubstitutionPolynomial IntegrationLogarithmic FunctionsDefinite IntegralsEducational ContentMathematical Analysis