AP Calculus AB Crash Course Day 6 - Limits, Continuity, and the Intermediate Value Theorem
TLDRThe video script delves into various mathematical concepts and problems, starting with the limit of sine cubed over x cubed as x approaches zero, which is simplified by recognizing a common factor and using substitution. It then explores the limit of a logarithmic function and demonstrates two methods to solve it: recognizing it as a derivative and applying L'Hôpital's rule. The script also discusses the continuity of a piecewise-defined function and the conditions for a function to be continuous at a certain point. Furthermore, it examines the concavity of a differentiable function by analyzing its first and second derivatives. The video concludes with the application of the intermediate value theorem to a composite function, illustrating the theorem's utility in finding a value that satisfies a given condition within a continuous function's range.
Takeaways
- 📖 The limit of (sin(x)/x) as x approaches 0 is 1, which is a common limit used in calculus and can be determined using L'Hôpital's rule.
- 🤦 When dealing with limits involving different powers of x, it can be helpful to introduce a new variable, such as u = 5x, to simplify the expression.
- 🔍 L'Hôpital's rule is a useful method for finding indeterminate limits of the form 0/0 or ∞/∞ by taking the derivatives of the numerator and denominator.
- 📉 The continuity of a function at a point can be determined by checking if the left and right limits at that point are equal to the function's value at that point.
- 📈 The first derivative of a function indicates where the function is increasing or decreasing, while the second derivative indicates concavity (whether the graph is concave up or down).
- 🌐 The intermediate value theorem states that a continuous function will take on any value between its given values over an interval, which is useful for finding specific function values.
- 🚫 If the left and right limits of a function at a point do not agree, the function is not continuous at that point.
- 🔢 The composition of two differentiable functions is also differentiable, and if both are continuous, their composition is continuous as well.
- 🔑 The existence of a relative maximum or minimum can be found where the first derivative of a function is zero and changes sign.
- 📶 The second derivative can be used to determine intervals of concavity for a function; if it's positive, the function is concave up, and if it's negative, the function is concave down.
- ⛓ When solving differential equations, the second derivative can provide information about the concavity of the solution curves in the x-y plane.
Q & A
What is the limit of sine cubed of 5x over x cubed as x approaches zero?
-The limit is 125. The script explains that by substituting u = 5x and using the known limit of sine x over x as x approaches zero, which is 1, the expression simplifies to 125 times 1 cubed.
How can we find the derivative of the natural logarithm function at a specific point?
-The derivative of ln x is found by using the definition of the derivative and applying the limit process. At a specific point, such as x = 10, the derivative is 1 over the value of x, which is 1/10 in this case.
What is the condition for the function f(x) = tan x / x to be continuous at x = 0?
-The function f(x) is continuous at x = 0 if the limit as x approaches 0 of f(x) is equal to f(0). However, the script shows that the limit as x approaches 0 is 1, while f(0) is 0, so the function is not continuous at x = 0.
Is the rate of water leakage from the tank, modeled by r(t), continuous at t = 4?
-No, the rate of water leakage is not continuous at t = 4. The left-hand limit and the right-hand limit as t approaches 4 do not agree, indicating a discontinuity at that point.
What does the second derivative of a function indicate?
-The second derivative of a function indicates the concavity of the function. If the second derivative is positive, the function is concave up, and if it is negative, the function is concave down.
How does the given differential equation dy/dx = y + 1/x describe the concavity of its solution curves?
-The solution curves of the given differential equation are always concave down since the second derivative, obtained by differentiating dy/dx with respect to x, is zero.
What is the Intermediate Value Theorem, and how does it apply to the function f(x) = h(k(x))?
-The Intermediate Value Theorem states that if a function is continuous on a closed interval and takes on values f(j) and f(k) at the endpoints of the interval, then for any value b between f(j) and f(k), there exists a value a in the interval such that f(a) = b. In the script, it is shown that for a value b between f(-3) and f(2), there exists an a such that f(a) = b.
What is the relationship between differentiability and continuity?
-Differentiability implies continuity. If a function is differentiable at a point, it is also continuous at that point. This is because the derivative of a function at a point requires the function to be continuous at that point.
How can we determine the x-coordinates of all relative minima and maxima of a differentiable function g?
-To determine the x-coordinates of all relative minima and maxima of a differentiable function g, one can find where the first derivative g'(x) is equal to zero and then analyze the sign of the first derivative around these points. A change from positive to negative indicates a local maximum, while a change from negative to positive indicates a local minimum.
What is the significance of the second derivative being zero in the context of the differential equation dy/dx = y + 1/x?
-A second derivative that is consistently zero, as in the case of the given differential equation, implies that there is no region where the solution curves are concave down or concave up. The solution curves maintain a constant concavity throughout the plane.
How does the script use the limit concept to simplify the expression for the function f(x) = h(k(x))?
-The script uses the limit concept to evaluate the function f(x) = h(k(x)) at specific points where x is -3 and 2, and then applies the Intermediate Value Theorem to assert the existence of a value a such that f(a) = b for b between f(-3) and f(2).
Outlines
🧮 Limit Calculations and Derivatives
The first paragraph discusses the calculation of limits and derivatives. It begins with a limit involving sine cubed and a polynomial, where the limit as x approaches zero of sine(x) over x is used, equal to one. This limit is a common one to remember and can be derived using L'Hôpital's rule if forgotten. The paragraph then covers a limit involving a natural logarithm function, which is approached by recognizing it as a derivative and applying the definition of a derivative. Two methods are shown: using the derivative shortcut and L'Hôpital's rule. Lastly, the continuity of a piecewise function at x equals zero is discussed, with the conclusion that the function is not continuous at that point.
📐 Continuity and Differentiability
The second paragraph explores the concepts of continuity and differentiability. It starts with a piecewise function defined by f(x) and examines the limit as x approaches zero, showing that it exists and is equal to one. The continuity of the function at x equals zero is then discussed, revealing that the function is not continuous at that point. The paragraph moves on to discuss the continuity of a function r(t) that models the rate at which water leaks from a tank, concluding that the function is not continuous at t equals 4. Finally, the paragraph addresses finding the x-coordinates of relative minima and maxima for a differentiable function g, and determining the intervals where the graph of g is concave up or down.
📉 Concavity and Differential Equations
The third paragraph delves into concavity and differential equations. It begins by examining the second derivative of a function to determine concavity, identifying where the second derivative is zero, positive, or negative to find intervals of concavity. The paragraph then considers a differential equation and describes the region in the xy-plane where all solution curves to the differential equation are concave down, concluding that there are no such curves since the second derivative is always zero. Lastly, the paragraph discusses the composition of twice differentiable functions h and k, and uses the intermediate value theorem to show that there must be a value a such that f(a) equals a given value b, for a between negative 3 and 2, exclusive.
🔍 Intermediate Value Theorem Application
The fourth paragraph focuses on the application of the intermediate value theorem. It starts by establishing that the function f, composed of h and k, is continuous because it is the composition of two continuous functions. The values of f at specific points are given, and it is shown that b lies between these values. The intermediate value theorem is then used to assert that for any value b between f(-3) and f(2), there exists an a such that f(a) equals b. A visual representation is suggested to better understand the theorem's application, emphasizing the lack of breaks in the curve of a continuous function.
Mindmap
Keywords
💡Limit
💡L'Hôpital's Rule
💡Derivative
💡Piecewise Function
💡Continuity
💡Concavity
💡Differential Equation
💡Chain Rule
💡Quotient Rule
💡Intermediate Value Theorem
💡Natural Logarithm
Highlights
The limit as x approaches zero of sine cubed x over x cubed is calculated using the fact that the limit of sine x over x is equal to one.
L'Hôpital's rule can be used to find the limit of sine x over x, but it's a common limit to remember for frequent use.
A substitution method is introduced to simplify the expression by letting u equal 5x, which helps in evaluating the limit.
The limit as h approaches zero of one over h times the natural logarithm of (10 plus h) over 10 can be solved using the derivative shortcut or L'Hôpital's rule.
The derivative of the natural logarithm function at 10 is found to be 1/10, which matches the limit calculation.
The function f(x) is defined piecewise, with tan x over x for x not equal to zero and zero for x equal to zero.
The limit as x approaches zero of f(x) exists and is equal to one, using L'Hôpital's rule.
The function f is continuous at x equals zero since f(0) is defined and equals zero.
The water leakage rate from a 5,000-gallon tank is modeled by a piecewise function, with different rates for t between 0 and 4 and t greater than 4.
The continuity of the leakage rate function r(t) at t equals 4 is determined by calculating left and right-hand limits.
The function g(x) is differentiable with a domain of all positive real numbers, and its derivative is given by a specific formula.
The x-coordinates of all relative minima and maxima of g(x) are found by analyzing the first derivative.
The concavity of g(x) is determined by examining the second derivative, which reveals intervals where the graph is concave up or down.
A differential equation dy/dx = y + 1/x is analyzed to describe regions in the xy-plane where solution curves are concave down.
The second derivative of the given differential equation is calculated to be zero, indicating no concavity in the solution curves.
Functions h(x) and k(x) are twice differentiable with specific values at given points, and the composition f(x) = h(k(x)) is continuous.
The Intermediate Value Theorem is applied to show that there exists a value 'a' such that f(a) equals a given value 'b', within a specified range.
Transcripts
Browse More Related Video

AP Calculus AB Crash Course Day 3 - Limits, Continuity, and Differentiation
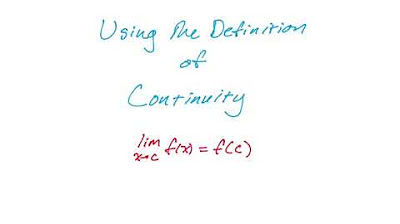
Using the Definition of Continuity in Calculus

2021 AP Calculus AB Free Response #4 (First Administration)

Is the function continuous?

1.2 - Algebraic Limits and Continuity

AP Calculus AB Crash Course Day 10 - Integration, IVT, and MVT
5.0 / 5 (0 votes)
Thanks for rating: