Euler's Method (introduction & example)
TLDRThe video script introduces the audience to the numerical approach known as Euler's method for solving differential equations. It begins with a basic explanation of the method, emphasizing its application when an explicit function Y as a function of X is difficult to obtain. The script outlines the process of using the given first derivative dy/dx to approximate the solution by taking incremental steps, calculating the slope at each point, and then advancing to the next point using the point-slope form of a line. The importance of step size H is highlighted, noting that smaller steps lead to better approximations. The script also demonstrates the method using an example where dy/dx = 3x + y with the initial condition y(0) = -1, and aims to approximate y(0.2) with a step size of 0.04. The process is detailed, showing each step's calculation and emphasizing the need for patience and organization. Finally, the script compares the numerical approximation with the exact solution of the differential equation, showcasing the effectiveness of Euler's method.
Takeaways
- 📚 The video introduces the numerical approach to solving differential equations, specifically focusing on the oldest method.
- 🔍 Given a first derivative dy/dx, the method involves finding an expression in terms of x and y, even when it's difficult to solve analytically.
- 📈 The concept is based on using an initial point (x₀, y₀) and approximating the solution by taking incremental steps, with the step size denoted as H.
- 🧮 The slope of the tangent line at a given point is calculated using the derivative dy/dx, which guides the direction and magnitude of each step.
- 📐 The point-slope form of a line is used to find the equation of the line that passes through the current point and has the calculated slope.
- 🔢 The slope value (M) is obtained by plugging the current x and y values into the derivative expression, which is represented as f(x, y).
- 🚶♂️ The process involves moving from one point to the next by taking a step in the direction indicated by the slope, with the distance of the step being the step size H.
- 🔄 This iterative process is repeated, using the newly calculated slope at each step to find the next point, until the desired x value is reached.
- 📈 Euler's method is highlighted as a way to approximate the solution to a differential equation, especially when an exact solution is not feasible.
- 📉 An example is provided to demonstrate the method, using the differential equation dy/dx = 3x + y with the initial condition y(0) = -1, and approximating y at x = 0.2 with a step size of 0.04.
- 🤔 The importance of patience and organization is emphasized for successfully applying the method, especially when dealing with complex calculations or programming.
- 📝 The video also mentions that for certain types of differential equations, such as those that are not separable, different techniques like the integrating factor may be necessary, which is covered in other videos.
Q & A
What is the numerical approach discussed in the video?
-The numerical approach discussed in the video is the Euler's method, which is used to approximate solutions to differential equations.
What is the significance of the first derivative dy/dx in the context of the video?
-The first derivative dy/dx represents the slope of the tangent line at a given point (x, y), which is crucial for determining the direction and magnitude of the next step in the Euler's method.
How does the slope of the tangent line help in approximating the solution to a differential equation?
-The slope of the tangent line indicates the direction and steepness of the curve at a specific point. By using this slope, one can estimate the next point on the curve by taking a step in the direction of the slope over a certain distance, known as the step size.
What is the formula for the point-slope form of a line used in the Euler's method?
-The point-slope form of a line used in the Euler's method is given by y1 - y0 = m(x1 - x0), where m is the slope of the line at the point (x0, y0).
How is the step size (H) determined in the Euler's method?
-The step size (H) in the Euler's method is a predetermined value that dictates how far one should move along the x-axis to estimate the next point on the curve. A smaller step size generally leads to a more accurate approximation.
What is the formula used to calculate the next point (x1, y1) in the Euler's method?
-The formula to calculate the next point (x1, y1) in the Euler's method is y1 = y0 + H * f(x0, y0), where f(x0, y0) is the slope function evaluated at the initial point (x0, y0), and H is the step size.
What is the role of the initial condition in the Euler's method?
-The initial condition provides the starting point (x0, y0) for the Euler's method. It is essential for beginning the iterative process of approximating the solution to the differential equation.
How does the Euler's method handle differential equations that are not separable?
-The Euler's method can still be applied to non-separable differential equations by using the given derivative and initial conditions to approximate the solution iteratively, without the need for separation or integration of the equation.
What is the advantage of using a smaller step size in the Euler's method?
-Using a smaller step size in the Euler's method generally results in a more accurate approximation of the solution to the differential equation, as it reduces the error introduced in each step.
How does the Euler's method relate to the concept of a slope field?
-The Euler's method utilizes the concept of a slope field by using the derivative of the function to determine the slope of the tangent line at each point, which guides the iterative process of approximating the solution to the differential equation.
What is an example of a differential equation and initial condition used in the video?
-An example given in the video is the differential equation dy/dx = 3x + y with the initial condition y(0) = -1. The goal is to approximate the value of y at x = 0.2 using the Euler's method with a step size of 0.04.
How does the accuracy of the Euler's method compare to the actual solution of the differential equation?
-The accuracy of the Euler's method is an approximation and depends on the step size used. If the step size is small enough, the polygonal line formed by the method can be very close to the actual curve of the solution. However, it will not be exact unless the step size approaches zero.
Outlines
📐 Introduction to Numerical Methods for Solving Differential Equations
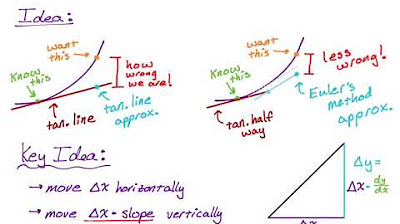
This paragraph introduces the numerical approach to solving differential equations. The idea is that if we are given the first derivative dy/dx in terms of x and y, and an initial point (x, y), we can approximate the solution by taking small steps from the initial point and calculating the slope at each point. The slope tells us the direction to move and the step size determines how far to go. The process is iterative, with each step using the slope at the previous point to determine the next point. This is similar to the concept of a slope field. The paragraph also introduces the point-slope form of a line and the Euler's method for numerically approximating solutions to differential equations.
🔢 Euler's Method: Step by Step Calculation
This paragraph provides a detailed step-by-step explanation of how to apply Euler's method to approximate the solution to a differential equation. The process involves iterating through the following steps: 1. Calculate the slope (M) at the current point using the differential equation. 2. Use the point-slope form of a line to find the equation of the tangent line at the current point. 3. Determine the next point by taking a step of size H in the direction of the slope. 4. Repeat the process, using the newly calculated point as the starting point for the next iteration. The paragraph also provides an example using the differential equation dy/dx = 3x + y with initial condition y(0) = -1, and shows how to approximate y(0.2) using a step size of 0.04. The calculations are demonstrated in detail, emphasizing the need for patience and organization.
📈 Approximation vs. Exact Solution
This paragraph discusses the relationship between the approximation obtained using Euler's method and the exact solution to the differential equation. It is shown that if the step size H is kept small, the polygonal line formed by the approximation will closely follow the actual curve y = f(x). The exact solution to the given differential equation is provided as y(x) = 2e^x - 3x - 3. By plugging in x = 0.2, the exact value of y(0.2) is calculated and compared to the approximation obtained using Euler's method. The approximation is found to be quite close to the exact value, demonstrating the effectiveness of the numerical method.
Mindmap
Keywords
💡Differential Equations
💡Numerical Approach
💡Derivative
💡Tangent Line
💡Slope Field
💡Approximation
💡Euler's Method
💡Step Size
💡Initial Condition
💡Point-Slope Form
💡Integration Factor
Highlights
Introduction to the numerical approach for solving differential equations using the Euler's method
Given the first derivative dy/dx as an expression in terms of x and y
Starting with an initial point (x0, y0) and approximating the solution iteratively
Calculating the slope of the tangent line at the given point using the derivative
Using the slope to determine the direction and distance to move to the next point
Smaller step sizes result in better approximations
Deriving the point-slope form of the line equation based on two points
Expressing the slope as a function f(x, y) using the given differential equation
Introducing the step size H and its role in determining the distance between points
Applying the Euler's method iteratively to approximate y at successive x values
Using the previous y value and the slope at that point to calculate the next y value
Visualizing the approximation as a polygonal line that closely resembles the actual curve
Demonstrating the Euler's method with a specific example problem
Given differential equation dy/dx = 3x + y and initial condition y(0) = -1
Approximating y at x = 0.2 using a step size of 0.04
Iterative process of calculating y values at each step using the slope and step size
Final approximation of y at x = 0.2 is -1.1667
Comparing the numerical approximation with the exact solution y = 2e^x - 3x - 3
The Euler's method provides a good approximation when the step size is small enough
Transcripts
Browse More Related Video

Euler's Method - Example 1

Calculus BC – 7.5 Approximating Solutions Using Euler’s Method

Euler's Method Differential Equations, Examples, Numerical Methods, Calculus
Euler's Method for Approximating Values of a Function

AP Calculus BC Lesson 7.5

Euler's method | Differential equations| AP Calculus BC | Khan Academy
5.0 / 5 (0 votes)
Thanks for rating: