Finding a P-value given the test statistic

AspireMtnAcademy
10 Nov 201803:40
EducationalLearning
32 Likes 10 Comments

TLDRIn this informative video, Professor Curtis from Aspire Mountain Academy guides viewers through the process of finding a p-value for a hypothesis test. The scenario involves a claim about the mean data speed of smartphone carriers at airports, with a given sample size and test statistic. Curtis explains that the p-value represents the area in the tail of the distribution, which is bounded by the test statistic. He demonstrates the use of the Student T-distribution, given the T-score nature of the test statistic, and calculates the degrees of freedom. The video then explores setting up the correct inequality for the alternative hypothesis, accounting for a two-tailed test. Using StatCrunch, Curtis shows how to input the positive and negative T-statistics and compute the p-value by taking the complement of the area between the tails. The video concludes with an invitation for viewers to engage with the academy for more statistics help and feedback.

Takeaways
  • 📚 The p-value is the area in the tail of the distribution bounded by the test statistic, which provides the boundary for that area.
  • 📊 The test statistic given in the problem is a t-score, indicating that the Student's t-distribution should be used for the hypothesis test.
  • 🔢 Degrees of freedom for the t-distribution are calculated as one less than the sample size, which in this case is 28 (n=29).
  • ⚖️ The null hypothesis claims that the mean data speed is 18.00 megabytes per second, with equality belonging to the null hypothesis.
  • 🔁 The alternative hypothesis is the complement of the null hypothesis, resulting in a two-tailed test since the claim is about not being equal to 18.00.
  • 💡 In StatCrunch, the 'between' option is used for a two-tailed test, as it splits the p-value between the left and right tail of the distribution.
  • 📐 The test statistic values (positive and negative) are input into the Student t-calculator in StatCrunch to find the p-value.
  • 🧮 The p-value is found by taking the complement of the area between the tails calculated by StatCrunch, as the p-value represents the area of the tails.
  • 📈 The final p-value is rounded to three decimal places for accuracy.
  • 📝 It's important to understand the concept of p-value and how it is derived from the test statistic and the chosen distribution.
  • 🌟 Aspire Mountain Academy offers more statistics help and lecture videos for those needing additional assistance in learning statistics.
  • ✅ Engage with the community by leaving comments and providing feedback on the content for continuous improvement.
Q & A

  • What is the main topic of the video?

    -The main topic of the video is how to find a p-value given a test statistic within the context of a hypothesis test related to data speeds of smartphone carriers at airports.

  • What is the claim being tested in the hypothesis?

    -The claim being tested is that the mean data speed for smartphone carriers at airports is 18.00 megabytes per second.

  • What is the sample size used in the hypothesis test?

    -The sample size used in the hypothesis test is 29.

  • What is the test statistic value given in the problem statement?

    -The test statistic value given is T equals 2.074.

  • Why is the test statistic important in finding the p-value?

    -The test statistic is important because it provides the boundary for the area in the distribution that the p-value represents.

  • Which distribution is being used for the hypothesis test?

    -The Student T-distribution is being used for the hypothesis test because the test statistic is a T-score.

  • How is the degrees of freedom calculated for the Student T-distribution?

    -The degrees of freedom is calculated as one less than the sample size, which in this case is 28 (29 - 1).

  • What does the alternative hypothesis represent in this context?

    -The alternative hypothesis represents the complement of the null hypothesis, indicating that the mean is not equal to 18.00 megabytes per second, which leads to a two-tailed test.

  • How does one determine the p-value using StatCrunch?

    -One determines the p-value by using the Student T-distribution calculator in StatCrunch, inputting the test statistic and degrees of freedom, and then taking the complement of the area between the tails.

  • What is the significance of a two-tailed test in this scenario?

    -A two-tailed test is significant because it considers both directions from the mean (both higher and lower values), which is appropriate when the alternative hypothesis is that the mean is not equal to a certain value.

  • What is the final step to find the p-value using the calculator?

    -The final step is to compute the area between the tails using the calculator, and then take the complement of this area to find the p-value in the tails.

  • How does the video conclude?

    -The video concludes by encouraging viewers to leave comments, visit Aspire Mountain Academy for more statistics help, and offering to provide additional lecture videos or feedback.

Outlines
00:00
📚 Understanding P-Values in Hypothesis Testing

Professor Curtis introduces the concept of p-values in the context of hypothesis testing. He explains that a p-value is the area in the tail of a distribution that is bounded by the test statistic. The problem statement involves determining the p-value for a claim about the mean data speed of smartphone carriers at airports, with a given sample size and test statistic. The test statistic is a t-score, indicating the use of the Student's t-distribution. The professor uses StatCrunch to calculate the p-value, considering the degrees of freedom and the alternative hypothesis, which is a two-tailed test due to the complement of the equality in the claim. The final step involves computing the p-value as the complement of the area between the tails of the distribution.

Mindmap
Keywords
💡p-value
The p-value is a statistical measure that indicates the strength of the evidence against the null hypothesis. In the context of the video, it is the area in the tail of the distribution that is bounded by the test statistic. It is crucial for hypothesis testing as it helps determine whether the observed data is statistically significant. The video demonstrates how to find the p-value using a t-score from a Student T distribution.
💡test statistic
A test statistic is a summary value calculated from sample data during a statistical test. It is used to determine the p-value and make decisions about the null hypothesis. In the video, the test statistic is a t-score of 2.074, which provides the boundary for the area under the distribution curve that will be used to calculate the p-value.
💡Student T distribution
The Student T distribution, also known as the t-distribution, is a type of probability distribution that is used in statistical hypothesis testing when the sample size is small and the population standard deviation is unknown. The video discusses using the Student T distribution to find the p-value for the given hypothesis test, as indicated by the t-score test statistic.
💡degrees of freedom
Degrees of freedom in statistics refer to the number of values in the data set that are free to vary independently. It is a key concept in hypothesis testing and is used to determine the appropriate distribution for the test statistic. In the script, the degrees of freedom are calculated as one less than the sample size, which is 28 in this case, and is used to select the correct Student T distribution.
💡null hypothesis
The null hypothesis is a statement of no effect or no difference that researchers test statistically. It usually represents a default position that there is no relationship between the variables being studied. In the video, the null hypothesis is that the mean data speed of smartphone carriers at airports is 18.00 megabytes per second.
💡alternative hypothesis
The alternative hypothesis is a statement that contradicts the null hypothesis and represents what the researcher believes to be true. It is used to frame the research question and determine the direction of the test. In the video, the alternative hypothesis is that the mean data speed is not equal to 18.00 megabytes per second, leading to a two-tailed test.
💡two-tailed test
A two-tailed test is a type of statistical test in which the critical area for rejecting the null hypothesis is divided between the two tails of the distribution. It is used when the alternative hypothesis predicts that the test statistic could be either greater than or less than the value specified in the null hypothesis. The video explains that since the claim of equal mean is the null hypothesis, the alternative is that it is not equal, thus requiring a two-tailed test.
💡sample size
Sample size refers to the number of observations or elements in a sample used for a particular analysis. It is an important factor in determining the power of a statistical test and the degrees of freedom. In the video, the sample size is given as 29, which is used to calculate the degrees of freedom and is a key piece of information for the hypothesis test.
💡statistical significance
Statistical significance is a measure that determines whether the results of a statistical test are likely to have occurred by chance. It is often assessed using the p-value, where a lower p-value indicates stronger evidence against the null hypothesis. The video demonstrates how to find the p-value to assess the statistical significance of the data speeds at airports.
💡complement
In statistics, the complement of a probability refers to the probability that the event does not occur. In the context of the video, the complement is used to find the p-value by subtracting the area between the tails from 1, since the p-value represents the area in the tails of the distribution. The complement is calculated as 1 minus the area between the tails as shown in the video.
💡StatCrunch
StatCrunch is a web-based statistical software that allows users to perform a variety of statistical tests and calculations. In the video, StatCrunch is used to calculate the p-value by inputting the test statistic, degrees of freedom, and selecting the appropriate distribution. It is a tool that helps in visualizing and computing statistical measures, making it easier to understand and apply statistical concepts.
Highlights

Professor Curtis from Aspire Mountain Academy is providing statistics homework help.

The focus is on learning how to find a p-value given a test statistic.

The problem statement involves a hypothesis test about smartphone carriers' data speeds at airports.

The claim is that the mean data speed is 18.00 megabytes per second.

The sample size for the test is 29.

The test statistic (T-score) given is 2.074.

The p-value is the area in the tail of the distribution bounded by the test statistic.

The test statistic is a T-score, indicating the use of the Student T-distribution.

StatCrunch is used to calculate the p-value using the Student T-distribution.

Degrees of freedom are calculated as one less than the sample size, resulting in 28.

The alternative hypothesis is determined by the complement of the null hypothesis, leading to a two-tailed test.

The p-value is split between the left and right tail of the distribution.

Positive and negative T-statistics are entered into the calculator for the two-tailed test.

The final p-value is obtained by taking the complement of the area between the tails.

The p-value is rounded to three decimal places.

Aspire Mountain Academy encourages feedback and comments to improve their statistics help.

Students can access more lecture videos or provide feedback on what they'd like to see next.

The video concludes with an invitation to see the next video in the series.

Transcripts

Browse More Related Video

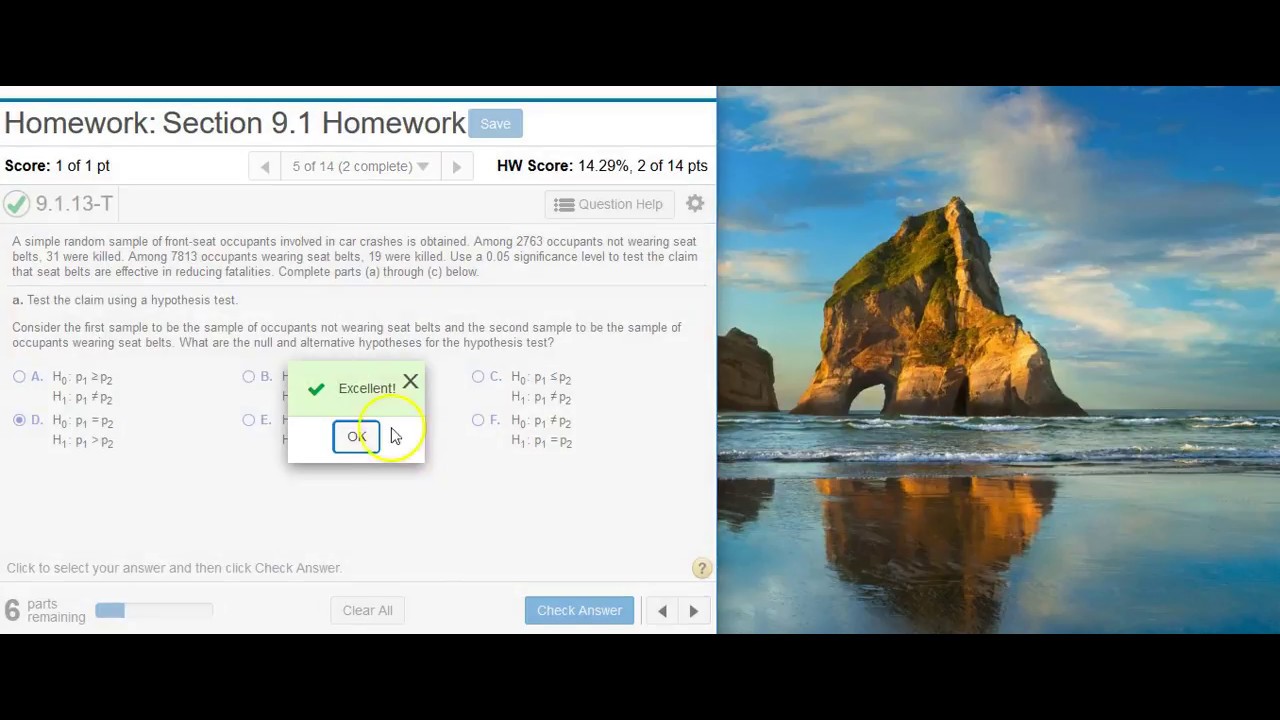
Performing hypothesis testing on two proportions in StatCrunch

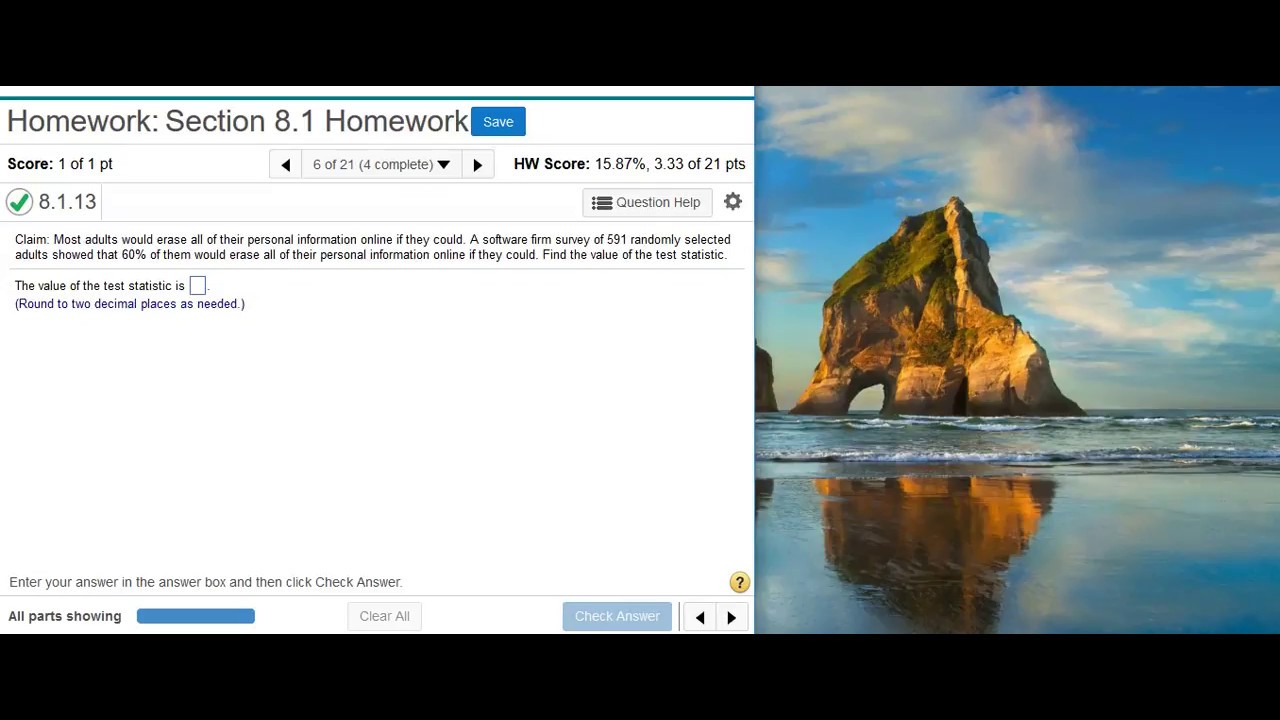
Finding the value of the test statistic for hypothesis testing on proportions

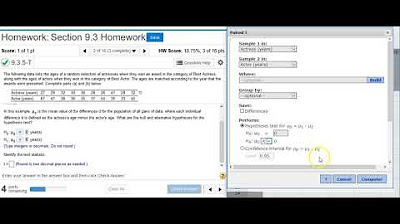
Using StatCrunch to perform hypothesis testing on two matched pair means of acting award ages

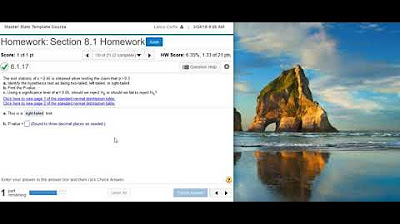
Using a z-score to complete hypothesis testing for a claim of equality

Using StatCrunch to perform hypothesis testing on two proportions of referee calls

Calculating a p-value for a Two-tailed Test

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
StatisticsHypothesis TestingP-ValueStudent T-DistributionData SpeedAirportsSample SizeTest StatisticEducational VideoAspire Mountain AcademyLearn Stats