AP Physics Workbook 7.A Relationship between Arc Length and Angle of Rotation
TLDRThe video script discusses the relationship between arc length and angle in radians, using data collected from a coin on a rotating turntable. It explains how to calculate the angle in radians using the formula angle equals arc length divided by radius, and emphasizes the linear relationship between arc length and angle. The video further illustrates how to graph this relationship and calculate the slope, which is found to be equal to the radius. This concept is then related to the linear equation y=MX+B, where the output (arc length) is the product of the slope (radius) and the input (angle in radians).
Takeaways
- 📚 The relationship between arc length and angle is explored in the context of a rotating turntable and a coin resting on it.
- 📐 Radian measure is introduced as the unit for angles, defined by an arc whose length is equal to its radius.
- 🔢 The formula for calculating angle in radians is given by angle (in radians) = arc length / radius.
- 🌐 The video script provides a step-by-step process for calculating the angle in radians using given arc lengths and radii.
- 📈 A graph is suggested to be created to visually represent the relationship between arc length and angle in radians, using trials one through five where the radius is constant.
- 🛠️ Excel is mentioned as a tool for creating the graph, with specific instructions on inputting values and generating a scatter plot.
- 📶 The significance of the slope in the context of the arc length versus angle graph is that it represents the radius.
- 🔍 The linear relationship between arc length and angle in radians is emphasized, highlighting the direct proportionality.
- 💡 The concept of slope is linked to physical quantities, where the slope (radius) multiplied by the angle in radians gives the arc length (output).
- 📌 A comparison is made between the linear equations in physics and those in mathematics, showing the similarity in how they describe relationships.
- 🎯 The final arc length can be thought of as the final position in a circular path, with the radius analogous to velocity and the angle to time.
Q & A
What is the relationship between arc length and angle discussed in the transcript?
-The relationship between arc length and angle is that the angle is equal to the arc length divided by the radius. This relationship is fundamental in understanding how angles and arc lengths interact in the context of circular motion.
How is one Radian defined in the context of the transcript?
-One Radian is defined as the angle subtended by an arc whose length is equal to the radius. This definition is crucial for converting between arc lengths and angles in radians.
What is the significance of using trials one through five for graphing arc length versus angle in radians?
-Trials one through five are significant for graphing because in these trials, the radius remains constant. This allows the arc length to be solely a function of the angle in radians, making it possible to create a meaningful and accurate graph.
Why can't trials after six be used for the graph in the context of the transcript?
-Trials after six cannot be used for the graph because the radius changes in these trials. A changing radius means that the arc length is no longer solely a function of the angle in radians, which would invalidate the graph's accuracy and consistency.
How does the process of calculating the slope of the line of best fit involve the data points?
-The slope of the line of best fit is calculated using the formula for slope, which is the change in y (Delta Y) over the change in x (Delta X). This involves taking two data points, subtracting their y-values (the arc lengths) to find Delta Y, and subtracting their x-values (the angles in radians) to find Delta X. The slope is then found by dividing Delta Y by Delta X.
What does the slope of the line of best fit represent in the context of the arc length versus angle in radians graph?
-In the context of the arc length versus angle in radians graph, the slope of the line of best fit represents the radius. This is because the relationship between arc length and angle in radians is linear, and the slope reflects this relationship directly.
How can the linear equation y = mx + b be applied to the context of arc length and radius?
-The linear equation y = mx + b, where y is the output (arc length), m is the slope (radius), x is the input (angle in radians), and b is the starting value, can be applied to the context of arc length and radius by recognizing that the arc length is the output when the input (angle in radians) is multiplied by the slope (radius). In this case, b (the starting value) is assumed to be zero since we consider the starting arc length to be zero.
What is the significance of the starting arc length in the context of the arc length versus angle in radians?
-In the context of the arc length versus angle in radians, the starting arc length is typically assumed to be zero. This assumption simplifies the linear relationship between the arc length (output) and the angle in radians (input), as it directly relates the arc length to the radius and the angle without the need to account for an initial starting position.
How does the concept of final position in linear equations relate to arc length in the context of circular motion?
-In linear equations, the final position is determined by the equation final position = velocity (or speed) × time + starting value. Similarly, in circular motion, the arc length (final position) is determined by the radius (analogous to velocity) multiplied by the angle in radians (analogous to time), with the starting arc length assumed to be zero.
What is the practical application of understanding the relationship between radius, angle, and arc length?
-Understanding the relationship between radius, angle, and arc length is crucial in various fields such as physics, engineering, and mathematics, especially when dealing with circular motion, mechanical systems, and geometrical problems. It allows for accurate calculations and predictions of motion, design of mechanical components, and solutions to geometric problems involving circles.
How can the concepts discussed in the transcript be applied to real-world scenarios involving circular motion?
-The concepts discussed in the transcript can be applied to real-world scenarios such as calculating the distance covered by a wheel rotating a certain number of radians, determining the angle through which a satellite must adjust its antenna to maintain communication with a ground station, or designing mechanisms like turntables and Ferris wheels where precise control of motion is required.
Outlines
📚 Introduction to Torque and Rotation Concepts
This paragraph introduces the topic of the video, which is focused on unit 7 of the AP Physics workbook, specifically dealing with torque and rotation. It sets the scene by mentioning a coin resting on a rotating turntable and the data collected by Angelica regarding the distance (radius) and the arc length the coin travels as it turns through various angles. The paragraph emphasizes the importance of understanding the relationship between arc length and angle, and introduces the concept of radians. It also provides an equation to calculate the angle in radians and demonstrates how to use it with given values. The paragraph concludes by encouraging viewers to take notes and understand the significance of the concepts discussed.
📈 Creating a Graph of Arc Length vs. Angle in Radians
In this paragraph, the focus shifts to the practical application of the concepts discussed earlier. The speaker explains how to create a graph that represents the relationship between arc length and angle in radians. It is suggested that only trials one through five should be used for the graph, as the radius remains constant in these trials, making the arc length solely dependent on the angle in radians. The paragraph provides a step-by-step guide on how to input the values into Excel and create a scatter plot, followed by instructions on how to add a trendline and display the equation. The aim is to visually represent the linear relationship between arc length and angle, and to ensure that the line of best fit has an equal number of data points above and below it.
📊 Calculating and Interpreting the Slope
This paragraph delves into the mathematical aspect of the relationship between arc length and angle. The speaker explains how to calculate the slope using two data points and the formula for slope (Delta Y over Delta X). The significance of the slope is highlighted by revealing that it is equal to the radius in this context. The paragraph emphasizes the linear relationship between arc length, angle in radians, and the radius. It also introduces the equation of a line (y = mx + b) and relates it to the physical quantities being discussed, where the output (y) is the arc length, the slope (m) is the radius, and the input (x) is the angle in radians. The paragraph concludes by drawing an analogy between this linear relationship and the concept of final velocity and position in physics.
🎓 Summary of Solutions for Section 7.8
The final paragraph serves as a brief conclusion to the video's content. It summarizes the solutions for section 7.8 of the AP Physics workbook, which includes the concepts and calculations related to torque, rotation, arc length, and angle in radians. The paragraph reiterates the importance of understanding these concepts and their interrelationships, and it provides a succinct wrap-up of the video's educational content.
Mindmap
Keywords
💡Arc Length
💡Radian
💡Rotation
💡Turntable
💡Graph
💡Slope
💡Linear Relationship
💡Excel
💡Trials
💡Line of Best Fit
💡Data Points
Highlights
Introduction to the relationship between arc length and angle in physics.
Explanation of how to feel in the angles in radiance through the given data.
Definition of one Radian as an angle subtended by an arc whose length is equal to the radius.
Presentation of the equation relating angle to arc length and radius.
Demonstration of how to calculate the radiant angle in radians using given arc lengths and radii.
Discussion on the importance of using trials one through five for graphing due to the constant radius.
Procedure for creating a graph of arc length versus angle in radians using Excel.
Explanation of how to sketch the line of best fit for the data on a graph.
Calculation of the slope using the data points from the graph.
Significance of the slope as it relates to the radius in the context of the experiment.
Derivation of the linear equation relating arc length, radius, and angle in radians.
Analogous relationship between arc length, radius, and angle compared to the linear equations of velocity, distance, and time.
Final summary of the solutions for unit 7, section 7.a.
Transcripts
Browse More Related Video
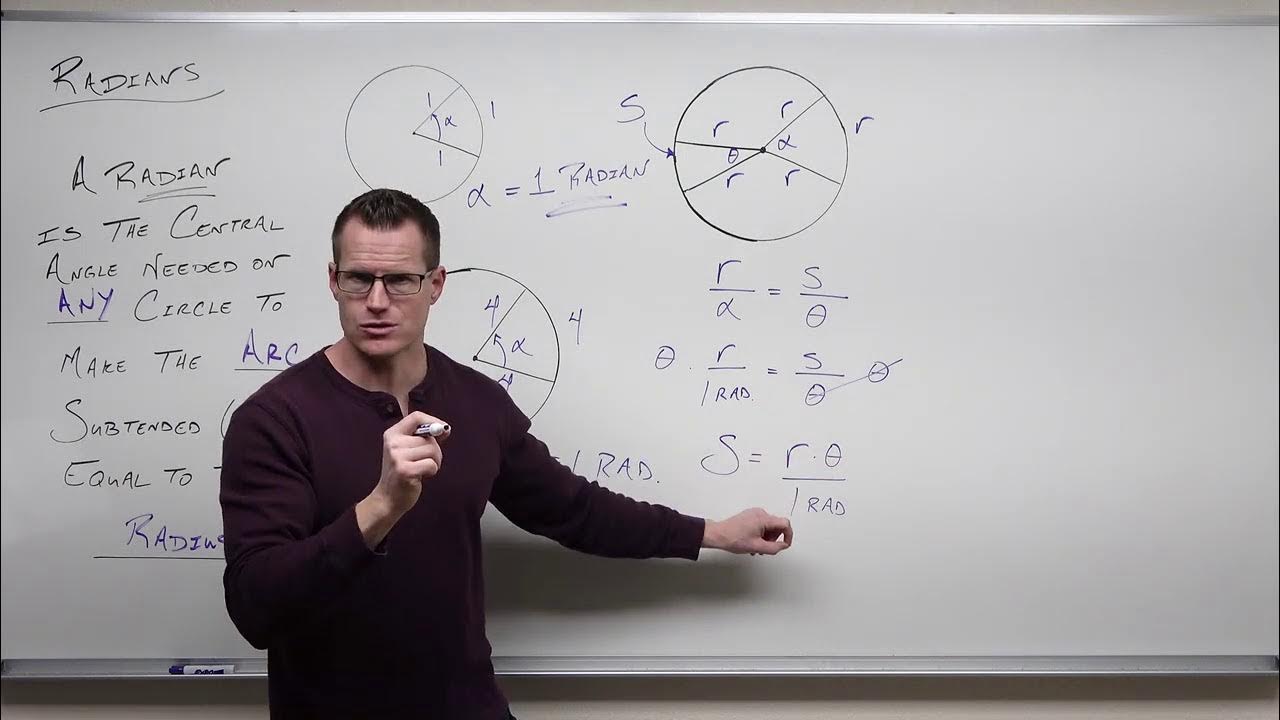
Introduction to Radians (Precalculus - Trigonometry 3)

Radians and Degrees
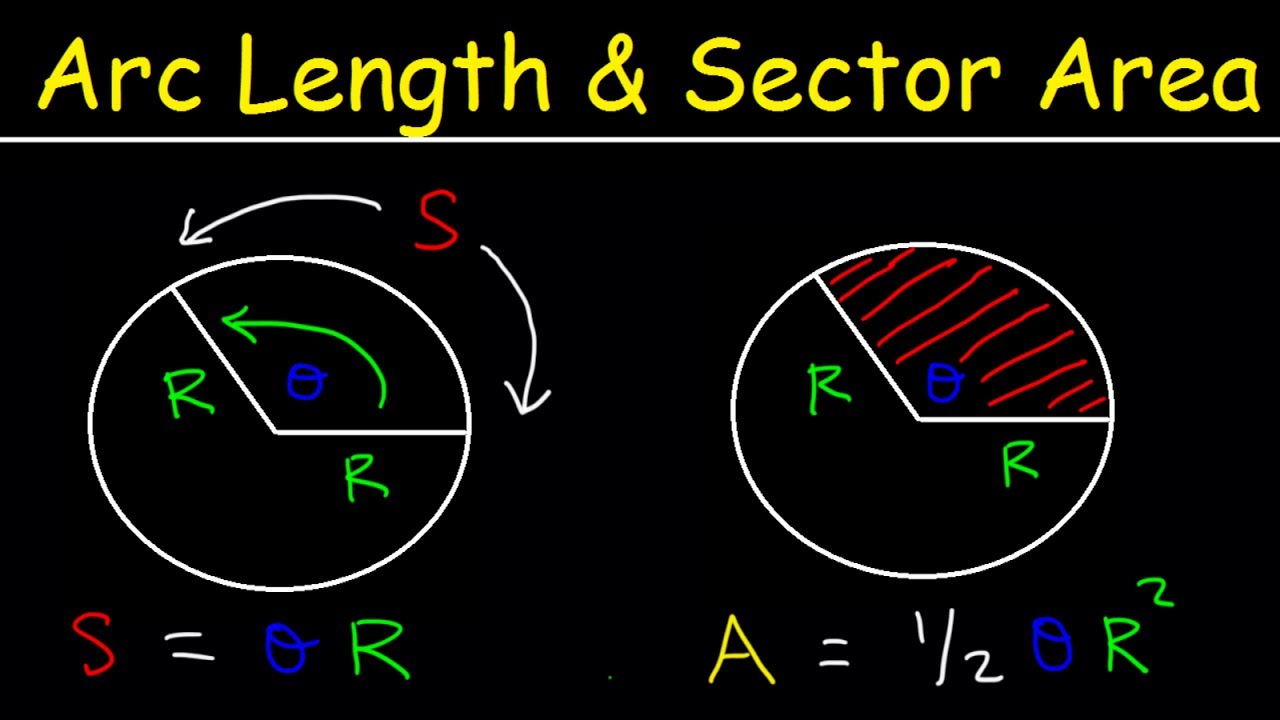
Arc Length of a Circle Formula - Sector Area, Examples, Radians, In Terms of Pi, Trigonometry
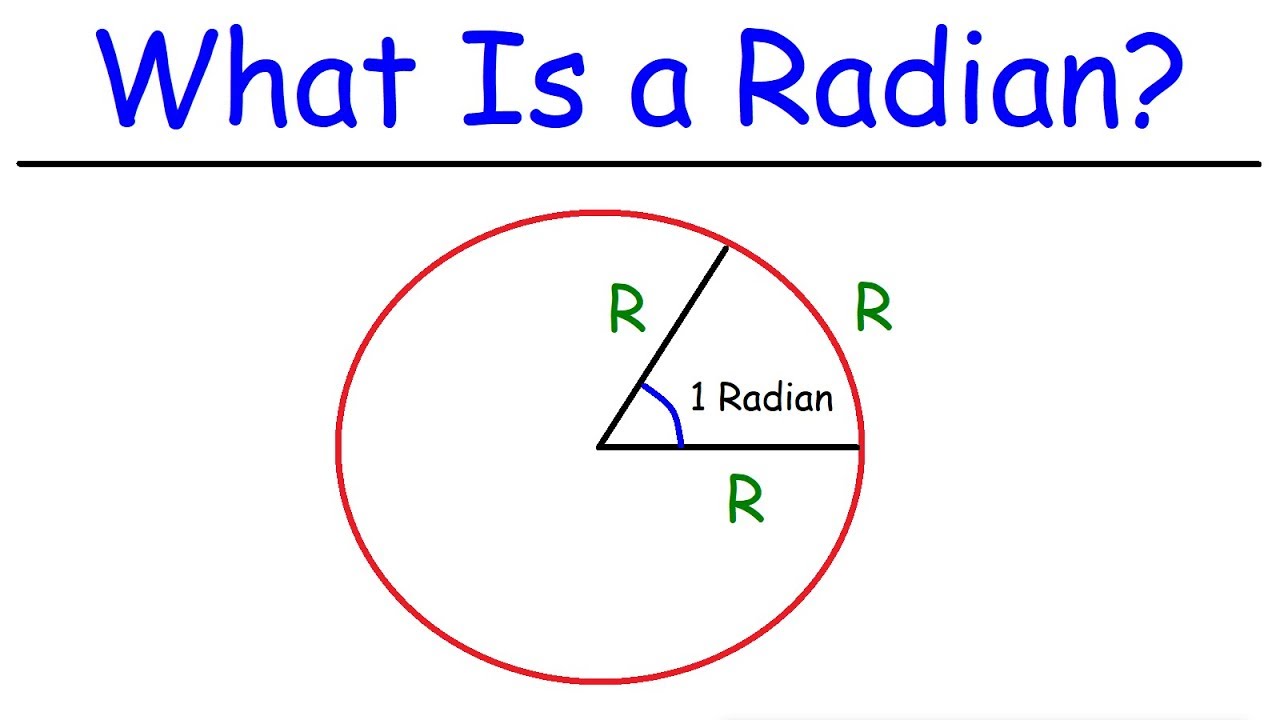
Trigonometry - What Exactly Is a Radian?

Arc Length and Area of a Sector | Formulas | Sample Problems | Trigonometry | Pre-Calculus

Rotational Motion: An Explanation, Angular Displacement, Velocity and Acceleration
5.0 / 5 (0 votes)
Thanks for rating: