What is the Schrödinger Equation? A basic introduction to Quantum Mechanics
TLDRThe video delves into the Schrödinger equation, a fundamental equation in quantum mechanics that describes the behavior of particles. It explores the life and work of Erwin Schrödinger, leading up to his development of the equation. The video provides an introductory overview of the equation, explaining its significance and how it forms the basis for understanding the universe at a quantum level. It also discusses the historical context, including the wave-particle duality and the contributions of Louis de Broglie and Einstein. The video aims to prepare viewers to engage with undergraduate-level quantum mechanics textbooks and appreciate the complex yet fascinating world of quantum mechanics.
Takeaways
- 📚 The Schrödinger equation is a fundamental equation in quantum mechanics, central to our understanding of the universe.
- 👶 Schrödinger was born in Vienna and excelled in mathematics and physics from a young age, leading to his development of the eponymous equation.
- 🌪️ De Broglie's thesis on wave-particle duality and Einstein's photoelectric effect inspired Schrödinger to develop a wave equation for particles.
- 🌊 The wave function in quantum mechanics is a complex function, with its modulus squared representing the probability density of finding a particle at a certain location.
- 📈 The time-independent Schrödinger equation leads to stationary states with sharply defined energies and no change in probability density over time.
- 🔢 The expectation value of the energy for a quantum state is given by the eigenvalue when the wave function is an eigenfunction of the Hamiltonian operator.
- 🎶 The linear superposition of quantum states allows for the description of a particle with uncertain energy, with probabilities given by the modulus squared of the coefficients.
- 🌀 Non-stationary states introduce uncertainty and time-dependence in observable properties, such as the probability density and position expectation value.
- 💡 The Schrödinger equation can be used to explain the stability of atoms and the emission of radiation during electronic transitions.
- 🌟 Schrödinger's work earned him a Nobel Prize and his equation is integral to the modern comprehension of particle physics.
- 🚀 The Schrödinger equation's applications extend to explaining phenomena such as quantum tunneling, crucial for understanding stellar processes.
Q & A
What is the Schrödinger equation?
-The Schrödinger equation is a fundamental equation in quantum mechanics that describes how the quantum state of a physical system changes with time. It is a partial differential equation that is central to our modern understanding of the universe and forms the basis for calculating various properties of particles and systems in quantum mechanics.
Who developed the Schrödinger equation?
-The Schrödinger equation was developed by Erwin Rudolph Joseph Alexander Schrödinger, an Austrian physicist, in 1926. Schrödinger's work on this equation earned him the Nobel Prize in Physics.
How does the Schrödinger equation relate to the wave-particle duality?
-The Schrödinger equation is a mathematical representation of the wave-particle duality concept, where particles such as electrons can exhibit both wave-like and particle-like behaviors. The equation describes the wave function of a particle, which can be used to calculate the probabilities of finding the particle in various states or positions, thus connecting the wave-like properties to measurable outcomes.
What is the significance of the wave function in quantum mechanics?
-The wave function in quantum mechanics is a mathematical function that provides information about a system's quantum state. It contains all the information needed to describe the system, including the probabilities of finding a particle in different locations or states. The modulus squared of the wave function represents the probability density, which is a key concept in understanding quantum phenomena.
What is the role of the Hamiltonian operator in the Schrödinger equation?
-The Hamiltonian operator in the Schrödinger equation is a differential operator that represents the total energy of the system, including both kinetic and potential energies. It plays a crucial role in the time-independent Schrödinger equation, which is used to find the eigenvalues and eigenfunctions that describe the stationary states of a quantum system.
What is the difference between the time-dependent and time-independent Schrödinger equations?
-The time-dependent Schrödinger equation describes the evolution of a quantum system's wave function over time, taking into account any changes in the system's potential energy. The time-independent Schrödinger equation, on the other hand, is used to find the stationary states of a system where the potential energy is constant. It is a simpler form that allows for the identification of the system's energy eigenvalues and corresponding eigenfunctions.
What is the physical interpretation of the complex coefficients in a linear superposition of quantum states?
-The complex coefficients in a linear superposition of quantum states represent the probabilities of measuring a particular energy eigenvalue. The modulus squared of each coefficient gives the probability that a measurement of the energy will yield the corresponding eigenvalue, and these probabilities must sum up to one, as required by the normalization condition.
How does the probability density of a quantum system change with time in a linear superposition of states?
-In a linear superposition of states, the probability density of a quantum system can change with time due to the oscillatory nature of the coefficients' exponential terms. This results in the probability density oscillating, indicating that the most likely location to find the particle changes over time, which is a characteristic of non-stationary states.
What is the relationship between the expectation value of energy and the energy eigenvalues in a quantum system?
-The expectation value of energy in a quantum system is the average value that would be obtained from measuring the energy of the system multiple times. For a system in a stationary state, the expectation value of energy is equal to the energy eigenvalue associated with that state. However, for a non-stationary state, which is a linear superposition of different energy eigenstates, the expectation value of energy is a weighted average of the energy eigenvalues based on the coefficients of the superposition.
How does the Schrödinger equation help explain the stability of atoms?
-The Schrödinger equation provides a framework for understanding the stationary states of electrons in atoms, which are associated with definite energy levels. It resolves the paradox of atomic stability by explaining that an electron in the ground state (lowest energy) does not emit radiation, as there is no lower energy state to transition to. It is only when an electron transitions between energy levels that radiation is emitted, which corresponds to the energy difference between the two levels.
What is the connection between the Schrödinger equation and the emission of light in atomic transitions?
-The Schrödinger equation can be used to calculate the energy levels of electrons in an atom and predict the frequencies of photons emitted during electronic transitions between these levels. The frequency of the emitted light corresponds to the energy difference between the two energy levels, as described by the equation E = hν, where E is the energy difference, h is Planck's constant, and ν is the frequency of the emitted photon.
Outlines
🌌 Introduction to Schrödinger's Equation
The video begins with an introduction to Schrödinger's Equation, a fundamental equation in quantum mechanics that forms the basis of our modern understanding of the universe. The aim is to provide an introductory overview, encouraging viewers to delve into quantum mechanics textbooks with newfound interest and readiness.
📚 Schrödinger's Early Life and Career
The narrative then delves into the life of Erwin Schrödinger, detailing his upbringing, education, and early career. It highlights his academic excellence, his initial work in experimental physics, and his various academic positions across Europe. Schrödinger's journey from a young physicist to a potential quantum mechanics pioneer is emphasized.
🌟 The Birth of Quantum Mechanics
The video discusses the pivotal moment in 1925 when Schrödinger encountered de Broglie's thesis on wave-particle duality, leading to his development of the quantum mechanical wave equation. It explains how Schrödinger's work on wave functions and the missing wave equation was influenced by the ideas of Einstein and de Broglie, and how it revolutionized physics.
📈 Understanding Classical Waves
A review of classical wave properties is provided, explaining how a simple progressive wave can be described using a cosine function. The video introduces wave number, angular frequency, and the general wave equation, highlighting the relationship between wave function and wave equation that Schrödinger considered in developing his theory.
🔬 The Development of Schrödinger's Wave Equation
The video outlines the challenge Schrödinger faced in creating a wave equation that could determine the wave function for any given situation. It discusses the assumptions made in formulating the equation, including consistency with de Broglie-Einstein postulates, the energy equation for a particle, and the requirement for linearity in the wave function.
🌀 The Complex Nature of Wave Functions
The video explores the concept of complex numbers and their role in quantum mechanics, particularly in wave functions. It explains how the modulus squared of a complex number represents a real, non-negative value, leading to Max Born's interpretation that it represents the probability of finding a particle at a particular location.
📊 Probability Distribution and Normalization
The discussion shifts to the probabilistic interpretation of the wave function, emphasizing that the wave function itself is not measurable but the modulus squared is. The concept of normalization is introduced, explaining how it ensures the total probability of finding a particle somewhere in space is one.
🧪 The Particle in a Box Example
A detailed example of a particle confined to a one-dimensional box is presented. The video explains how the time-independent Schrödinger equation can be solved to find the eigenfunctions and eigenvalues, leading to the quantization of energy levels and the concept of stationary states.
📈 Expectation Values and Quantum Uncertainty
The video discusses expectation values in quantum mechanics, drawing parallels with probability theory. It explains how the expectation value of a particle's position and energy can be calculated, and how quantum uncertainty gives rise to non-zero ground state energy in confined systems.
🌟 Stationary States and Eigenfunctions
The concept of stationary states and eigenfunctions is further explored, showing that these states have sharply defined energies and that the probability density does not change with time. The video also explains how the Hamiltonian operator is central to the energy eigenvalue equation and the concept of eigenfunctions.
🔄 Linear Superposition of Quantum States
The video concludes with an exploration of linear superpositions of quantum states, showing how any linear combination of eigenfunctions is also a solution to the Schrödinger equation. It discusses the physical meaning of the coefficients in a linear superposition and how they relate to the probabilities of measuring specific energy eigenvalues.
🌈 Non-Stationary States and Energy Uncertainty
The video delves into non-stationary states, which introduce uncertainty into the energy of a particle. It explains how the formation of a linear combination of states leads to oscillations in the probability density and position expectation value, highlighting the inherent uncertainty in energy due to the wave function being a combination of different energy eigenstates.
🌠 Link to Atomic Transitions and Radiation
The final part of the video draws a connection between the quantum mechanical analysis and the emission of radiation by atoms. It explains how the oscillation frequency of the charge distribution corresponds to the frequency of emitted light during electronic transitions, linking the particle in a box model to the full quantum mechanical theory of atoms.
🏆 Schrödinger's Contributions and Legacy
The video concludes by acknowledging Schrödinger's significant contributions to quantum mechanics and his Nobel Prize. It reflects on how Schrödinger's work has become central to our understanding of particle physics and the atom, and it ends with a quote from Schrödinger emphasizing the value of expressing thoughts through language.
Mindmap
Keywords
💡Schrodinger Equation
💡Wave-Particle Duality
💡Quantum States
💡Probability Density
💡Eigenfunctions and Eigenvalues
💡Normalization
💡Linear Superposition
💡Expectation Value
💡Heisenberg's Uncertainty Principle
💡Quantum Tunneling
💡Max Born's Probabilistic Interpretation
Highlights
The Schrödinger equation is introduced as one of the most important equations in physics, central to quantum mechanics and our understanding of the universe.
Erwin Schrödinger's early life and education, excelling in mathematics and physics, and his eventual development of the Schrödinger equation.
The development of the Schrödinger equation was influenced by the wave-particle duality theory proposed by Louis de Broglie.
Schrödinger's breakthrough in 1925, which ensured his place in the history of physics, was finding a missing wave equation for particles like electrons.
The general wave equation and its relation to wave function, frequency, and wavelength, which Schrödinger used as a basis for developing his quantum mechanical wave equation.
The assumptions made in constructing the Schrödinger equation, including consistency with the de Broglie-Einstein postulates and linearity in the wave function.
The derivation of the Schrödinger equation, including the introduction of imaginary numbers and the identification of the wave function's modulus squared as representing probability.
The significance of the Schrödinger equation in determining the wave function associated with a particle and the interpretation of the wave function as a probability density function.
The process of solving the Schrödinger equation, including the separation of variables technique and the concept of stationary states.
The application of the Schrödinger equation to a specific example: a particle in a one-dimensional box, also known as the infinite square well.
The quantization of energy in quantum systems, as demonstrated by the particle in a box example, where the energy can only take discrete values.
The normalization of the wave function to ensure that the total probability of finding the particle somewhere in space is one, and its implications for the physical interpretation of the wave function.
The use of probability theory in quantum mechanics to calculate expectation values and understand the statistical nature of quantum measurements.
The concept of eigenvalues and eigenfunctions in the context of the time-independent Schrödinger equation and their role in describing stationary states.
The linear superposition of quantum states, which allows for the construction of a general solution to the Schrödinger equation as a combination of energy eigenstates.
The physical interpretation of the coefficients in a linear superposition of quantum states, representing the probability of measuring a particular energy eigenvalue.
The time-dependent behavior of quantum systems, such as the oscillation of probability density and position expectation value in a linear superposition of states.
The link between the Schrödinger equation and the emission of radiation in atomic transitions, as predicted by Bohr's model of the atom.
Schrödinger's contribution to the understanding of the atom and his Nobel Prize recognition, emphasizing the importance of his work in modern physics.
Transcripts
Browse More Related Video

24. Quantum Mechanics VI: Time-dependent Schrödinger Equation

Quantum Mechanics - Part 2: Crash Course Physics #44

What Is Quantum Mechanics Explained

How Schrodinger Came Up With His Famous Equation (But EASIER)

The SIMPLEST Explanation of QUANTUM MECHANICS in the Universe!
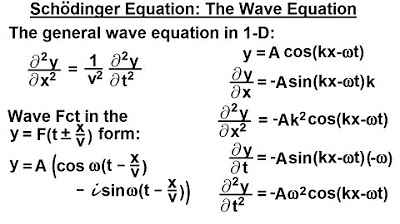
Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (3 of 92) The Wave Equation
5.0 / 5 (0 votes)
Thanks for rating: