Piecewise Functions - Limits and Continuity | Calculus
TLDRThe transcript discusses piecewise functions and their limits. It explains how to find the value of a function and its limits at certain points by using the appropriate piecewise rule. The process involves substituting values into the function's equations and comparing one-sided limits to determine if the overall limit exists. An example is given where the constant 'c' is found to make a function continuous at x=2, demonstrating how to equate the function's expressions at the point of discontinuity.
Takeaways
- 📈 The piecewise function f(x) is defined with different expressions for x < 2, 2 ≤ x ≤ 4, and x > 4.
- 🔄 When approaching 2 from the left, the function f(x) = 5x + 3 is used, leading to a limit of 13 as x -> 2 (from the left).
- 🔄 For the right approach of 2, f(x) = 2x^2 + 5, which also results in a limit of 13 as x -> 2 (from the right).
- 🔄 The limit as x -> 2 from either side is 13, since the left and right limits are equal.
- 🚫 The limit as x -> 4 from either side does not exist because the left-sided limit (37) is not equal to the right-sided limit (47).
- 🎯 The value of f(2) is 13, as determined by the piecewise function for 2 ≤ x ≤ 4.
- 🔄 For another piecewise function, the limit as x -> 1 from both sides is 2, since the left-sided limit (7(1) - 5 = 2) equals the right-sided limit (3(1)^2 - 1 = 2).
- 🎯 The value of f(1) is 5, as specified by the function definition for x = 1.
- 🔄 The limit as x -> 3 from either side does not exist due to mismatched left-sided (24) and right-sided (31) limits.
- 🎯 The value of f(3) is 24, using the piecewise function for x ≤ 3.
- 🔧 To make the function continuous at x = 2, the constant c must be equal to 3, by setting the two expressions for f(x) equal to each other at x = 2 and solving for c.
Q & A
What is the value of the limit of the function f(x) as x approaches 2 from the left side?
-The limit of the function f(x) as x approaches 2 from the left side is 13.
Which expression of the piecewise function is used to calculate the limit as x approaches 2 from the right side?
-To calculate the limit as x approaches 2 from the right side, the expression 2x^2 + 5 of the piecewise function is used.
What is the limit of f(x) as x approaches 2 from either side?
-The limit of f(x) as x approaches 2 from either side is 13.
What is the value of f(2) according to the piecewise function?
-The value of f(2) is 13, as per the piecewise function.
What is the limit of the function f(x) as x approaches 4 from the left side?
-The limit of f(x) as x approaches 4 from the left side is 37.
Why does the limit of f(x) as x approaches 4 not exist?
-The limit of f(x) as x approaches 4 does not exist because the one-sided limits are different. From the left side, the limit is 37, and from the right side, it's 47.
What is the value of f(4) in the piecewise function?
-The value of f(4) in the piecewise function is 47.
How is continuity at x = 2 ensured in the function involving the constant c?
-Continuity at x = 2 is ensured by setting the expressions on either side of x = 2 equal to each other at that point and solving for the constant c, which is found to be 3.
What is the limit of f(x) as x approaches 1 from either side?
-The limit of f(x) as x approaches 1 from either side is 2.
What discrepancy occurs in the limits as x approaches 3, and what does it imply about the function's continuity at that point?
-The discrepancy occurs as the left-sided limit is 24 and the right-sided limit is 31 as x approaches 3, implying that the function is not continuous at that point since the limits do not match.
Outlines
📚 Analysis of Piecewise Functions and Limits
This paragraph discusses the concept of piecewise functions and their limits. It introduces a piecewise function defined differently for ranges of x values. The limit of the function as x approaches 2 from the left is calculated using the appropriate piece of the function (5x+3 for x<2), resulting in the value 13. The limit from the right side and the value of f(2) are also determined using the respective parts of the function, both yielding the value 13. The limit as x approaches 4 is then examined, with different results from the left (37) and right (47), leading to the conclusion that the limit does not exist. The value of f(4) is also calculated to be 47. The explanation involves selecting the correct part of the function based on the value of x and understanding the concept of one-sided limits and continuity.
📈 Evaluation of Piecewise Functions and Their Behavior
This paragraph delves into the evaluation of another piecewise function and its behavior around certain points. The function is defined for different ranges of x values, with specific values assigned for x equals 1 and x greater than 3. The left and right limits as x approaches 1 are calculated, both resulting in the value 2, indicating the function is continuous at x=1. The value of f(1) is determined to be 5. The limits as x approaches 3 from both sides are then examined, with the left side yielding 24 and the right side not existing due to a mismatch in values. The value of f(3) is calculated using the appropriate part of the function, resulting in 24. The paragraph concludes with a method to find the constant c that makes the function continuous at x=2, which is found to be 3.
Mindmap
Keywords
💡Piecewise Function
💡Limit
💡Continuity
💡Domain
💡Function Value
💡One-Sided Limits
💡Two-Sided Limit
💡Constant
💡Substitution
💡Graph
💡Discontinuity
Highlights
The piecewise function f(x) is defined with different expressions for x < 2, 2 ≤ x ≤ 4, and x > 4.
For x approaching 2 from the left, f(x) is calculated using the first part of the piecewise function, 5x + 3.
The limit of f(x) as x approaches 2 from the left side is found to be 13 by substituting x with 1.99.
When approaching 2 from the right, the function is described by the second part, 2x^2 + 5, yielding a limit of 13.
The limit from both sides of f(x) at x=2 is the same, confirming it to be 13.
The value of f(2) is determined to be 13 using the second part of the piecewise function.
For x approaching 4 from the left, the function is represented by 2x^2 + 5, with a limit of 37.
The limit from the right side of f(x) as x approaches 4 is found to be 47 using the third part of the function.
The limit as x approaches 4 from either side does not exist because the left and right one-sided limits are not equal.
The value of f(4) is calculated to be 47 using the third part of the piecewise function.
Another piecewise function is introduced with different expressions for x < 1, 1 ≤ x ≤ 3, and x > 3.
The left-sided limit as x approaches 1 from the left is 2, using the first part of the new piecewise function.
The right-sided limit as x approaches 1 from the right is also 2, using the second part of the function.
The limit as x approaches 1 from either side is 2, since the left and right limits are equal.
The value of f(1) is determined to be 5 based on the function definition at x equals 1.
For x approaching 3 from the left, the function is described by the second part, 3x^2 - x, with a limit of 24.
The right-sided limit as x approaches 3 from the right does not match the left-sided limit, so the overall limit does not exist.
The value of f(3) is calculated to be 24 using the second part of the piecewise function.
A function f(x) is defined with a break at x=2, where the function changes from cx + 3 to 3x + c.
To ensure continuity at x=2, the two parts of the function must be equal, leading to an equation to solve for c.
Solving for c results in c being equal to 3, which makes the function continuous at x=2.
Transcripts
Browse More Related Video

BusCalc 02 Limits and Continuity

Math 11 - Sections 1.1-1.2

AP Calculus AB Crash Course Day 3 - Limits, Continuity, and Differentiation

Example: When is a Piecewise Function Continuous?

3 Step Continuity Test, Discontinuity, Piecewise Functions & Limits | Calculus
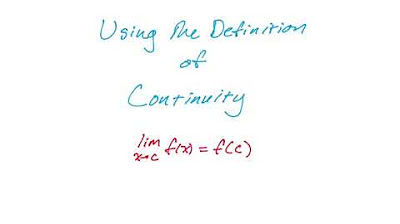
Using the Definition of Continuity in Calculus
5.0 / 5 (0 votes)
Thanks for rating: