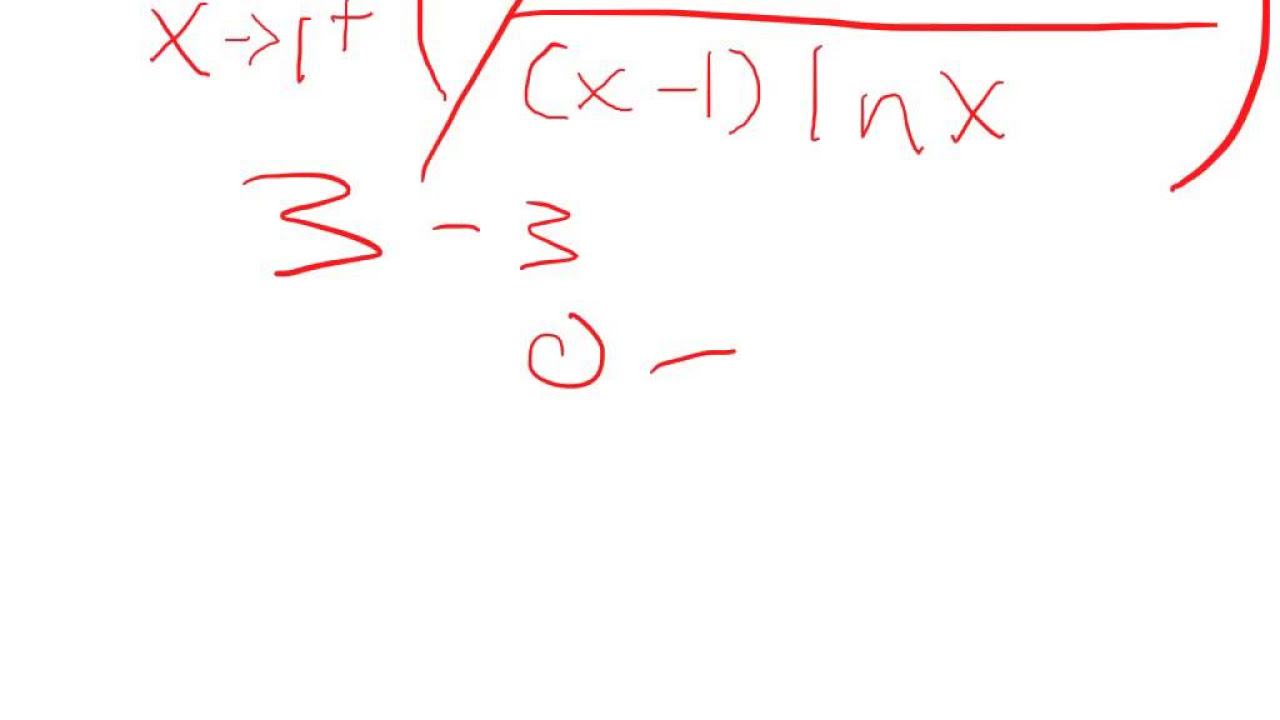THE FACT

blackpenredpen
18 May 201714:47
EducationalLearning
32 Likes 10 Comments

TLDRIn this educational video, the instructor explores the concept of a well-known limit in calculus, often encountered in sequence and series sections. The script guides viewers through the process of calculating the limit as X approaches infinity of (1 + a/X) raised to the power of BX, using logarithmic properties and L'Hôpital's rule to resolve indeterminate forms. The instructor simplifies the process by introducing a 'fact' formula, e^a, to quickly determine the limit's value, demonstrating its application with an example. The video is aimed at students who need to understand or quickly calculate such limits, emphasizing the importance of showing all steps for a complete solution.

Takeaways
  • 📘 The video discusses a famous limit equation frequently encountered in Calculus, particularly in sequences and series sections.
  • 🧮 The equation in focus is the limit as X approaches infinity of (1 + a/X) raised to the BX power.
  • 🔍 The speaker explains that this limit is often referred to as 'the fact' in their Calculus class.
  • 📝 A key approach to solving this limit involves taking the natural logarithm (Ln) on both sides of the equation to simplify the expression.
  • 🔄 By applying the logarithm properties, the exponent can be moved to the front, converting the limit into a more manageable form.
  • 🚧 The equation initially results in an indeterminate form (Infinity times 0), requiring further steps to resolve.
  • ⚙️ To overcome the indeterminate form, the speaker applies L'Hôpital's Rule after rearranging the equation.
  • ✏️ The final limit is found to be e^(a * B), where 'a' and 'B' are constants defined in the original equation.
  • 📊 The speaker uses a specific example, where a = -2 and B = 3, to illustrate how to apply 'the fact' for quick calculations.
  • 🎓 The speaker emphasizes that while 'the fact' can be used for quick answers, it's important to show all the steps in a formal proof or detailed solution.
Q & A

  • What is the main topic of the video script?

    -The main topic of the video script is the calculation of a specific limit as X approaches infinity, which is a common equation in calculus, particularly in the sequence and series section.

  • What is the 'fact' referred to in the script?

    -The 'fact' referred to in the script is a shorthand for a specific limit formula that the instructor uses to simplify the process of solving such limits in calculus.

  • What is the indeterminate form encountered when plugging in infinity into the limit?

    -The indeterminate form encountered is '1 to the power of infinity', which does not provide a clear answer and requires further work to resolve.

  • Why is taking the natural logarithm (Ln) of both sides a common approach when dealing with limits of the form 1 + a/x raised to the BX power?

    -Taking the natural logarithm of both sides is a common approach because it simplifies the expression by bringing the exponent to the front, making it easier to handle the limit as X approaches infinity.

  • What is the purpose of applying L'Hôpital's Rule in this context?

    -L'Hôpital's Rule is applied to handle the indeterminate form '0/0' that arises after simplifying the limit expression, allowing for the differentiation of the numerator and denominator to find the limit.

  • What is the final result of the limit as X approaches infinity of (1 + a/X)^(BX)?

    -The final result of the limit is e^a, where e is the base of the natural logarithm.

  • How does the sign of B affect the initial evaluation of the limit?

    -The sign of B does not affect the initial evaluation because whether B is positive or negative, the result of 1 + a/infinity raised to the B*infinity power is still an indeterminate form of infinity.

  • What is the significance of identifying A and B values in the limit equation?

    -Identifying A and B values is significant because they are the coefficients that will be used in the final formula e^a to determine the limit's value.

  • How can the 'fact' be used to quickly find the value of a similar limit without showing all the steps?

    -The 'fact' can be used by identifying the A and B values in the given limit equation and directly applying the formula e^a to quickly find the limit's value without going through the entire derivation process.

  • What is the derivative of 1/x with respect to x?

    -The derivative of 1/x with respect to x is -1/x^2, which is a standard result in calculus that is used in the process of differentiating the numerator and denominator when applying L'Hôpital's Rule.

Outlines
00:00
📚 Introduction to a Famous Limit Equation

The script begins with an introduction to a well-known limit equation, often encountered in calculus, particularly in the context of sequences and series. The presenter aims to derive a formula for the limit as X approaches infinity of (1 + a/X)^(BX). This formula is referred to as 'the fact' in the presenter's calculus class and serves as a quick reference for students. The presenter provides an example with specific values for a and B to illustrate how to apply this formula, emphasizing the importance of understanding the steps involved in deriving the formula for those who may need to calculate it from scratch.

05:03
🔍 Analyzing the Limit with Logarithms

The second paragraph delves into the process of evaluating the limit by taking the natural logarithm of both sides, transforming the expression into a more manageable form. The presenter explains the use of logarithmic properties to simplify the equation, leading to an indeterminate form of infinity times zero. The focus then shifts to handling this indeterminate form by manipulating the equation to apply L'Hôpital's Rule, which is a standard technique for solving such limits. The presenter guides the audience through the algebraic and calculus steps necessary to simplify the expression and prepare it for the application of the rule.

10:05
🎓 Applying L'Hôpital's Rule and Finding the Limit

In the final paragraph, the presenter applies L'Hôpital's Rule to the simplified expression, resulting in a straightforward calculation that leads to the conclusion that the limit is e^a. The presenter emphasizes the importance of recognizing the need for this rule when faced with an indeterminate form and demonstrates how to correctly differentiate the numerator and denominator. After applying the rule, the presenter simplifies the expression to arrive at the final answer, e^a, which is referred to as 'the fact' for quick reference in future calculations. The script concludes with an example that illustrates how to quickly apply this derived formula to find the value of a similar limit, highlighting the efficiency of using 'the fact' for students in their calculus studies.

Mindmap
Keywords
💡Limit
In the context of the video, 'limit' refers to a fundamental concept in calculus where one evaluates the behavior of a function as its input approaches a certain value, in this case, as 'X' approaches infinity. The video focuses on a specific type of limit involving exponential functions, which is central to understanding the theme of the video.
💡Indeterminant Form
The term 'indeterminant form' is used to describe a situation in calculus where the direct substitution of a value results in an ambiguous expression, such as 0/0 or ∞/∞. The video script mentions this when discussing the initial evaluation of the limit, which leads to the need for further mathematical manipulation to find a determinate answer.
💡Logarithm
A 'logarithm' is a mathematical function that is the inverse of exponentiation, used to solve equations involving unknown exponents. In the video, the logarithm function is applied to both sides of the limit equation to simplify the expression and make it easier to evaluate, illustrating its utility in solving complex limit problems.
💡Continuous Function
A 'continuous function' is one where there are no breaks, jumps, or asymptotic behavior in its graph. The video mentions the continuity of the logarithm function, which allows for the application of logarithmic properties without disrupting the limit's evaluation process.
💡L'Hôpital's Rule
L'Hôpital's Rule is a theorem in calculus that provides a method for evaluating limits of the form 0/0 or ∞/∞ by taking the derivatives of the numerator and denominator. The video script describes using this rule to resolve the indeterminant forms that arise when evaluating the limit of the given function as 'X' approaches infinity.
💡Derivative
The 'derivative' of a function measures the rate at which the function's output changes with respect to its input. The video explains how to find the derivative of the function inside the limit to apply L'Hôpital's Rule, demonstrating the process of differentiation as part of evaluating the limit.
💡Chain Rule
The 'chain rule' is a fundamental principle in calculus for differentiating composite functions. The video script refers to this rule when differentiating the function inside the limit, which involves a composition of functions, to apply L'Hôpital's Rule correctly.
💡Exponential Function
An 'exponential function' is a mathematical function where the variable is in the exponent. The video's main theme revolves around evaluating a specific limit involving an exponential function, which is a common occurrence in calculus, especially in sequences and series.
💡Sequence
A 'sequence' is an ordered list of numbers or terms. The video mentions that the type of limit discussed is often encountered in the study of sequences, indicating its relevance in analyzing the convergence or divergence of sequences.
💡Series
A 'series' is the sum of the terms of a sequence. The video script notes that the limit in question is frequently seen in the context of series, particularly when determining the convergence of infinite series.
Highlights

Introduction to a famous limit equation often encountered in calculus, especially in the sequence and series section.

The limit equation is presented as \( \lim_{{x \to \infty}} (1 + \frac{a}{x})^{Bx} \) and is referred to as 'the fact' for easy reference in class.

Initial attempt to evaluate the limit by plugging in infinity for x, resulting in an indeterminate form of either positive or negative infinity.

Explanation of the logarithmic approach to handle the indeterminate form by taking the natural logarithm of both sides of the equation.

Application of logarithmic properties to simplify the expression, bringing the power to the front and preparing for differentiation.

Identification of the indeterminate form \( \infty \times 0 \) after simplification, necessitating further work to find the limit.

Use of L'Hôpital's rule to resolve the \( \frac{0}{0} \) indeterminate form by differentiating the numerator and denominator.

Derivation of the expression for the limit using L'Hôpital's rule, leading to a simplified form involving constants a and B.

Final simplification of the limit to \( e^a \) after canceling out terms and recognizing the exponential function.

Emphasis on the importance of showing all steps when asked to demonstrate the work, including algebraic manipulations and calculus principles.

Introduction of 'the fact' as a quick reference for students to find the value of similar limits without showing all steps.

Demonstration of how to use 'the fact' with an example to quickly determine the limit of \( (1 - \frac{2}{n})^{3n} \) as \( n \to \infty \).

Explanation of the variable substitution from n to x for generality in limit problems and the application of 'the fact'.

Identification of the values of a and B in the example, which are -2 and 3, respectively, for the application of 'the fact'.

Calculation of the limit using 'the fact', resulting in \( e^{-2} \times 3 \) and further simplification to \( \frac{1}{e^6} \).

Highlighting the convenience of using 'the fact' for quick calculations in series or sequence situations in calculus.

Reiteration of the importance of understanding the full derivation process for academic purposes, despite the convenience of 'the fact'.

Transcripts

Browse More Related Video

Using L'Hopital's Rule to show that exponentials dominate polynomials

Zero-Bounded Limit Theorem (with example)

Limits of Logarithmic Functions | Calculus

finally 0^0 approaches 0 after 6 years!

Ryan and Nick do L'hopital's rule

Example of Using L'Hopital's Rule Twice to Evaluate a Limit

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Calculus LimitsSequence SeriesLogarithm PropertiesIndeterminate FormsL'Hôpital's RuleEducational ContentMathematics TutorialLimit CalculationInfinity ConceptsEuler's Number