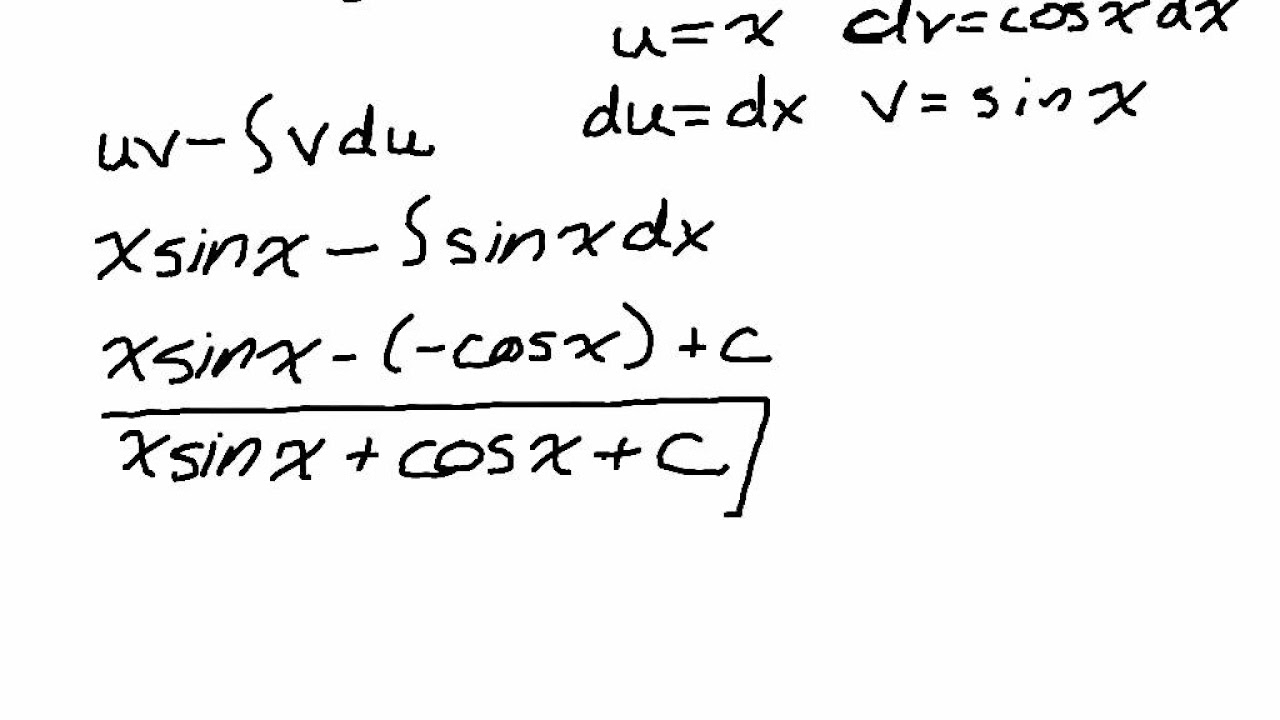Lesson 15 - Integration By Parts (Calculus 1 Tutor)
TLDRIn this instructional video, the presenter introduces the concept of integration by parts, a fundamental technique in calculus for integrating products of functions. The video begins by contrasting this method with integration by substitution and emphasizes the importance of recognizing when integration by parts is the appropriate approach. The presenter then illustrates the technique with a specific example, showing how to break down the integral into parts (u and dv), calculate the derivative of u (du), and apply the integration by parts formula. The goal is to transform a complex integral into a more manageable form, ultimately solving it through this clever rearrangement.
Takeaways
- 📚 Integration by parts is a fundamental technique in calculus for solving integrals.
- 🔍 Initially, it may seem challenging, but with examples and practice, it becomes more understandable.
- 👀 The formula for integration by parts is ∫u dv = uv - ∫v du.
- 📝 To apply this method, identify 'u' and 'dv' from the given integral such that 'u' is a function of 'x' and 'dv' is the differential part.
- 🤔 When 'u' is chosen, its derivative 'du' should be simpler or easier to handle than the original integral.
- 🌟 The integral ∫x * e^(2x) dx is an example where integration by parts is more effective than substitution.
- 📊 For the example given, let 'u' = x, which leads to du = dx, and 'dv' = e^(2x) dx, which simplifies to 'v' = (1/2)e^(2x) when integrated.
- 🧠 The process involves breaking down the integral into manageable parts and using the integration by parts formula to solve.
- 📝 The derivative of 'u' with respect to 'x' (du) must be calculated to complete the integration by parts formula.
- 🔄 The technique often requires practice and problem-solving to become proficient in its application.
- 📈 Understanding the concept and process of integration by parts is crucial for tackling more complex integrals in calculus.
Q & A
What is the topic of discussion in this section of the class?
-The topic of discussion in this section is integration by parts, a technique of integration.
What is the formula for integration by parts?
-The formula for integration by parts is ∫u dv = uv - ∫v du.
What is the purpose of using integration by parts?
-Integration by parts is used when the integral cannot be easily solved by other techniques, such as when the function is indestructible or cannot be canceled out through substitution.
How does the process of integration by parts begin?
-The process begins by defining 'u' as one part of the integral and 'dv' as the rest, including the differential 'dx'.
What is the significance of the function e^x in this context?
-The function e^x is significant because it is an indestructible function; its derivative is the same as the function itself, making it difficult to integrate using simple substitution.
What was the integral example given in the script?
-The integral example given was ∫x * e^(2x) dx.
Why is substitution not effective for the given integral example?
-Substitution is not effective because the function e^(2x) cannot be canceled out, and the derivative of x would result in a term that includes x, which cannot be eliminated.
What is the next step after defining 'u' and 'dv'?
-After defining 'u' and 'dv', the next step is to calculate the derivative of 'u' with respect to x (du/dx) to find 'du'.
What is the derivative of 'u' as defined in the example?
-In the example, 'u' is defined as x, so the derivative of 'u' with respect to x (du/dx) is 1.
How does the process of integration by parts help in solving the integral?
-Integration by parts allows us to break the integral into simpler parts, calculate the derivative of one part (du), and rewrite the integral in a form that can be solved using the integration by parts formula.
What is the main challenge when learning integration by parts?
-The main challenge when learning integration by parts is identifying the correct 'u' and 'dv' to use in the formula, which requires practice and understanding of the technique.
Outlines
📘 Introduction to Integration by Parts
This paragraph introduces the concept of integration by parts, a technique in calculus for integrating functions. The speaker explains that while previously discussing integration by substitution, integration by parts is a fundamental method that may initially seem challenging but becomes manageable once the formula is understood. The formula shared is ∫(uv')dx = uv - ∫(vdu), emphasizing that this is the sole formula to remember for this technique. The speaker intends to clarify how to apply this formula through problem-solving, starting with an example of ∫(x * e^(2x))dx. The paragraph highlights the limitations of substitution in this case due to the indestructible nature of the function e^x and the inability to cancel out the x term through substitution. The technique of integration by parts is presented as a solution to tackle such integrals by breaking them into two cleverly defined parts.
📘 Defining u and dv in Integration by Parts
In this paragraph, the speaker delves into the process of defining u and dv for the integration by parts technique. The speaker chooses u to be x and dv to be 2x dx for the given example integral. The rationale behind this choice is to express the integral in terms of u times dv, which is the foundation of the integration by parts formula. The speaker emphasizes that the goal is to break down the integral into manageable parts where u represents a portion of the integrand and dv is the remainder, including the differential dx. The paragraph concludes with the calculation of du, the derivative of u with respect to x, which in this case is 1, hence du equals dx.
Mindmap
Keywords
💡Integration by Parts
💡Integration by Substitution
💡Indestructible Function
💡Derivative
💡Integral
💡Formula
💡u and dv
💡Differential
💡Simplify
💡Canceling Out
💡Tricky
Highlights
The class introduces the technique of integration by parts, a core method in integration.
Integration by parts may initially seem difficult, but becomes manageable once you understand what to look for in problems.
The main formula for integration by parts is given as ∫u dv = uv - ∫v du.
The formula is simple but requires practice to master its application.
The example of ∫x * e^(2x) dx is used to illustrate the application of integration by parts.
Substitution might not work for certain integrals, such as the example given, due to the nature of the function.
Integration by parts was invented as a solution for integrals that cannot be solved through substitution.
The technique involves breaking the integral into two different parts, cleverly defined as u and dv.
The goal is to express the integral in terms of ∫u dv, which allows the use of the integration by parts formula.
In the example, u is chosen to be x and dv is chosen to be e^(2x) dx to facilitate the integration process.
The choice of u and dv is critical for the success of the integration by parts method.
Once u and dv are defined, the next step is to calculate du, which is the derivative of u with respect to x.
For the example, du/dx equals 1, simplifying the process.
Integration by parts is a powerful tool for tackling complex integrals that do not yield to simpler methods.
The method requires understanding and practice to become proficient in its application.
The class aims to demystify integration by parts and equip students with the skills to apply it effectively.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: