Two masses hanging from a pulley | Forces and Newton's laws of motion | Physics | Khan Academy
TLDRThe video script discusses an efficient method for solving systems of objects with shared acceleration, emphasizing the importance of distinguishing between external and internal forces. By treating the system as a single entity and considering only external forces, the acceleration is determined by dividing the net external force by the total mass. The example provided involves a five-kilogram and a three-kilogram mass connected by a rope, illustrating how to find the system's acceleration and the tension in the string. The script highlights the need for careful application of the concept to individual objects, considering the direction of acceleration for each.
Takeaways
- 📚 The problem-solving approach for systems can be simplified by treating them as a single entity when the objects involved have the same magnitude of acceleration.
- 🔢 To find the magnitude of acceleration for a system, divide the net external force acting on the system by the total mass of the system.
- ⚖️ Newton's second law can be applied in two ways: the traditional method solving for each object individually or the simplified method for systems with shared acceleration.
- 🎯 When calculating the net external force, consider only forces exerted by objects outside the system, ignoring internal forces as they cancel each other out.
- 🌐 The force of gravity acts on all masses in the system and should be included in the calculation, with its direction taken into account when determining the sign.
- 🔄 The tension in the rope connecting the masses is an internal force and does not affect the calculation of the system's overall acceleration.
- 👉 The direction of forces is crucial; forces propelling the system forward are considered positive, while those opposing the motion are negative.
- 🔄 When finding the acceleration of individual masses, remember to apply the correct sign based on the direction of their motion.
- 🧠 Understanding the concept of shared acceleration among objects in a system is key to applying this simplified method effectively.
- 🔍 If the problem requires finding individual tensions, revert to the traditional application of Newton's second law, considering the specific forces acting on each object.
- 📈 The tension in the string should be less than the force of gravity acting on the five-kilogram mass to ensure it accelerates downward as described by the system's calculated acceleration.
Q & A
What are the two methods mentioned for solving systems problems?
-The hard way involves solving Newton's second law for each box individually and then combining them to get two equations with two unknowns. The easy way is to find the net external force acting on the system and divide it by the total mass of the system to quickly get the magnitude of the acceleration of the objects in the system.
Why is the algebraic sign of the forces important when using the easy method?
-The algebraic sign of the forces is important because it helps determine the direction of the forces relative to the positive direction of motion. Forces in the direction of motion are considered positive, while forces opposite to the direction of motion are considered negative. This distinction is crucial for accurately calculating the net force and, subsequently, the acceleration of the system.
What is the condition that allows the system to be treated as a single object with a single total mass?
-The system can be treated as a single object with a single total mass when all objects within the system are required to move with the same magnitude of acceleration. This means that internal forces, such as tension in a rope connecting two masses, cancel each other out, and only external forces are considered in the calculation.
How do you calculate the net force acting on the system?
-To calculate the net force acting on the system, you sum up all the external forces acting on the objects within the system. This typically includes the force of gravity on each object. Forces that propel the system forward are considered positive, while forces that resist the motion are considered negative.
What is the total mass used to find the acceleration of the system?
-The total mass used to find the acceleration of the system is the sum of all the individual masses within the system. In the given example, it is the sum of the five-kilogram mass and the three-kilogram mass, which equals eight kilograms.
How do you find the acceleration of an individual object within the system?
-To find the acceleration of an individual object, you must apply the correct sign to the acceleration based on the direction of motion for that specific object. While the magnitude of the acceleration is the same for all objects in the system, the direction can be positive or negative depending on whether the object is accelerating in the positive or negative direction of motion.
What is the relationship between the tension in the rope and the force of gravity on the three-kilogram mass?
-The tension in the rope must be less than the force of gravity on the three-kilogram mass. This is because the tension is the internal force that resists the motion, while the force of gravity is the external force that tries to prevent the system from moving. The five-kilogram mass can only accelerate downward if the tension is less than the gravitational force.
How can you find the tension in the string after knowing the system's acceleration?
-Once the system's acceleration is known, you can find the tension in the string by applying Newton's second law to an individual object within the system. You would consider the net force on the object, including the tension and the force of gravity, and set it equal to the mass of the object multiplied by its acceleration, with the correct signs for direction.
Why are internal forces not included when calculating the net force on the system?
-Internal forces are not included in the calculation because they cancel each other out when the system is considered as a single object. Each internal force is opposed by another force within the system, so they do not contribute to the net force that causes the system to accelerate or decelerate.
What is the significance of treating the system as a single object?
-Treating the system as a single object simplifies the calculation of the net force and the acceleration of the system. It allows us to ignore the internal forces and focus only on the external forces and the total mass, making it easier to find the overall acceleration of the system.
How does the method of treating the system as a single object relate to Newton's second law?
-The method of treating the system as a single object is an application of Newton's second law. It considers the entire system as one entity with a total mass and net external forces acting upon it. By dividing the net external force by the total mass, we find the common acceleration experienced by all objects within the system.
Outlines
📚 Introduction to Solving Systems of Motion
In this introductory paragraph, the instructor sets the stage for solving systems problems by contrasting the hard and easy methods. The hard way involves applying Newton's second law individually to each box, leading to a system of equations, while the easy way simplifies the process by using the net external force and total mass to quickly find the magnitude of acceleration. The key takeaway is that the easy method only works when all objects in the system share the same magnitude of acceleration, as exemplified by the scenario with the five-kilogram and three-kilogram masses connected by a rope. The paragraph emphasizes the importance of understanding the distinction between external and internal forces and how they affect the system's acceleration.
🔢 Calculating Acceleration and Understanding Force Directions
This paragraph delves into the specifics of calculating the system's acceleration and the significance of force directions. The instructor explains how to find the acceleration of the five-kilogram box by considering the net external force (gravity) and the total mass of the system (eight kilograms), resulting in an acceleration of 2.45 meters per second squared. The discussion then moves to the individual accelerations of the boxes, highlighting that the five-kilogram box would have a negative acceleration while the three-kilogram box would have a positive one. The paragraph also touches on how to find the tension in the string using Newton's second law after obtaining the system's acceleration. The main points include the calculation of acceleration for a system and individual components, the concept of positive and negative forces relative to the direction of motion, and the method to determine tension in a system.
Mindmap
Keywords
💡Newton's second law
💡External forces
💡Internal forces
💡Acceleration
💡Tension
💡System
💡Magnitude
💡Positive and negative directions
💡Rope and pulley system
💡Mass
💡Canceling out
Highlights
Instructor introduces a system of problems with a hard and easy way to solve them.
The hard way involves solving Newton's second law for each box individually and combining the results.
The easy way to find the magnitude of acceleration is by using the net external force divided by the total mass of the system.
This method assumes that all objects in the system have the same magnitude of acceleration.
An example system includes a five-kilogram mass tied to a rope connected to a three-kilogram mass.
The rope ensures that the masses move with the same acceleration, preventing it from breaking.
External forces are forces exerted on the system from objects outside the system.
The force of gravity on the five-kilogram mass is an external force and is calculated as 5 kg * 9.8 m/s^2.
The force of gravity on the three-kilogram mass is an external force that opposes the motion of the system and is subtracted from the total force.
Internal forces, such as tension, cancel each other out and are not included in the calculation of system acceleration.
The total mass of the system is the sum of the individual masses, which is 8 kg in this case.
The calculated acceleration of the system is 2.45 m/s^2.
When finding the acceleration of individual masses, the direction of acceleration must be considered, with negative and positive signs applied accordingly.
To find the tension in the string, Newton's second law can be applied to each mass individually, considering the net force on that mass.
The tension in the string is found to be 36.75 Newtons, which is less than the force of gravity.
The method of treating the system as a single object is a quick way to solve for the magnitude of the system's acceleration.
Internal forces cancel out when considering the system as a single object, as they are applied internally and opposed to each other.
The video provides an alternative solution to these problems using the hard way, demonstrating the same principles.
Transcripts
Browse More Related Video

Masses on incline system problem | Forces and Newton's laws of motion | Physics | Khan Academy

2015 AP Physics 1 free response 1b

Newton's Laws of Motion and Forces

College Physics 1: Lecture 19 - Interacting Objects, Ropes, and Pulleys
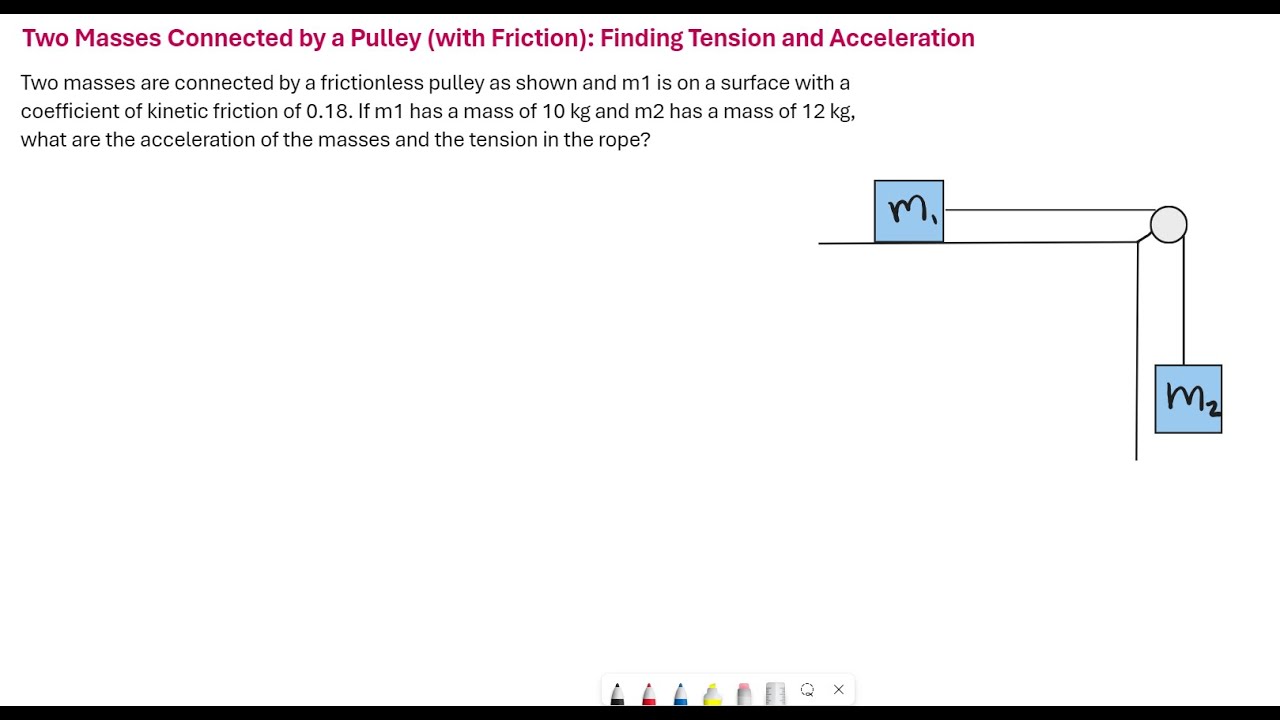
Finding the Tension and Acceleration for a Two Mass Pulley (with Friction)

2015 AP Physics 1 free response 1c
5.0 / 5 (0 votes)
Thanks for rating: