How to Calculate Population Mean (Parameter and Examples) | Statistics

Learn2Stats
12 Feb 202104:24
EducationalLearning
32 Likes 10 Comments

TLDRThe video script discusses the concept of population mean as a parameter, contrasting it with sample mean. It explains that a parameter is a constant, not an approximation, and provides two examples: calculating the average family size for seven families in a neighborhood and the average weight of all residents in a city with 2239 people. The script emphasizes the practicality of understanding population mean for real-world applications.

Takeaways
  • πŸ“ The video discusses the concept of population mean and provides examples to illustrate it.
  • πŸ”’ A parameter, such as the population mean (mu), is a constant that is not an approximation but an exact value.
  • 🏠 The first example given is calculating the average family size of seven families in a neighborhood, which represents a population mean.
  • πŸ‘¨β€πŸ‘©β€πŸ‘§β€πŸ‘¦ To find the population mean, the sum of all values (x) is divided by the number of families (n), resulting in the average family size.
  • πŸ“Š The calculation yields a population mean of 3.43 for the given family size data.
  • πŸŒ† The second example involves finding the average weight (in kilograms) of all 2239 people in a city, another instance of a population mean.
  • πŸ“ˆ The process for calculating the population mean weight involves summing up all individual weights and dividing by the total number of people.
  • πŸ‹οΈ The average weight of the city's population is given as 76.3 kilograms, which is a true parameter, not an approximation.
  • πŸ” The video emphasizes the difference between parameters and statistics, with parameters being true values for the entire population.
  • πŸ“Š The use of tools like Excel is suggested for handling large datasets to calculate population means efficiently.
  • πŸ’‘ The video highlights the practical applications of understanding population means in real-world scenarios.
Q & A

  • What is the main topic of the video?

    -The main topic of the video is to explain the concept of population mean and provide examples of how to calculate it.

  • What is the formula for calculating the population mean?

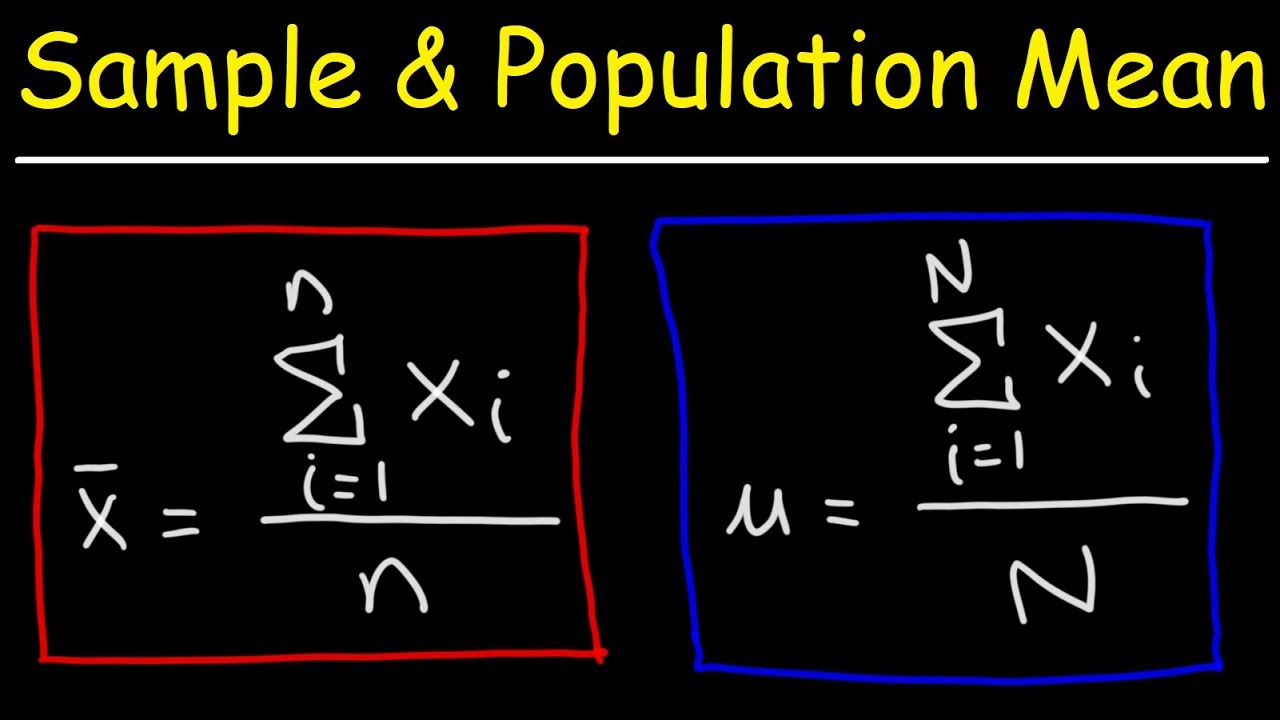
    -The formula for calculating the population mean is the summation of x (i) over n, which equals mu (ΞΌ).

  • What is the difference between a parameter and a sample mean?

    -A parameter is a fixed value that is true for the entire population, whereas a sample mean is an approximation of the population mean based on a subset of the data.

  • How do you calculate the population mean for the family sizes in a neighborhood with seven families?

    -To calculate the population mean for the family sizes, you sum up all the family sizes (7, 1, 3, 2, 4, 3, and 4) and divide by the number of families (7), resulting in an average family size of 3.43.

  • What is the significance of knowing the population mean?

    -Knowing the population mean is significant as it provides an exact value for the entire population, which can be useful for various real-world applications and decision-making processes.

  • How would you calculate the population mean weight of 2239 people in a city?

    -To calculate the population mean weight, you would sum up the weights of all 2239 people and then divide by the total number of people (2239). In the video, this results in an average weight of 76.3 kilograms.

  • Why is it important to distinguish between a parameter and a statistic?

    -It is important to distinguish between a parameter and a statistic because a parameter represents the entire population, while a statistic is an estimate based on a sample. Understanding this difference helps in accurately interpreting and applying statistical results.

  • What tool is commonly used to calculate the population mean for large datasets?

    -For large datasets, tools like Excel or other statistical software are commonly used to calculate the population mean, as manual calculation would be impractical and time-consuming.

  • How does the concept of population mean relate to real-world applications?

    -The concept of population mean relates to real-world applications by providing a way to understand and analyze the average characteristics of a population, which can inform decisions and policies in areas such as public health, urban planning, and social services.

  • What is the role of the population mean in statistical analysis?

    -The population mean plays a crucial role in statistical analysis as it serves as a benchmark or standard for comparing data, calculating other statistics like standard deviation, and making inferences about the population from sample data.

  • Why might one want to calculate the population mean for different scenarios?

    -One might want to calculate the population mean for different scenarios to gain insights into the central tendency of a population, which can help in understanding patterns, making predictions, and informing decisions in various fields such as business, research, and social sciences.

Outlines
00:00
πŸ“Š Understanding Population Mean

This paragraph introduces the concept of the population mean as a parameter that is an exact value, not an approximation. It contrasts this with the sample mean, emphasizing that the population mean represents the entirety of a dataset. The video aims to provide examples of calculating the population mean, using the formula mu = (Ξ£xi) / n, where xi represents individual data points and n is the number of data points. The first example given is calculating the average family size for all seven families in a neighborhood. By summing the family sizes (7, 1, 3, 2, 4, 3, and 4) and dividing by 7, the result is an average family size of 3.43. This calculation demonstrates how the population mean can be determined for a small, complete dataset, which is applicable for understanding local demographics. The second example discusses calculating the average weight of all 2239 people in a city. While the individual weights are not listed, the process is the same: summing the weights and dividing by the total number of people. The result, 76.3 kilograms, is presented as the true average weight, not an estimate, highlighting the reliability of the population mean when the entire population is measured.

Mindmap
Keywords
πŸ’‘Population Mean
The population mean, often denoted by the Greek letter mu (ΞΌ), is the average value of a specific characteristic for an entire population. In the video, it is explained as a parameter that is a true value, not an approximation or guess. It is calculated by summing all the individual values (x) in the population and dividing by the number of individuals (n). For example, the average family size of seven families in a neighborhood is considered a population mean because the entire neighborhood's family sizes are taken into account.
πŸ’‘Parameter
A parameter is a numerical value that describes a characteristic of a population. It is distinct from a statistic in that it represents an actual property of the entire population rather than an estimate based on a sample. In the context of the video, the population mean is a parameter, and it is calculated using the formula Ξ£x_i / n, where n is the number of individuals in the population. The video emphasizes that parameters are factual and do not require estimation or approximation.
πŸ’‘Sample Mean
The sample mean is an estimate of the population mean based on a subset of the population. Unlike the population mean, which includes all members of a population, the sample mean is derived from a limited number of observations. The video contrasts the population mean with the sample mean, highlighting that the latter is an approximation used when it is impractical to collect data from every member of the population.
πŸ’‘Formula
The formula mentioned in the video is the mathematical expression used to calculate the population mean, represented as Ξ£x_i / n. This formula is a fundamental tool in statistics for determining the average of a set of values. The video provides a step-by-step process for applying this formula to real-world data, such as the family sizes in a neighborhood, to arrive at the population mean.
πŸ’‘Family Size
Family size is an example used in the video to illustrate the concept of the population mean. It refers to the number of individuals in a family and is used to demonstrate how to calculate the average family size for all families in a given neighborhood. The video uses the specific family sizes of 7, 1, 3, 2, 4, 3, and 4 to calculate the population mean, which is 3.43, showing how this parameter is determined for a small, defined population.
πŸ’‘Weight
Weight, in the context of the video, refers to the body weight of individuals and is used as an example to explain the calculation of the population mean for a larger group, such as the 2239 people in a city. The video explains that the population mean weight is determined by summing the weights of all individuals and dividing by the total number of people, resulting in an average weight for the entire city.
πŸ’‘Excel
Excel, mentioned in the video, is a widely used spreadsheet application that can be employed to process and analyze data. The video suggests using Excel or similar software to calculate the population mean for large datasets, such as the weights of 2239 people, as it would be impractical to do so manually.
πŸ’‘Statistic
A statistic is a numerical value that is calculated from a sample of a population and is used to estimate population parameters. The video differentiates between statistics and parameters, emphasizing that while statistics are estimates based on samples, parameters are true values that describe the entire population. The population mean, as discussed in the video, is a parameter, not a statistic.
πŸ’‘Data Overload
Data overload refers to the situation where an individual is presented with an excessive amount of data, making it difficult to process or analyze effectively. In the video, the commentator mentions that showing a list of 2239 people's weights would result in data overload and would not be meaningful to the viewer. Instead, the video focuses on the process of summarizing and calculating the population mean without overwhelming the audience with raw data.
πŸ’‘Real World Application
Real world application refers to the practical use of statistical methods and concepts in everyday life. The video emphasizes the importance of understanding the population mean by providing examples such as the average family size in a neighborhood and the average weight of people in a city. These examples illustrate how statistical concepts can be applied to gain insights into real-life situations and make informed decisions.
πŸ’‘Commentator Request
The video was created in response to a commentator's request for more examples of population means. This indicates that the content was tailored to address a specific query from the audience, showcasing the interactive nature of content creation and the importance of engaging with viewers to meet their informational needs.
Highlights

The video discusses the concept of population mean and provides examples for better understanding.

A parameter, such as the population mean (mu), is an exact value, not an approximation.

The formula for population mean is the summation of x(i) over n, equal to mu.

The first example given is calculating the average family size of seven families in a neighborhood.

The population mean is calculated by summing all family sizes and dividing by the number of families.

The example demonstrates how to calculate the average family size as 3.43 people.

The video emphasizes the real-world application of calculating population mean for family sizes.

The second example is about finding the average weight of 2239 people in a city.

For large data sets like 2239 people's weights, software like Excel is used for calculations.

The average weight calculation results in a population mean of 76.3 kilograms.

The video clarifies that the population mean is a true value, not an approximation like a sample mean.

The video also touches on how parameters like population mean can be used to calculate standard deviation.

The content is engaging and educational, encouraging viewers to like, subscribe, and comment with questions.

The video is a response to a commenter's request, showcasing the video creator's interactive approach with the audience.

The video concludes with a call to action for viewers to stay engaged with the content and the community.

Transcripts

Browse More Related Video

Sample Mean and Population Mean - Statistics

Population Mean And Sample Mean (Explanation and Walkthrough Example) |Statistics

6.3.5 Sampling Distributions and Estimators - Biased and Unbiased Estimators

What is an unbiased estimator? Proof sample mean is unbiased and why we divide by n-1 for sample var

Statistics: Sample vs. Population Mean

6.4.4 The Central Limit Theorem - Finite Population Correction Factor

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Population MeanStatistical ConceptsFamily SizesAverage WeightData AnalysisExcel UsageReal-world StatsEducational ContentCommentator RequestNerdy Knowledge