Change of Basis
TLDRThe script explains how to change from one vector basis to another in vector spaces like R2. It starts with the standard basis vectors i and j, and shows how any vector v can be written as a linear combination of those. It then introduces a new basis, u1 and u2, and relates them to the standard basis using a transition matrix U. By setting two expressions for v equal, one in each basis, it shows how to solve for the new coefficients v′. It notes U is made of the new basis vectors as columns. Finally, it explains going between non-standard bases requires using the standard basis as an intermediate step.
Takeaways
- 😀 We can write any vector in R2 as a linear combination of the standard basis vectors i and j
- 😇 By changing basis, we are essentially creating new axes in that vector space
- 🤓 The transition matrix relates the coefficients in one basis to the coefficients in another basis
- 😎 The transition matrix has the new basis vectors as its columns
- 🧐 To get the transition matrix, write the new basis vectors in terms of the standard basis
- 🤔 To relate two non-standard bases, use the standard basis as a stepping stone
- 💡 Taking the inverse of the transition matrix isolates the vector of new coefficients
- 🌟 Plugging in numbers gives the coordinates of a vector in the new basis
- ✨ Change of basis is a type of linear transformation
- 👍 Check comprehension on expressing vectors in different bases
Q & A
What is a basis vector and how can changing basis vectors be useful?
-A basis vector is a vector that, together with other basis vectors, spans a vector space and allows you to represent any vector in that space. Changing between bases can help express a problem in a way that is easier to solve.
If v = (v1, v2) represents a vector in terms of the standard basis vectors i and j, how can you write v as a linear combination of i and j?
-v = v1(i) + v2(j), where v1 and v2 are the coordinates of v in the i, j basis.
When changing from one basis to another for the same vector space, what remains unchanged?
-The actual vectors themselves do not change, only their coordinates in the different bases.
How can you easily obtain the transition matrix between any new basis and the standard basis?
-The transition matrix will have the new basis vectors as its columns.
If U is the transition matrix from the standard basis to a new basis, how can you use U to find the coordinates of a vector v in the new basis?
-Multiply the inverse of U by v, or U^-1 * v. This will give you the coordinates of v in the new basis.
How do you relate two non-standard bases using the standard basis?
-You find the transition matrices from each non-standard basis to the standard basis, set them equal, and solve for one set of coordinates in terms of the other.
Why does order matter when multiplying matrices, unlike when multiplying scalars?
-Matrix multiplication is not commutative, meaning A*B ≠ B*A in general. The order affects the output.
What is a determinant of a matrix and how is it useful when finding an inverse?
-The determinant is a scalar value that characterizes the matrix. To find a matrix inverse, you take its adjugate and divide by the determinant.
How are changes of basis related to linear transformations?
-Changes of basis are a type of linear transformation, which transforms vectors in a vector space while preserving linear combinations.
What information does a transition matrix contain about the new basis vectors?
-The columns of the transition matrix directly represent the new basis vectors in terms of the standard basis.
Outlines
😊 Changing Vector Bases
This paragraph explains the concept of changing bases in a vector space. It starts with the standard basis vectors i and j in R^2. Then it introduces a new basis u1 and u2 and shows through algebra how to write a vector v in terms of the new basis. The resulting equation contains a transition matrix U that relates the vector coefficients between the two bases. The transition matrix columns match the new basis vector components.
😀 Finding New Vector Coordinates
This paragraph shows how to use the transition matrix to easily find the coordinates of a vector in a new basis. By multiplying both sides of the equation by the inverse of the transition matrix U, the new vector coefficients v' can be isolated. An example is provided using a vector v = (2, 3) and converting its coordinates to a new basis defined by u1 and u2.
Mindmap
Keywords
💡Basis
💡Vector Space
💡Linear Combination
💡Coordinates
💡Transition Matrix
💡Change of Basis
💡Inverse Matrix
💡Linear Transformation
💡Matrix Multiplication
💡Stepping Stone
Highlights
Basis vectors allow us to express any vector in a vector space as a linear combination.
By changing basis, we are essentially creating new axes in that vector space.
While changing basis, we’re not actually affecting the vector itself.
The matrix that relates the coefficients in different bases is called the transition matrix.
The columns of the transition matrix are the new basis vectors.
To find the new coefficients, multiply the inverse of the transition matrix by the original vector.
The transition matrix only relates a basis to the standard basis.
Relating two non-standard bases requires using the standard basis as an intermediate step.
Change of basis is a type of linear transformation.
Any vector can be written as a linear combination of basis vectors.
Changing basis creates new coordinate axes in the vector space.
The vector itself does not change when changing basis.
The transition matrix relates coefficient vectors in different bases.
Transition matrix columns are the new basis vector representations.
Use transition matrix inverse to find new coefficient vector.
Transcripts
Browse More Related Video
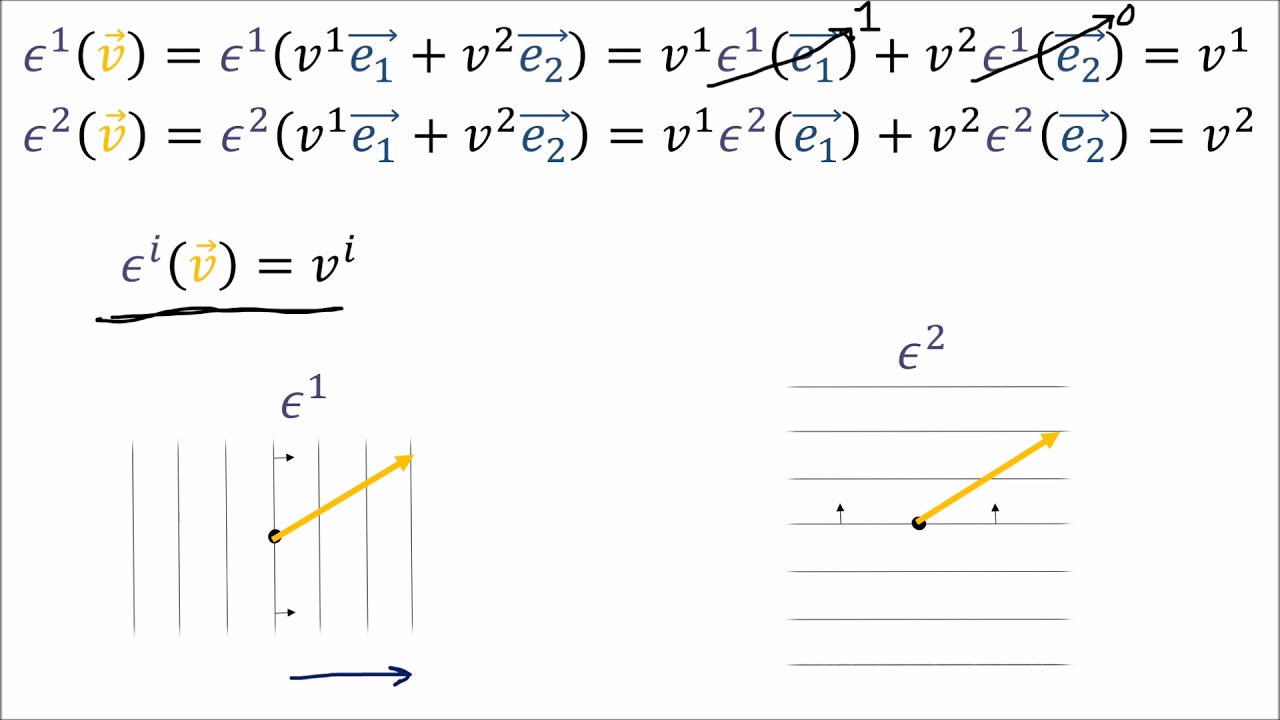
Tensors for Beginners 5: Covector Components (Contains diagram error; see description)
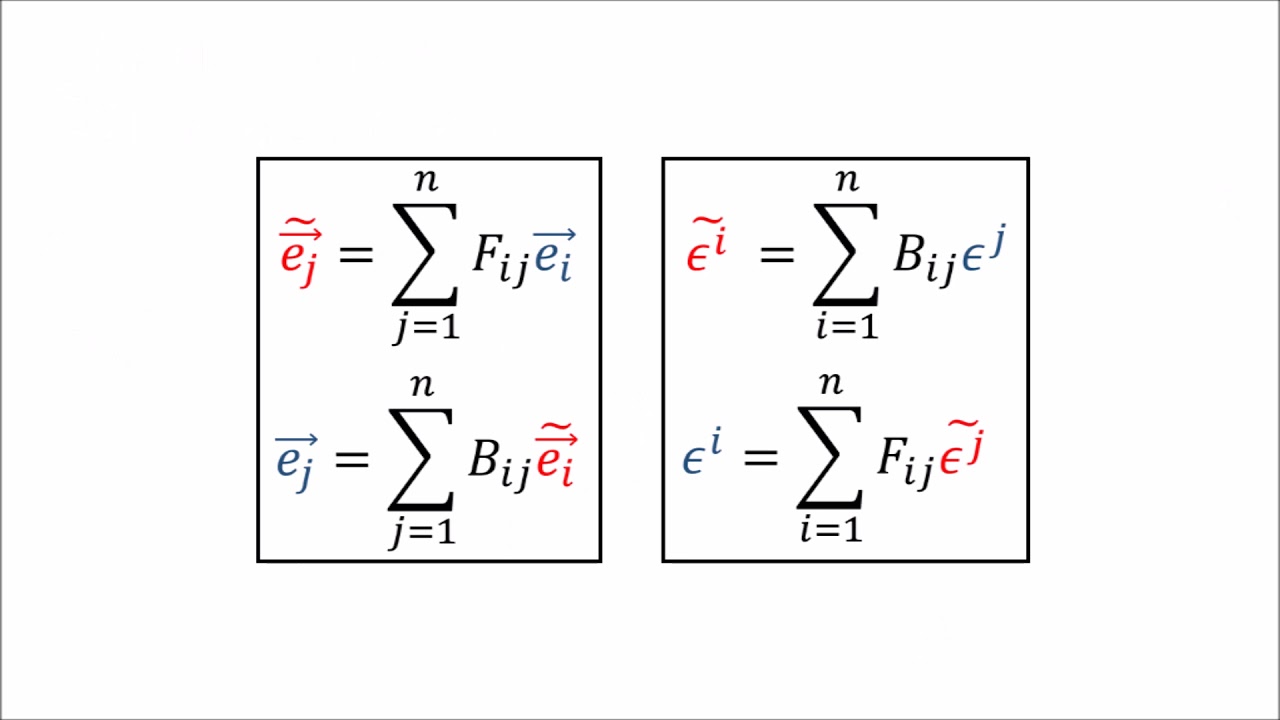
Tensors for Beginners 6: Covector Transformation Rules

Linear combinations, span, and basis vectors | Chapter 2, Essence of linear algebra

Tensors for Beginners 8: Linear Map Transformation Rules
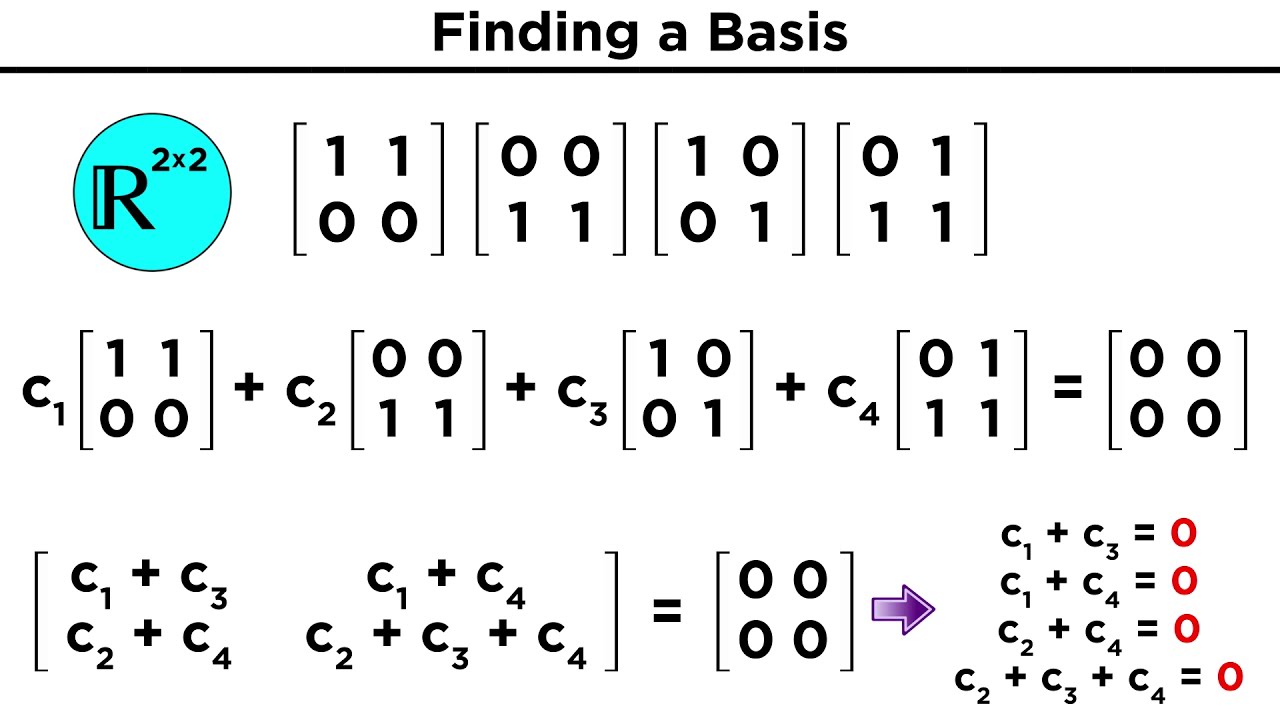
Basis and Dimension

Video 17 - Contravariant Basis
5.0 / 5 (0 votes)
Thanks for rating: