Calculating integral disc around vertical line | AP Calculus AB | Khan Academy
TLDRThe video script presents a step-by-step guide to evaluate the volume of a specific geometric shape, resembling an upside-down gumdrop, using the method of definite integrals. It involves expanding the given expression under the square root, taking the antiderivative of each term, and applying the limits of integration. The process is detailed, showcasing the use of algebraic simplification, u-substitution, and arithmetic to arrive at the final volume, expressed as a fraction of pi. The explanation is clear and methodical, making it accessible for viewers to understand the mathematical concepts involved.
Takeaways
- 📚 The video focuses on evaluating the volume of a specific shape, an upside-down gumdrop-like object, using definite integrals.
- 🧮 The definite integral is set up with respect to the variable y, ranging from -1 to 3.
- 📈 The expression under the square root, y + 1 + 2, is expanded and simplified for further calculations.
- 🔄 The integral involves a combination of basic algebraic manipulation and antiderivative calculations.
- 🤔 The antiderivative of y is y^2/2, while the antiderivative of 4 * sqrt(y + 1) is 8/3 * (y + 1)^(3/2).
- 📝 U-substitution is mentioned as a method for solving the integral, though it is not explicitly used in the video.
- 🌟 The final result includes the constant 5, whose antiderivative is 5y.
- 💻 The evaluation of the integral involves plugging in the upper and lower limits of y (3 and -1) into the antiderivative expressions.
- 🔢 The arithmetic concludes with simplifying the resulting expression, which includes fractions and the number pi.
- 📊 The final volume of the shape is given as 272pi/6, which is further simplified to 136pi/3.
- 🎓 The video serves as an educational resource for viewers interested in learning about definite integrals and their applications in calculating volumes.
Q & A
What was the main topic of the video?
-The main topic of the video was to evaluate the volume of a specific shape, described as an upside-down gumdrop or truffle-looking object, using definite integrals.
What mathematical concept was used to find the volume?
-Definite integrals were used to calculate the volume of the shape.
What was the range of the definite integral?
-The definite integral was set up with y ranging from negative 1 to 3.
What was the expression under the square root in the integral?
-The expression under the square root was y plus 1 plus 2.
How was the expression expanded in the video?
-The expression was expanded by squaring the term under the square root, multiplying by the constant terms, and simplifying the resulting expression.
What was the antiderivative of the expression?
-The antiderivative of the expression involved y squared over 2, 8/3 times y plus 1 to the 3/2 power, and 5y.
How were the antiderivatives evaluated at the bounds of the integral?
-The antiderivatives were evaluated at y equals 3 and y equals negative 1, and then the results were subtracted to find the volume.
What was the final result of the volume calculation?
-The final result of the volume calculation was 136 pi/3, which represents the volume of the upside-down gumdrop-looking shape.
What was the method used to simplify the final fraction?
-The method used to simplify the final fraction involved finding the least common multiple of the denominators and reducing the fraction to its simplest form.
How does this video contribute to understanding definite integrals?
-This video provides a step-by-step walkthrough of evaluating a definite integral to find the volume of a shape, which helps viewers understand the process and application of definite integrals in calculating volumes.
Outlines
📚 Evaluating the Definite Integral for Volume
This paragraph delves into the process of evaluating a definite integral to calculate the volume of a specific shape, an upside-down gumdrop-like figure. The speaker explains the need to expand the given expression, which includes a square root of y plus 1 plus 2, and to perform the integration over the interval from y equals negative 1 to y equals 3. The paragraph outlines the steps to simplify the integrand and find its antiderivative, which involves using techniques like u-substitution and understanding the derivatives and antiderivatives of the functions involved. The goal is to evaluate the entire expression at the bounds of integration and sum up to find the volume, with an emphasis on the mathematical procedures and calculations required.
📈 Simplifying the Resulting Volume Calculation
The second paragraph focuses on simplifying the results obtained from the previous paragraph's calculations. It discusses the process of evaluating the antiderivative at the upper and lower limits of integration and the subsequent arithmetic needed to arrive at the final volume of the shape in question. The speaker guides through the simplification of fractions and the combination of terms to reach a more manageable expression. The paragraph emphasizes the importance of reducing the final result to its simplest form, showcasing the final volume of the upside-down gumdrop-looking object as the product of the comprehensive calculations and simplifications.
Mindmap
Keywords
💡Definite Integral
💡Square Root
💡Antiderivative
💡U Substitution
💡Volume
💡Arithmetic
💡Limits of Integration
💡Integration
💡Differential dy
💡Simplification
💡Evaluation
Highlights
The video focuses on evaluating the volume of a specific shape, an upside-down gumdrop or truffle-looking object, using definite integrals.
The definite integral is set up to calculate the volume, which involves expanding a mathematical expression containing a square root of y plus 1 and 2.
The integral expression is expanded to involve terms like square root of y, 1, 2 times the product of the terms, and 2 squared, which simplifies to involve dy.
The process of simplifying the expression is detailed, highlighting the combination of like terms to prepare for finding the antiderivative.
The antiderivative of the expression is taken, involving concepts like y squared over 2 and 4 times the square root of y plus 1.
The use of u-substitution is mentioned as a method to find the antiderivative, showcasing a common technique in calculus.
The antiderivative of 5 is simply 5y, demonstrating a straightforward aspect of integration.
The evaluation of the antiderivative at specific points (y=3 and y=-1) is explained, which is a crucial step in determining the volume.
The arithmetic to evaluate the expression at y=3 is detailed, including the calculation of 3 squared over 2 and 4 times the square root of 4.
The subtraction of the evaluated expression at y=-1 is described, emphasizing the importance of this step in the calculation.
The final arithmetic simplification is performed, showcasing the process of combining fractions and simplifying the expression.
The least common multiple of the denominators is found to be 6, which is a key step in the simplification process.
The final result is expressed as a product of pi and a fraction, demonstrating the successful application of calculus to find the volume.
The video concludes with the presentation of the volume of the shape, which is the main goal and a significant achievement of the content.
The method used in the video is not only applicable to this specific problem but can also be used as a template for solving similar calculus problems.
The video provides a step-by-step guide that is clear and methodical, making it an excellent resource for learning how to evaluate definite integrals and calculate volumes of complex shapes.
Transcripts
Browse More Related Video

Integration Of Exponential Functions [ Substitution Method ]

Definite integral of rational function | AP Calculus AB | Khan Academy
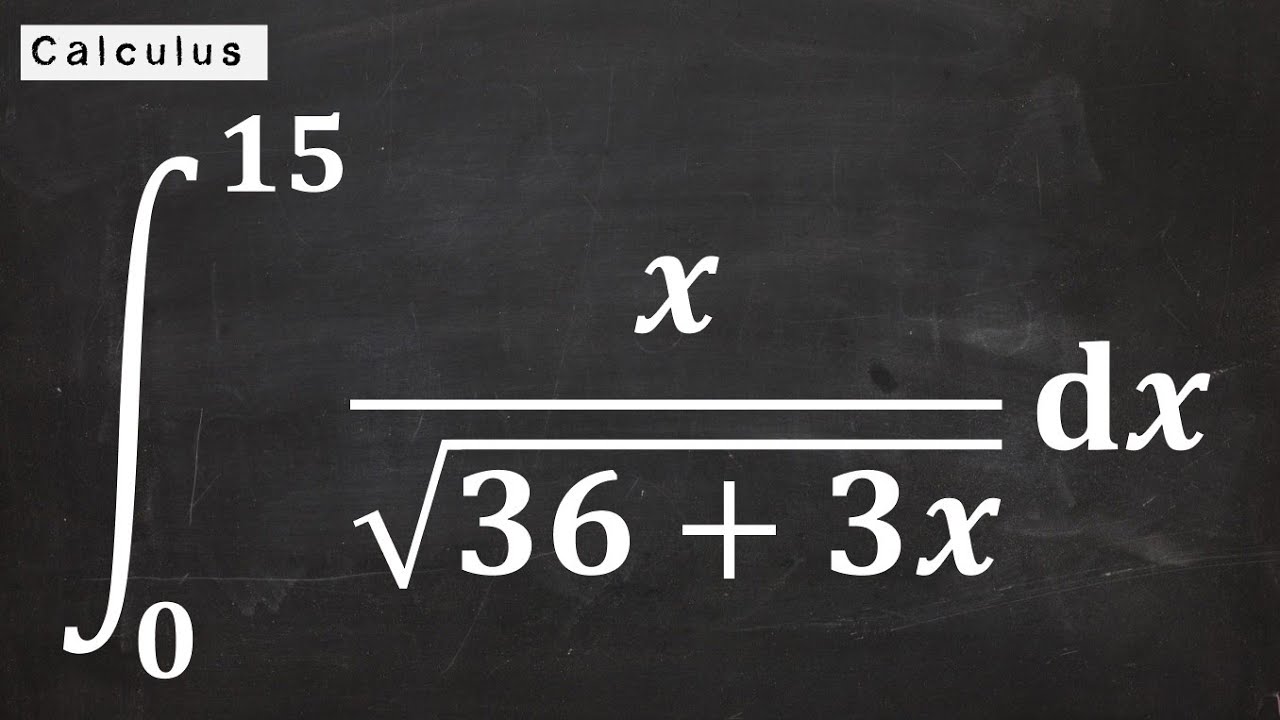
Definite Integral With U-Substitution

Indefinite Integral of Exponential Functions | Calculus

Lesson 16- Integration By Trig Substitution (Calculus 1 Tutor)
Integration Practice I | MIT 18.01SC Single Variable Calculus, Fall 2010
5.0 / 5 (0 votes)
Thanks for rating: