Lesson 16- Integration By Trig Substitution (Calculus 1 Tutor)

Math and Science
5 Mar 201604:00
EducationalLearning
32 Likes 10 Comments

TLDRThe video script discusses the method of integration by trigonometric substitution, a technique used to evaluate integrals that involve expressions under a square root. It emphasizes the importance of recognizing specific expressions, such as the square root of a squared minus x squared, which indicates the need for trigonometric substitution. The script provides a step-by-step guide on how to perform the substitution and introduces relevant trigonometric identities for each case. An example integral is used to illustrate the process, demonstrating how to identify the appropriate substitution and apply the method to solve the integral.

Takeaways
  • 📚 The course section focuses on integration by trigonometric substitution.
  • 🔍 Look for specific expressions to identify when to use trig substitution: √(a^2 - x^2), a^2 + x^2, and x^2 - a^2.
  • 📝 Substitute x with appropriate trigonometric functions: a*sin(θ) for √(a^2 - x^2), a*tan(θ) for a^2 + x^2, and x = a*sec(θ) for x^2 - a^2.
  • 🌟 Relevant trigonometric identities are crucial for the process: 1 - sin^2 = cos^2, 1 + tan^2 = sec^2, and sec^2 - 1 = tan^2.
  • 🧠 Understand that the specific form of the integral guides the choice of substitution and the relevant trig identity.
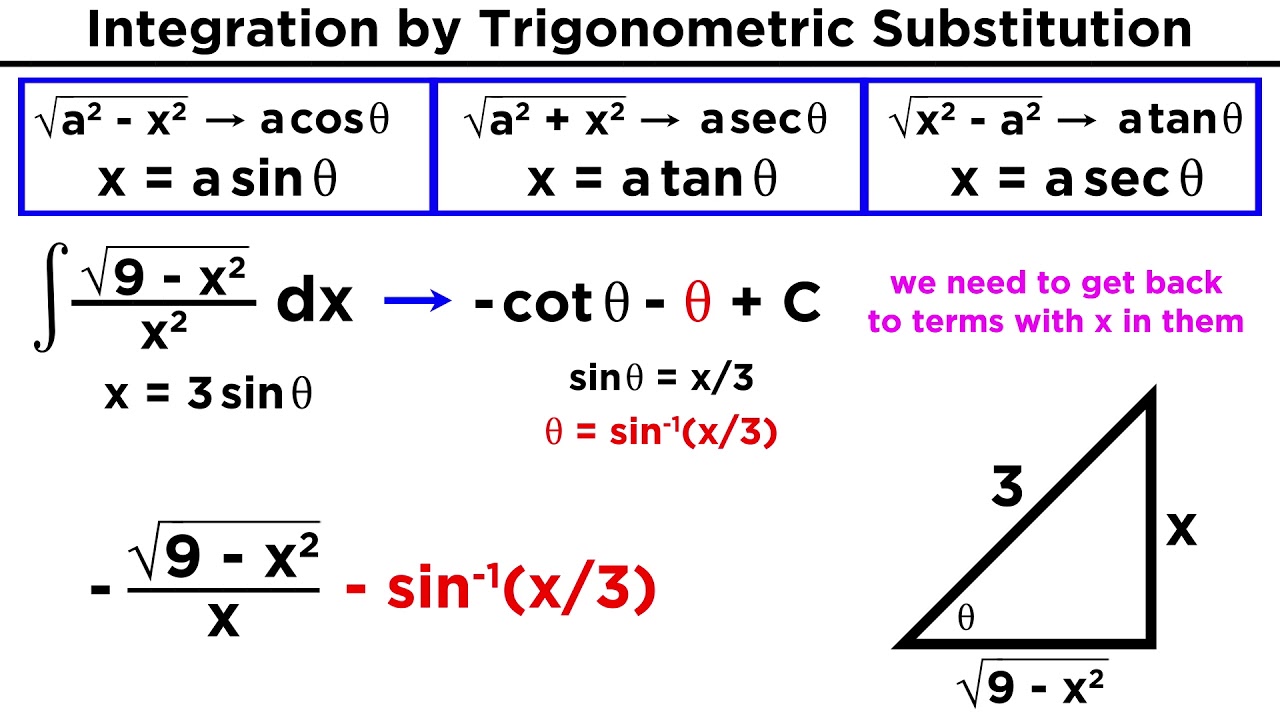
  • 📑 For the example integral ∫√(9 - x^2)/x^2 dx, recognize that it fits the pattern of √(a^2 - x^2) with a = 3.
  • 👉 Perform the substitution: x = 3*sin(θ) and dx = 3*cos(θ)dθ.
  • 📈 After substitution, the integral simplifies to ∫3/(3*sin(θ)^2) * 3*cos(θ)dθ.
  • 🔄 The process involves replacing the original variables with the new trigonometric expressions and adjusting the differential accordingly.
  • 📊 This method can be applied to a variety of integrals that fit the trigonometric substitution pattern.
  • 🎯 Practice is essential to become proficient with these techniques, as the problems can become quite complex.
Q & A

  • What is the main topic of this section of the course?

    -The main topic of this section is integration by trigonometric substitution.

  • What type of expressions should you be on the lookout for when using integration by trig substitution?

    -You should be on the lookout for expressions like the square root of a squared minus x squared, a squared plus x squared, and x squared minus a squared.

  • What is the significance of the expression √(a^2 - x^2) in trigonometric substitution?

    -The expression √(a^2 - x^2) indicates that you should use trigonometric substitution and substitute x with a times the sine of theta (x = a * sin(θ)).

  • How do you handle the expression a^2 + x^2 in trigonometric substitution?

    -For the expression a^2 + x^2, you substitute x with a times the tangent of theta (x = a * tan(θ)).

  • What substitution is used for the expression x^2 - a^2?

    -For the expression x^2 - a^2, you substitute x with a times the secant of theta (x = a * sec(θ)).

  • What is the relevant identity for the first case of trigonometric substitution (√(a^2 - x^2))?

    -The relevant identity for this case is 1 - sin^2 = cos^2.

  • What identity is useful for the second case of trigonometric substitution (a^2 + x^2)?

    -The useful identity for this case is 1 + tan^2 = sec^2.

  • How does the identity for the third case of trigonometric substitution (x^2 - a^2) relate to the others?

    -The identity for the third case is sec^2 - 1 = tan^2, which is essentially the same as the second case's identity but for a different expression.

  • How do you identify the value of 'a' in the expression √(9 - x^2)?

    -In the expression √(9 - x^2), 'a' is equal to 3, as the expression can be written as √(3^2 - x^2).

  • What is the derivative of x = a * sin(θ) with respect to θ?

    -The derivative of x = a * sin(θ) with respect to θ is dx/dθ = a * cos(θ).

  • What is the final step in setting up the integral ∫√(9 - x^2)/x^2 dx after substitution?

    -After substitution, the final step is to replace dx with 3cos(θ)dθ, which is the derivative of the trigonometric substitution in terms of θ.

Outlines
00:00
📚 Introduction to Integration by Trig Substitution

This paragraph introduces the concept of integration by trigonometric substitution, a method used to solve integrals that involve expressions under a square root. The instructor emphasizes the importance of recognizing specific expressions, such as the square root of a squared minus x squared, a squared plus x squared, and x squared minus a squared, which indicate the need for trig substitution. The paragraph also outlines the substitutions for these expressions: x as a times the sine of theta, a times the tangent of theta, and a times the secant of theta, respectively. Additionally, it introduces relevant trigonometric identities for each case, which are crucial for the integration process.

Mindmap
Keywords
💡Integration by Trig Substitution
Integration by Trig Substitution is a method used in calculus to evaluate integrals that involve radical expressions, particularly those that can be related to trigonometric functions. It simplifies the process by transforming the integral into a more manageable form through substitution. In the video, the professor introduces this technique and provides specific expressions to look out for, such as the square root of a squared minus x squared, which indicates the use of trig substitution.
💡Square Root
A square root is a mathematical operation that finds the value which, when squared, equals the given number. In the context of the video, square roots often appear in integrals that require trigonometric substitution. The professor emphasizes looking for expressions under a square root, such as the square root of a squared minus x squared, which is a key indicator for using this method.
💡Trigonometric Functions
Trigonometric functions, such as sine, cosine, and tangent, are mathematical functions that relate angles to real numbers. They are widely used in solving problems involving periodic phenomena and right triangles. In the video, these functions are crucial for the substitution process, where the variable x is expressed in terms of trigonometric functions to simplify the integral.
💡Substitution
Substitution is a mathematical technique used to simplify expressions or equations by replacing one or more variables with other expressions. In the context of the video, substitution is the core of the trig substitution method, where the variable x is replaced with a trigonometric expression to transform the integral into a form that can be more easily evaluated.
💡Derivative
The derivative is a fundamental concept in calculus that represents the rate of change of a function with respect to its variable. In the process of integration by trig substitution, derivatives play a crucial role in transforming the original integral into a new form. The professor mentions taking the derivative of the substitution expression, such as the derivative of x with respect to theta, to facilitate the integration process.
💡Relevant Identities
Relevant identities are mathematical equations that relate different trigonometric functions and are used to simplify expressions. In the video, the professor introduces specific identities that correspond to the type of trig substitution being used, such as 1 minus sine squared equals cosine squared, which is essential for simplifying the integral after the substitution has been made.
💡Sine Function
The sine function is one of the fundamental trigonometric functions that relates the angle of a right triangle to the ratio of the length of the opposite side to the hypotenuse. In the video, the sine function is used in the substitution process, where x is expressed as a times the sine of theta, allowing for the simplification of the integral through trigonometric manipulation.
💡Tangent Function
The tangent function is another trigonometric function that defines the ratio of the opposite side to the adjacent side in a right triangle. In the context of the video, tangent is used in the substitution process for certain integrals, such as when the integral involves the expression a squared plus x squared, where x is substituted with a times the tangent of theta.
💡Secant Function
The secant function is the reciprocal of the cosine function and is used in trigonometry to relate the angle of a right triangle to the ratio of the hypotenuse to the adjacent side. In the video, the secant function is involved in the substitution for integrals where the expression x squared minus a squared is present, with x being substituted as a times the secant of theta.
💡Trig Substitution Patterns
Trig Substitution Patterns are specific expressions that, when identified in an integral, indicate which trigonometric substitution to use. These patterns are crucial for applying the method of trig substitution correctly. The video script outlines three key patterns: square root of a squared minus x squared, a squared plus x squared, and x squared minus a squared, each corresponding to different substitution methods.
💡Integral
An integral is a mathematical concept used to calculate the area under a curve or the accumulation of a quantity over a given interval. In the video, integrals are the focus of the lesson, and the professor is teaching how to evaluate them using the method of trigonometric substitution for certain types of integrals that involve radical expressions.
Highlights

Integration by trig substitution is the focus of this course section.

The first expression to look for is the square root of a squared minus x squared.

For the expression a squared minus x squared, substitute x with a times the sine of theta.

When encountering a squared plus x squared, use a times tangent theta for substitution.

For x squared minus a squared, the substitution involves x equals a times the secant of theta.

The relevant identity for the first case is one minus sine squared equals cosine squared.

The identity for the second case is one plus tangent squared equals secant squared.

The third case uses the identity secant squared minus 1 equals tangent squared.

An example integral is provided: the square root of nine minus x squared over x squared.

The integral can be rewritten as the square root of 3 squared minus x squared over x squared DX.

The substitution in this example is x equals a sine theta, with a equals 3.

Derivative of x with respect to theta is three times the cosine of theta.

DX equals 3 cosine theta d theta after the substitution and derivative calculation.

The process involves writing down the expression, taking its derivative, and then performing substitution.

The integral kind takes the form of a squared minus x squared, indicating the substitution needed.

The method is applicable to integrals that contain expressions similar in form to the ones discussed.

Working through additional problems is encouraged to gain proficiency in this technique.

Transcripts

Browse More Related Video

Integration By Trigonometric Substitution

AP Calculus AB Crash Course Day 2 - Integration

Trig Substitution... How? (NancyPi)

_-substitution: defining _ | AP Calculus AB | Khan Academy

Trigonometric Substitution

Integrals: Trig Substitution 3 (long problem)

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
TrigSubstitutionIntegrationTechniqueMathematicsAdvancedCalculusEducationOnlineLearningMathTutorialsTrigonometryIntegralsAcademia