Integration Practice I | MIT 18.01SC Single Variable Calculus, Fall 2010
TLDRThis video script is an educational walkthrough on finding integrals and antiderivatives using various mathematical techniques. The presenter begins by introducing the topic and setting up two problems: one involves finding a specific integral of a fraction, and the other is finding an antiderivative of a given function. For the first problem, the method of partial fraction decomposition is used, which simplifies the integral into two separate integrals. The presenter then employs substitution to solve one of the integrals and directly applies the natural logarithm for the other. The second problem involves a trigonometric substitution to simplify the integral, which is then solved using the properties of secant and tangent functions. The video concludes with the presenter providing the final antiderivative in terms of x. The script is a comprehensive guide, demonstrating step-by-step problem-solving in calculus, and is particularly useful for students or anyone looking to understand the application of integration techniques.
Takeaways
- 📚 The video focuses on finding the best technique for calculating integrals or antiderivatives.
- 🔍 The first problem involves finding the integral from -1 to 0 of a given fraction, which requires partial fraction decomposition.
- 🧩 To ensure partial fraction decomposition is applicable, the numerator's degree must be less than the denominator's degree.
- 🤔 The degree check confirms no need for long division, allowing the problem to proceed directly to decomposition.
- 📈 After decomposition, the first integral involves a substitution strategy, recognizing the derivative of (x^2 + 1) as (2x).
- 📉 The second integral from decomposition simplifies to a natural logarithm function, (ln|x - 1|).
- 🌟 The final answer for the first problem is (-4ln(2)) after evaluating the integrals at the bounds.
- 🔁 The second problem involves finding an antiderivative of a function with a domain where the expression under the square root is positive.
- 🧮 Completing the square in the second problem makes it conducive to a trigonometric substitution, specifically using cosine.
- 📐 The trigonometric substitution (cos(theta) = x + 1) is chosen for its simplicity and the ease of dealing with secants over cosecants.
- 🔙 Converting back from trigonometric to Cartesian coordinates involves finding the values of secant and tangent in terms of (x) using the Pythagorean theorem.
- ✅ The antiderivative of the function in terms of (x) is found by substituting the values of secant and tangent back into the natural logarithm expression.
Q & A
What is the main topic of the video?
-The main topic of the video is to establish the best technique for finding an integral or an antiderivative.
What is the first integral problem presented in the video?
-The first integral problem is to find the integral from minus 1 to 0 of the fraction (5x^2 - 2x + 3) / (x^2 + 1)(x - 1).
What technique is suggested for solving the first integral problem?
-Partial fraction decomposition is suggested for solving the first integral problem.
What is the condition checked before using partial fractions?
-The condition checked before using partial fractions is to ensure that the degree of the numerator is smaller than the degree of the denominator.
What is the second problem presented in the video?
-The second problem is to find an antiderivative of the function 1 / (x + 1) * sqrt(-x^2 - 2x).
What is the domain condition for the second problem?
-The domain condition for the second problem is that the expression inside the square root must be positive.
What strategy is used to solve the second integral problem?
-The strategy used to solve the second integral problem is a trigonometric substitution, specifically using cosine.
What trigonometric substitution is used in the second problem?
-The trigonometric substitution used is cosine theta equals x plus 1.
How is the integral of secant in terms of theta represented?
-The integral of secant in terms of theta is represented as the negative natural log of the absolute value of secant theta plus tangent theta.
What is the final answer for the first integral problem?
-The final answer for the first integral problem is negative 4 times the natural log of 2.
How is the relationship between secant and tangent used to finish the second problem?
-The relationship between secant and tangent is used to substitute back into the antiderivative in terms of x after performing the trigonometric substitution.
What is the final expression for the antiderivative of the second problem in terms of x?
-The final expression for the antiderivative of the second problem in terms of x is the negative natural log of the absolute value of (1 / (x + 1)) + sqrt(1 - (x + 1)^2) plus a constant c.
Outlines
📚 Introduction to Finding Integrals and Antiderivatives
The video begins with an introduction to the topic of finding integrals and antiderivatives. The presenter outlines the two problems that will be addressed: calculating the integral from -1 to 0 of a given fraction, and finding the antiderivative of a function involving a square root. The focus is on selecting the appropriate strategy for each problem and working through the solution. The presenter emphasizes the importance of checking the degree of the numerator relative to the denominator when using partial fraction decomposition and suggests that the first problem will yield a numerical value.
🧩 Partial Fraction Decomposition and Substitution Techniques
The presenter moves on to solve the first problem using partial fraction decomposition, providing the resulting integrals without showing the decomposition process. The integrals involve terms that can be simplified through substitution and direct integration. The strategy involves recognizing the derivative of the denominator in the numerator, which leads to a natural logarithm. The presenter then evaluates the integral at the given bounds, resulting in an answer involving the natural logarithm of 2.
📐 Trigonometric Substitution for Complex Integrals
For the second problem, the presenter rewrites the integral and suggests using trigonometric substitution to simplify the expression under the square root. The goal is to complete the square and transform the integral into a form that allows for easier integration. The presenter chooses a cosine substitution due to personal preference and familiarity with secants. The substitution leads to an expression involving secant, which is then integrated to yield a natural logarithm involving secant and tangent. Finally, the presenter returns to the original x variable by using the relationships established by the trigonometric substitution, completing the antiderivative in terms of x.
Mindmap
Keywords
💡Antiderivative
💡Partial Fraction Decomposition
💡Substitution
💡Natural Logarithm
💡Trigonometric Substitution
💡Completing the Square
💡Domain
💡Absolute Value
💡Derivative
💡Integration
💡Secant and Tangent
Highlights
The video focuses on establishing the best technique for finding an integral or antiderivative.
Two integral problems are worked on in the video.
For the first problem, partial fraction decomposition is the suggested method.
The degree of the numerator should be smaller than the degree of the denominator for partial fractions.
The integral is evaluated from -1 to 0 for the first problem.
For the second problem, the goal is to find an antiderivative, not an exact value.
The function in the second problem is defined as long as the value inside the square root is positive.
A trigonometric substitution is used for the second problem.
Completing the square on the quadratic term inside the square root is a key step in the second problem.
The cosine substitution cos(θ) = x + 1 is chosen for the second problem.
The antiderivative of secant in terms of θ is derived using the relationship secant = 1/cosine.
The final antiderivative is expressed in terms of x by substituting back the values of secant and tangent.
The video provides a step-by-step solution to both integral problems.
The video emphasizes the importance of choosing the right strategy for each problem.
The video demonstrates the use of substitution and partial fraction decomposition techniques in solving integrals.
The video explains the process of evaluating definite integrals by plugging in the limits of integration.
The video shows how to simplify the integral using trigonometric identities after the substitution.
The video reminds viewers of the antiderivative formula for secant in terms of secant and tangent.
The video concludes with a summary of the key steps and strategies used in solving the two integral problems.
Transcripts
Browse More Related Video

AP Calculus AB Crash Course Day 2 - Integration
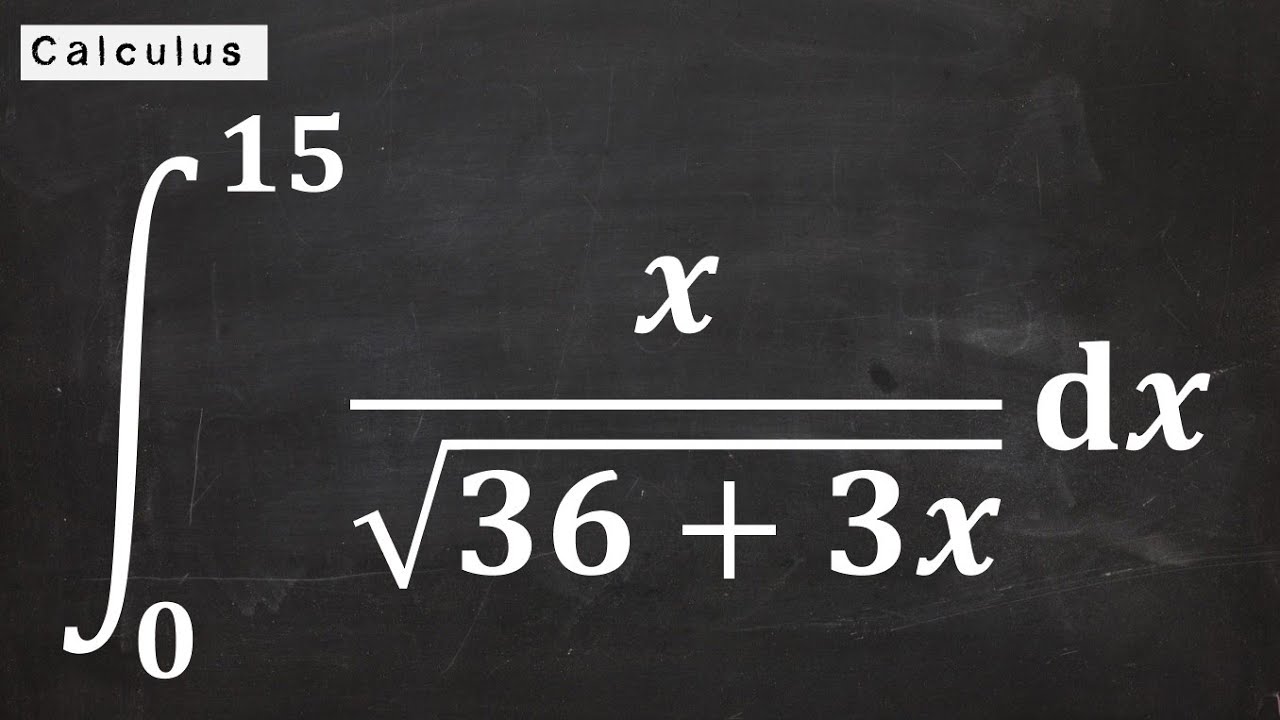
Definite Integral With U-Substitution

Integration Practice IV | MIT 18.01SC Single Variable Calculus, Fall 2010

Integration Of Exponential Functions [ Substitution Method ]

Definite Integrals from Graphs (Part 2 of 3) - U-Substitution

Back Substitution - When a u-sub doesn't match cleanly!
5.0 / 5 (0 votes)
Thanks for rating: