2011 Calculus AB free response #4b | AP Calculus AB | Khan Academy

Khan Academy
8 Sept 201113:15
EducationalLearning
32 Likes 10 Comments

TLDRThe video script discusses the process of determining the x-coordinate of the absolute maximum of a function g on a given interval. The explanation begins with a general overview of how to find the absolute maximum on an interval, considering various scenarios where the maximum could occur. The function g is derived from another function f, and the video demonstrates evaluating g at the interval's endpoints and any critical points within the interval. By analyzing the derivative of g and solving for when it equals zero, the critical point at x=5/2 is identified where g reaches its absolute maximum on the interval from -4 to 3.

Takeaways
  • πŸ“ˆ The task is to find the x-coordinate where a function g has an absolute maximum on a given interval [-4, 3].
  • πŸ” To solve this, one must evaluate g at the endpoints and any critical points within the interval.
  • πŸ€” The absolute maximum could occur at the start, end, or at a critical point within the interval.
  • 🧐 The function g is derived from another function f, and its critical points may not always be points of differentiability.
  • πŸ“Œ The process involves evaluating g at -4 and 3, and checking for critical points in between.
  • πŸ“Š For g(-4), the value is negative, calculated using the integral of the function f over the interval [0, -4].
  • πŸ“ˆ At the endpoint g(3), the function value is positive, with the integral from 0 to 3 cancelling out due to symmetry.
  • 🌟 The derivative of g, g'(x), is found by differentiating the expression of g and checking for points where g'(x) = 0.
  • πŸ”’ The function f is linear in the interval of interest, with a slope of -2, leading to the equation -2x + 3 = -2.
  • 🎯 The x-coordinate of the critical point is found to be 5/2 by solving the equation for x.
  • πŸ₯‡ The absolute maximum of g on the interval [-4, 3] occurs at x = 5/2, with a value of 6.25 (or 5/4).
Q & A

  • What is the main topic of the video script?

    -The main topic of the video script is to determine the x-coordinate of the point at which the function g has an absolute maximum on the interval from negative 4 to 3.

  • How does the speaker initially approach the problem?

    -The speaker initially approaches the problem by thinking in general terms about a function over an interval where it could have an absolute maximum, and then draws axes to visualize the situation.

  • What are the different scenarios the speaker considers for the function's absolute maximum?

    -The speaker considers three different scenarios for the function's absolute maximum: the maximum occurring at the beginning of the interval, at the end of the interval, or at a critical point within the interval.

  • How does the speaker evaluate the function g at the endpoints of the interval?

    -The speaker evaluates the function g at the endpoints by calculating g(-4) and g(3) using the given function definition and integration.

  • What is the result of evaluating g at the starting point (-4)?

    -The result of evaluating g at the starting point (-4) is a negative number, specifically -8 - 2Ο€.

  • What is the result of evaluating g at the end point (3)?

    -The result of evaluating g at the end point (3) is a positive value, which is 6.

  • How does the speaker determine the critical points within the interval?

    -The speaker determines the critical points within the interval by finding where the derivative of g, g'(x), is equal to 0 or by identifying points where the function is not differentiable.

  • What is the equation of the function f(x) that the speaker identifies as being relevant to the problem?

    -The equation of the function f(x) that the speaker identifies is y = -2x + 3, which is relevant for determining the critical points of g(x).

  • What x-value satisfies f(x) = -2?

    -The x-value that satisfies f(x) = -2 is x = 5/2.

  • What is the final answer for the x-coordinate of the absolute maximum of g on the interval?

    -The final answer for the x-coordinate of the absolute maximum of g on the interval is x = 5/2.

  • How does the speaker confirm that the critical point at x = 5/2 is indeed the point of absolute maximum?

    -The speaker confirms that the critical point at x = 5/2 is the point of absolute maximum by evaluating g(x) at this point and comparing it with the values of g at the endpoints, finding that g(5/2) > g(-4) and g(5/2) > g(3).

Outlines
00:00
πŸ“Š Determining Absolute Maximum and Critical Points

This paragraph introduces the problem of finding the x-coordinate of the absolute maximum of a function g on a given interval, and sets the stage for the analysis. The speaker begins by discussing the general concept of absolute maximums on an interval and illustrates this with a graphical representation of different possible functions. The focus is on evaluating the function g at the interval's endpoints and checking for critical points within the interval. The speaker calculates g(-4) and explains the process of evaluating the integral part of the function, which involves understanding the area under the curve and accounting for negative areas. The result is g(-4) = -8 - 2Ο€, indicating a negative value.

05:03
πŸ“ˆ Evaluating Endpoints and Differentiability

In this paragraph, the speaker continues the analysis by evaluating g at the other endpoint of the interval, x=3. The calculation leads to g(3) = 6, which is a positive value, contrasting with the negative value found at the starting point. The speaker then discusses the differentiability of g and uses the fundamental theorem of calculus to find its derivative, g'(x) = 2 + f(x). It is determined that g is differentiable throughout the interval, and the next step is to find any critical points by setting the derivative equal to zero. The speaker visually identifies a point where f(x) = -2 and calculates the x-value to be 5/2.

10:04
πŸ”’ Critical Point Evaluation and Absolute Maximum Determination

The final paragraph focuses on evaluating the function g at the critical point x=5/2, which is suspected to be a potential maximum due to the derivative being zero at this point. The speaker calculates g(5/2) using the integral of the function's derivative and the value of the function at the critical point. After solving the integral and performing the evaluation, the result is g(5/2) = 6.25, which is higher than the values of g at both endpoints. This confirms that the x-coordinate of the absolute maximum of g on the interval is indeed 5/2, providing a conclusion to the analysis.

Mindmap
Keywords
πŸ’‘Absolute Maximum
The absolute maximum of a function on a given interval is the highest value that the function attains on that interval. In the context of the video, the absolute maximum refers to the highest value of function g within the interval from negative 4 to 3. The video aims to determine the x-coordinate where this absolute maximum occurs.
πŸ’‘Interval
In mathematics, an interval refers to a continuous set of numbers ranging between two values. In the video, the interval is the specified range from negative 4 to 3, within which the function g is being analyzed for its maximum value.
πŸ’‘Critical Point
A critical point of a function is a point in the domain of the function where the derivative is either zero or undefined. In the context of the video, critical points are considered as potential candidates for the location of the absolute maximum of the function g.
πŸ’‘Derivative
The derivative of a function at a certain point is the rate of change or the slope of the function at that point. In the video, the derivative of the function g is used to find critical points and to determine the behavior of the function, such as whether it is increasing or decreasing at certain points within the interval.
πŸ’‘Integration
Integration is the process of calculating the area under a curve or the antiderivative of a function. In the video, integration is used to find the area under the curve of function f, which contributes to the calculation of the function g at different points.
πŸ’‘Slope
Slope refers to the measure of the steepness of a line, or in the context of a function, how quickly the function value changes with respect to its independent variable. In the video, the slope of a line representing part of function f is used to determine the x-value where the function equals negative 2.
πŸ’‘Antiderivative
The antiderivative, also known as the indefinite integral, is a function that represents the area under the curve of a given function. In the video, the antiderivative is used to evaluate the integral from 0 to 5/2, which is part of the process to find the value of g at the critical point.
πŸ’‘Area
In the context of the video, area refers to the region enclosed under the curve of a function. The area is used to evaluate the integrals which contribute to finding the values of the function g at different points.
πŸ’‘Differentiable
A function is said to be differentiable at a point if it has a derivative at that point, meaning the function is smooth and its graph does not have any sharp corners, vertical tangents, or breaks. In the video, it is determined that function g is differentiable throughout the interval, which means it is smooth and its derivative can be calculated at any point within the interval.
πŸ’‘Endpoint
In the context of the video, endpoints refer to the starting and ending points of the interval being considered, which are -4 and 3, respectively. Endpoints are important because they are potential locations where the function might reach its maximum or minimum values.
πŸ’‘Global Maximum
A global maximum is the highest value that a function attains over its entire domain. In the video, the focus is on finding the global maximum of the function g within a specific interval, which is from negative 4 to 3.
Highlights

The problem involves finding the x-coordinate where a function g has an absolute maximum on a given interval.

The interval in question is from negative 4 to 3.

The function g is derived from another function f.

The absolute maximum of a function can occur at the beginning, end, or a critical point within the interval.

To find the absolute maximum, evaluate g at the endpoints and any critical points within the interval.

The evaluation of g at negative 4 results in a negative value, indicating it is not the absolute maximum.

The evaluation of g at 3 yields a positive value, suggesting it could be the absolute maximum.

The derivative of g is calculated to find critical points.

It is determined that g is differentiable over the entire interval, which simplifies the search for critical points.

Setting the derivative equal to zero leads to finding the x-value where f(x) is negative 2.

The x-value of 5/2 is found where f(x) equals negative 2.

The evaluation of g at the critical point 5/2 results in a value higher than the endpoints, indicating it is the absolute maximum.

The process involves visual analysis and the use of calculus principles, such as the fundamental theorem of calculus.

The problem-solving approach combines algebraic manipulation with geometric interpretation.

The solution requires a combination of evaluating integrals and understanding the behavior of the function.

The final answer identifies the x-coordinate of the absolute maximum as 5/2.

Transcripts

Browse More Related Video

Absolute Maximum and Minimum Values - Finding absolute MAX & MIN of Functions - Calculus

2022 AP Calculus AB BC Free Response #3

2016 AP Calculus AB Free Response #3

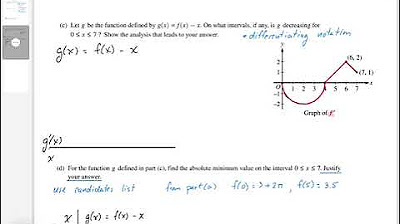
AP CALCULUS AB 2022 Exam Full Solution FRQ#3(c,d)

Finding Absolute Extrema (Max/Min) on a Closed Interval [a, b]

Justification with the intermediate value theorem: equation | AP Calculus AB | Khan Academy

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
MathematicsCalculusFunction AnalysisDerivativesIntegralsAbsolute MaximumCritical PointsInterval AnalysisVisual RepresentationSlope Calculation