Composite Functions Domain Fractions & Square Roots / Radicals - Inverse Functions & Graphs
TLDRThis video script delves into the concept of composite functions, explaining how to find them, determine their domain, and use them to test for inverse functions. It provides step-by-step examples, including replacing variables and evaluating domain restrictions. The script also covers how to graphically confirm if two functions are inverses by reflecting their graphs over the line y=x. The process of finding inverse functions is detailed, emphasizing the importance of switching x and y and solving for the new y. The examples given range from basic polynomials to radicals and cubic functions, demonstrating the versatility of the methods discussed.
Takeaways
- 📚 Composite functions are formed by inserting one function inside another, with the outer function acting on the inner function's output.
- 🔍 To find the composite function f(g(x)), replace every instance of 'x' in the outer function 'f' with the inner function 'g(x)'.
- 🌟 The domain of a composite function is determined by the input function's domain, not the output function's domain.
- ⚠️ When dealing with fractions, the denominator cannot be zero, which may restrict the domain of the composite function.
- 📈 Interval notation is used to represent the domain of a function on a number line, using parentheses for excluded values and brackets for included values.
- 🔄 To find the inverse function, replace 'f(x)' with 'y', switch 'x' and 'y', and solve for 'y'.
- 🖼️ The graphical relationship between a function and its inverse is that they are reflections of each other across the line y=x.
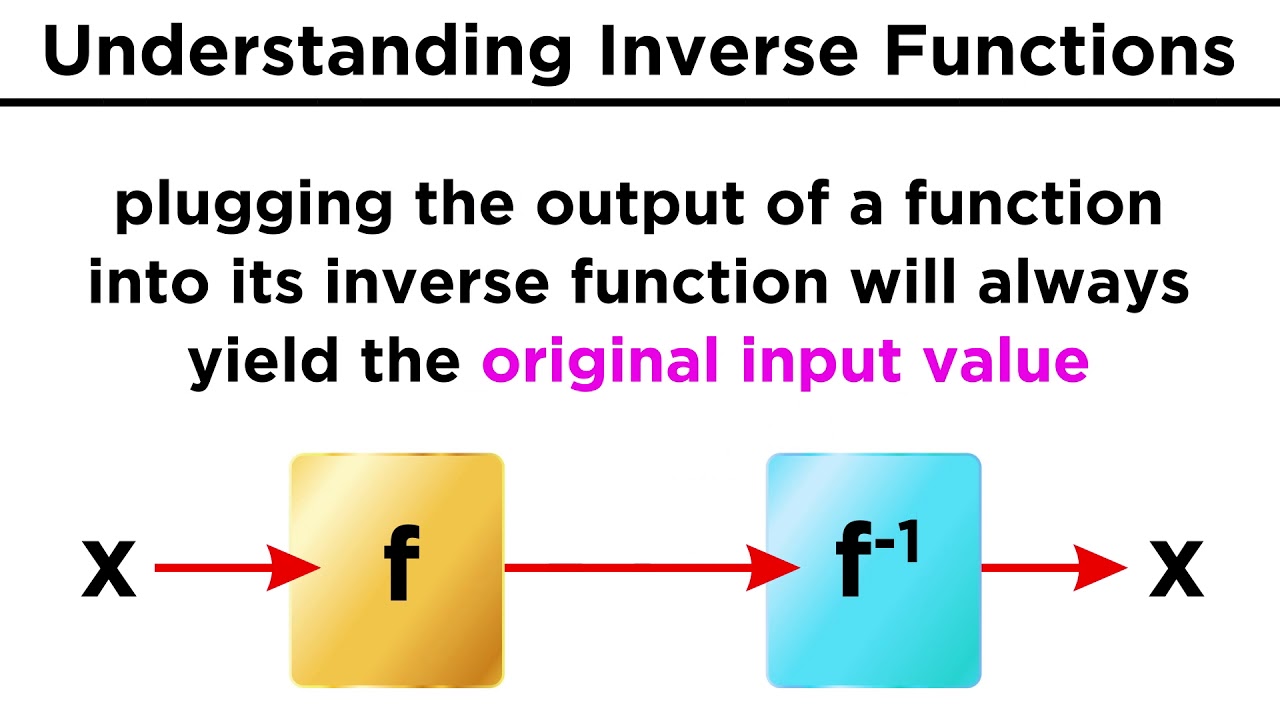
- 🧠 To prove if two functions are inverses, compute the composite functions f(f^(-1)(x)) and g(g^(-1)(x)), and show that both equal 'x'.
- 🛠️ When working with radical functions, the radicand (the expression under the root) must be non-negative for even roots, and can be any real number for odd roots.
- 📊 The domain of a function involving radicals can be found by setting the radicand greater than or equal to zero and solving for 'x'.
- 🔧 To find the domain of a composite function involving multiple restrictions, identify the critical points and test values on a number line.
Q & A
What is a composite function?
-A composite function is a function that is formed by embedding one function inside another. It is denoted as (f ∘ g)(x) or f(g(x)), where f is the outer function and g is the inner function.
How do you find the composite function f(g(x))?
-To find the composite function f(g(x)), you replace the variable in the function f(x) with the expression for g(x). Essentially, you treat g(x) as the input to the function f.
What is the domain of a composite function?
-The domain of a composite function is the set of all possible input values for the inner function g(x) that result in valid outputs for the outer function f(x). It is restricted by the domain of the input function, not the output function.
How do you represent the domain of a composite function using interval notation?
-The domain of a composite function can be represented using interval notation by plotting the solution on a number line and indicating with open or closed circles the points that are included or excluded from the domain.
What is the inverse function and how do you find it?
-The inverse function is a function that reverses the operation of the original function. To find the inverse, you replace f(x) with y, switch x and y, and then solve for y. The inverse function is denoted as f^(-1)(x) or g(x) such that g(f(x)) = x.
How do you determine if two functions are inverses of each other?
-Two functions are inverses of each other if the composite function f(g(x)) equals x and g(f(x)) equals x. This can also be determined graphically by checking if the functions are reflections of each other across the line y = x.
What happens when you have a fraction in a function and the denominator is zero?
-If the denominator of a fraction in a function is zero, the function is undefined at that point. Therefore, the value that makes the denominator zero is excluded from the domain of the function.
How do you handle restrictions on the input of rational functions?
-For rational functions, the denominator cannot be zero. Therefore, the values of x that make the denominator zero are not included in the domain of the function.
What is the process for finding the composite function g(f(x))?
-To find the composite function g(f(x)), you replace the variable in the function g(x) with the expression for f(x). This means you treat f(x) as the input to the function g.
How do you check the validity of a solution for a function using a number line?
-You can check the validity of a solution by plugging the value into the function and seeing if the result satisfies the conditions of the function. If the result is not within the allowed domain or does not meet the function's restrictions, then the solution is not valid.
What is the graphical relationship between a function and its inverse?
-The graph of a function and its inverse are reflections of each other across the line y = x. This means that if you replace the x and y coordinates of every point on the graph of one function with their switched counterparts, you will obtain the graph of the inverse function.
How do you prove that two functions are not inverses of each other?
-To prove that two functions are not inverses of each other, you would show that their composite functions do not simplify to x. If either f(g(x)) or g(f(x)) does not result in x, then the functions are not inverses.
Outlines
📚 Introduction to Composite Functions
This paragraph introduces the concept of composite functions, explaining how they are formed by having one function inside another. It outlines the process of finding the composite function f(g(x)) using examples, and emphasizes the importance of understanding the domain of composite functions. The domain is determined by the input function's restrictions, not the output function's. The paragraph also explains how to represent the domain using interval notation, using a specific example where f(x) = 1/x and g(x) = x + 3.
🔍 Finding Composite Functions and Their Domains
This section delves into the process of finding composite functions and their domains. It provides a step-by-step method for calculating g(f(x)) and emphasizes the need to consider the input function's domain. The paragraph uses the example of f(x) = √(x - 2) and g(x) = 1/(x + 3) to illustrate the process. It also explains how to solve for the domain of the composite function by ensuring the denominator does not equal zero and that the radicand is non-negative for even roots.
🤔 Analyzing Domain Restrictions and Interval Notation
The paragraph focuses on analyzing domain restrictions for composite functions and representing these domains using interval notation. It explains how to handle critical numbers and use a number line to test the validity of the domain. The example provided involves a composite function with a square root and a rational function, highlighting the importance of ensuring the radicand is non-negative and the denominator is non-zero.
🔧 Solving for Composite Functions with Fractions
This part of the script discusses the process of finding composite functions involving fractions and determining their domains. It explains the restrictions on the input function g(x) and how these restrictions affect the domain of the composite function. The example given involves f(x) = √(x - 5) and g(x) = 1/(8 - x), and it illustrates how to solve for the domain by ensuring the denominator does not equal zero and plotting the solution on a number line.
🔄 Understanding Inverse Functions and Their Properties
The paragraph shifts focus to inverse functions, explaining how to find them and use composite functions to determine if two functions are inverses of each other. It outlines the steps for finding the inverse of a function and discusses the graphical relationship between a function and its inverse. The section uses the function f(x) = 3x + 5 and its inverse to demonstrate how to prove two functions are inverses by showing that their composite equals x.
📈 Graphical Verification of Inverse Functions
This section concludes the video script by illustrating how to verify if functions are inverses of each other graphically. It explains that inverse functions are symmetrical about the line y=x. The example provided involves f(x) = ∛(x - 3) and g(x) = x^3 + 3, and it shows that these functions are inverses by calculating their composite functions and simplifying to x. The paragraph wraps up with a summary of the key points discussed in the video.
Mindmap
Keywords
💡composite functions
💡domain
💡interval notation
💡inverse functions
💡rational functions
💡radical functions
💡polynomial functions
💡graphing
💡restrictions
💡number line
💡slope-intercept form
Highlights
The video discusses composite functions, their discovery, domain determination, and their use in testing for inverse functions.
A composite function is formed when one function is nested inside another, with the outer function acting on the inner function's output.
The domain of a composite function is limited by the domain of the input function, not the output function.
For the example of f(x) = 1/x and g(x) = x + 3, the composite function f(g(x)) = 1/(x + 3) is found by substituting g(x) into f(x).
The domain of f(g(x)) is all real numbers except for the value that makes the denominator zero, which in this case is x ≠ -3.
Interval notation is used to represent the domain of composite functions graphically on a number line.
For g(f(x)) determination, the input function's restrictions carry over to the composite function, as seen with f(x) = 1/x and g(x) = x + 3.
When finding composite functions involving radicals, the expression inside the radical must be non-negative.
The domain for composite functions with fractions is determined by ensuring the denominator is not zero.
The video provides a method for finding inverse functions by replacing the function with y, switching x and y, and solving for y.
Inverse functions can be graphically identified by their reflection about the line y = x.
To prove two functions are inverses, one must show that composing them results in the identity function, x.
The video concludes with an example demonstrating that f(x) = cube root(x - 3) and g(x) = x^3 + 3 are indeed inverse functions.
The method for finding composite functions and their domains is demonstrated with clear step-by-step instructions.
The importance of understanding the domain restrictions of both the input and output functions in composite function determination is emphasized.
Practical applications of composite functions in testing for inverse relationships are explored through examples.
The video uses a combination of algebraic manipulation and graphical representation to explain complex mathematical concepts.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: