Harvesting Populations in Differential Equations (Differential Equations 38)
TLDRThe video explores the impact of harvesting and stocking on population models, focusing on differential equations. It explains how these activities can affect critical points and alter population growth, leading to either extinction or explosion. The logistic and explosion-extinction equations are compared, highlighting their differences and the resulting population dynamics. The video emphasizes the importance of sustainable practices to maintain ecological balance.
Takeaways
- 🌿 The impact of harvesting and stocking on population models is significant and has real-world applications, particularly in ecology and biology.
- 📈 The logistic and explosion-extinction differential equations exhibit different behaviors based on the initial population value and the presence of harvesting or stocking.
- 🔄 The logistic equation models a population that decreases if the population is above the carrying capacity (M) and increases if below it.
- 💥 The explosion-extinction equation models a population that increases if above the threshold and goes extinct if below it.
- 🔧 Harvesting or stocking can alter the critical points in population models, affecting the equilibrium solutions and the growth or decline of populations.
- 📊 The critical points in the logistic equation can be easily found, but when harvesting or stocking is introduced, the quadratic formula must be used to determine them.
- 🌐 The bifurcation point is a critical value that separates scenarios of population explosion or extinction, and it depends on the rate of harvesting or stocking.
- 🔄 When the harvesting or stocking rate is less than the bifurcation point, the population model exhibits behavior similar to the logistic model but in reverse.
- 🌍 In real-world scenarios, responsible harvesting and stocking are crucial for maintaining sustainable populations and preventing ecological imbalance.
- 🔢 The quadratic formula is a valuable tool for determining critical points in population models when they are affected by external factors like harvesting or stocking.
- 📈 Understanding the interplay between critical points, population values, and the effects of harvesting and stocking is essential for predicting and managing population dynamics.
Q & A
What is the main focus of the video?
-The main focus of the video is to discuss the impact of harvesting and stocking on critical points and population growth in the context of differential equations, specifically looking at logistic and explosion-extinction models.
What are the two types of differential equations discussed in the video?
-The two types of differential equations discussed are the logistic equation and the explosion-extinction equation.
How do the logistic and explosion-extinction equations differ in terms of their critical points?
-In the logistic equation, the critical point is at M, representing an equilibrium solution. In the explosion-extinction equation, the critical points are at 0 and M, but the behavior around these points is different, with the population exploding above M and going extinct below M.
What is the significance of the bifurcation point in the context of harvesting and stocking?
-The bifurcation point is a critical value of H (harvesting or stocking rate) that determines the number of critical points and the behavior of the population. Above the bifurcation point, the population can either explode or go extinct, at the point, there is a semi-stable equilibrium, and below it, there are two critical points leading to a threshold solution.
How does the initial population value affect the population growth in the logistic equation?
-In the logistic equation, if the initial population value is above M, the population will decrease over time. If the initial value is below M, the population will increase until it reaches the carrying capacity M.
What happens to the population when the harvesting or stocking rate is exactly at the bifurcation point?
-When the harvesting or stocking rate is exactly at the bifurcation point, the population will either go extinct or explode, depending on the initial population value.
What is the role of the quadratic formula in analyzing the critical points of the modified logistic equation?
-The quadratic formula is used to solve for the critical points of the modified logistic equation when the terms are distributed and a quadratic equation is formed. It helps determine the nature and number of critical points based on the value of H (harvesting or stocking rate).
Why is it important to consider the harvesting and stocking rates in population models?
-Considering the harvesting and stocking rates in population models is important because it helps in maintaining the sustainability of the population. Overharvesting can lead to extinction, while overstocking can lead to resource depletion and population collapse.
How does the video script illustrate the real-world application of these population models?
-The video script illustrates the real-world application by discussing scenarios like fishing and wildlife management, where responsible harvesting and stocking practices are crucial for maintaining ecological balance and ensuring the survival of species.
What is the threshold solution in the context of the logistic equation?
-In the context of the logistic equation, the threshold solution refers to the population level (M) where the growth rate is zero. If the initial population is above this level, the population will decrease, and if it's below, the population will increase until it reaches M.
Outlines
🌿 Introduction to Population Models and Harvesting
This paragraph introduces the topic of population models, specifically focusing on how harvesting and stocking affect critical points and population growth. It emphasizes the real-world application of these models in ecology and biology, where sustainable practices are crucial to prevent over-harvesting or extinction of species. The speaker plans to contrast the logistic and explosion-extinction differential equations and their responses to harvesting and stocking.
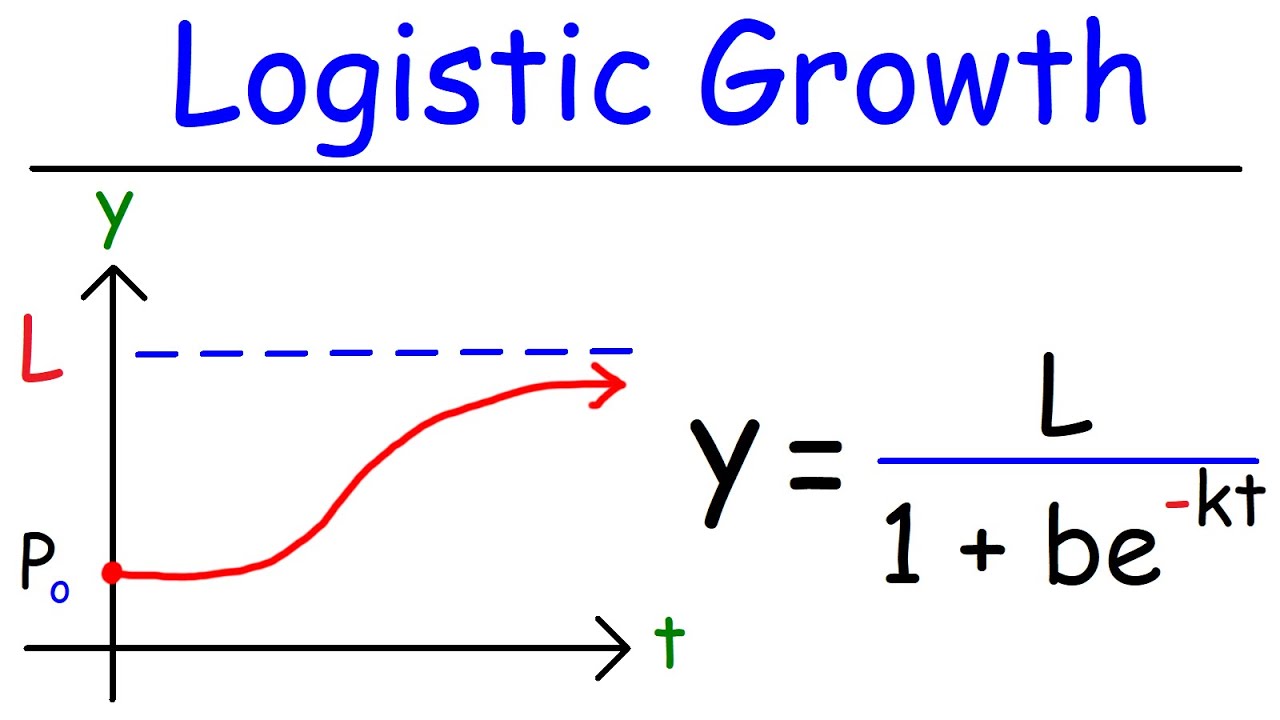
📈 Logistic Equation and Critical Points
The speaker delves into the logistic equation, explaining its relevance to population models and how it creates an equilibrium solution. The critical points of the logistic equation are discussed, with the population's behavior depending on whether it starts above or below the carrying capacity (M). The speaker also highlights the importance of the initial value in determining the population's trajectory and the differences between the logistic and explosion-extinction equations.
🌪️ Explosion-Extinction Equation and Its Dynamics
This section contrasts the logistic equation with the explosion-extinction equation. The speaker explains how the sign difference between the two equations leads to completely different outcomes for population growth. The critical points for the explosion-extinction equation are also discussed, with the speaker noting how the population can either explode or go extinct depending on the initial conditions and the carrying capacity (M).
🔄 Impact of Harvesting and Stocking on Critical Points
The speaker explores the impact of harvesting and stocking on the critical points of population models. By using the quadratic formula, the speaker demonstrates how the presence and nature of critical points are heavily influenced by the harvesting or stocking rate (H). The speaker also introduces the concept of a bifurcation point, where the population can either have two critical points, one critical point, or none at all, depending on the value of H.
📊 Examples and Analysis of Harvesting Scenarios
The speaker provides examples and analysis of different harvesting scenarios, illustrating how the population responds to various levels of harvesting. The speaker emphasizes the importance of understanding the relationship between the harvesting rate (H) and the critical points to ensure sustainable management of populations. The discussion includes the implications of harvesting too much or too little and how it can lead to population extinction or unsustainable growth.
🌟 Conclusion and Reflection on Population Dynamics
In conclusion, the speaker reflects on the importance of understanding population dynamics and the role of harvesting and stocking in maintaining ecological balance. The speaker reiterates the significance of the bifurcation point and how it affects the number of critical points and the behavior of the population. The speaker also encourages viewers to consider the real-life applications of these models, especially in the context of sustainable practices in ecology and resource management.
Mindmap
Keywords
💡Population Models
💡Differential Equations
💡Harvesting
💡Stocking
💡Critical Points
💡Logistic Equation
💡Explosion Extinction Equation
💡Equilibrium Solutions
💡Bifurcation Point
💡Threshold Solution
Highlights
The video discusses the impact of harvesting and stocking on population models, particularly focusing on how these activities affect critical points and population growth.
The distinction between logistic and explosion extinction differential equations is emphasized, noting that slight differences in these models can significantly affect population dynamics.
The logistic equation is described as having a limiting population in equilibrium, with the critical point being M, the carrying capacity.
In the logistic model, if the initial population is above M, the population decreases, and if it's below M, the population increases.
The explosion extinction equation is introduced as the opposite of the logistic equation, with critical points also at zero and M.
For the explosion extinction model, if the initial population is above M, the population explodes, and if it's below M, the population goes extinct.
The video explains how harvesting and stocking activities can be modeled as a constant H in the logistic equation, affecting the critical points and the shape of the population growth curve.
The quadratic formula is used to find the critical points when H is introduced in the logistic equation, showing that the number and nature of critical points depend on the value of H.
A bifurcation point is introduced as a critical value of H where the population model's behavior changes, potentially leading to explosion or extinction of the population.
The video provides a detailed explanation of how different values of H (harvesting or stocking rates) lead to different outcomes for the population, including stable growth, explosion, or extinction.
The importance of sustainable harvesting and stocking practices is emphasized to maintain a healthy and stable population in ecological systems.
The video uses mathematical models to demonstrate the real-world implications of human activities on population dynamics, highlighting the delicate balance needed for sustainable management.
The discussion includes the concept of threshold solutions and semi-stable equilibrium points, which are crucial for understanding how populations respond to changes in environmental conditions and human interventions.
The video concludes with a call to action for responsible management of resources, underlining the importance of understanding and applying mathematical models in real-world scenarios.
The content is rich in mathematical concepts applied to biology, providing a comprehensive understanding of population dynamics and the impact of human activities.
Transcripts
Browse More Related Video

Introduction to Population Models and Logistic Equation (Differential Equations 31)

Population Growth and Decline (Differential Equations 35)

Birth Rates and Death Rates in Differential Equations (Differential Equations 33)

Basic Population Models in Differential Equations (Differential Equations 32)

Equilibrium Solutions and Stability of Differential Equations (Differential Equations 36)
Logistic Growth Function and Differential Equations
5.0 / 5 (0 votes)
Thanks for rating: