Population Growth and Decline (Differential Equations 35)
TLDRThis video delves into population modeling, exploring logistic equations, population explosions, and extinctions through various examples. It explains how birth and death rates affect growth, leading to either limiting populations or carrying capacities. The video emphasizes critical thinking about long-term population trends and uses partial fractions to solve differential equations, revealing insights into population behavior over time and the potential for doomsday scenarios or extinction.
Takeaways
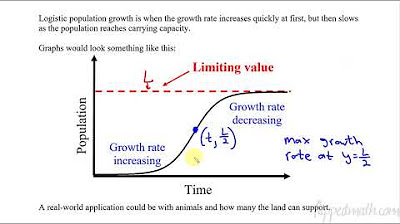
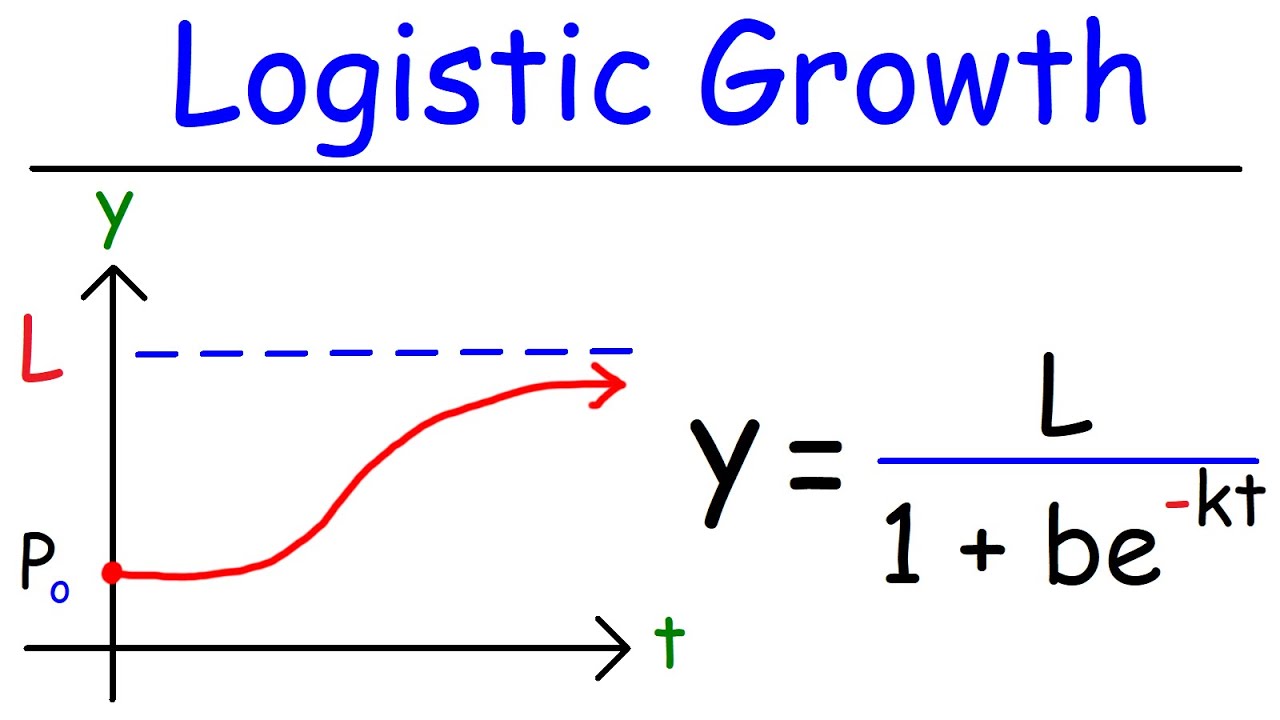
- 📈 The logistic equation is used to model population growth, taking into account factors like birth and death rates, and carrying capacity.
- 🚫 The key difference between logistic growth and exponential growth is the presence of a limiting factor (carrying capacity) in logistic growth.
- 🐾 Population models can predict outcomes such as explosions or extinctions depending on initial conditions and growth parameters.
- 📊 Understanding the rate of change in a population (birth and death rates) is crucial for predicting future population sizes and trends.
- 🌿 The carrying capacity represents the maximum population size that the environment can sustain indefinitely without being degraded.
- 🔢 Partial fraction decomposition is a mathematical technique used to solve complex differential equations, which is applicable in population modeling.
- 🕒 The time it takes for a population to reach a certain size can be calculated by solving the differential equation with given initial conditions.
- 💡 Critical thinking about population models involves considering scenarios beyond the immediate scope of the problem, such as long-term growth or decline.
- 📝 When solving population models, it's important to identify and use initial conditions effectively to find the arbitrary constant in the solution.
- 🌐 Population dynamics are influenced by a complex interplay of factors, and mathematical models help us understand and predict these dynamics.
- 🔍 By analyzing the form of the logistic equation, we can determine whether a population will approach a limit, experience growth explosions, or face extinction.
Q & A
What is the main focus of the video?
-The main focus of the video is to discuss population modeling, specifically looking at logistic equations, population explosions, population extinctions, and carrying capacities through various examples.
What are the two key rates that affect population growth mentioned in the video?
-The two key rates that affect population growth mentioned in the video are birth rates and death rates.
What is the significance of the logistic equation in population modeling?
-The logistic equation is significant in population modeling as it helps to predict how a population will change over time, taking into account factors like carrying capacity and limiting populations.
What is a carrying capacity in population terms?
-A carrying capacity is the maximum population size that the environment can sustain indefinitely without being degraded.
How does the video demonstrate the difference between population growth and carrying capacity?
-The video demonstrates the difference by showing that if the initial population is below the carrying capacity, the population will grow until it reaches that capacity, but if the initial population is above the carrying capacity, the population will decline until it reaches the capacity.
What is the role of partial fractions in solving population equations?
-Partial fractions play a crucial role in solving population equations by allowing the separation of variables and simplification of complex equations, which is essential for understanding and predicting population dynamics.
How does the video emphasize the importance of critical thinking in understanding population models?
-The video emphasizes the importance of critical thinking by encouraging viewers to think beyond the immediate scope of the problem, such as considering what happens when time goes beyond the discussed period or when populations reach their limits.
What is the 'doomsday' scenario mentioned in the video in relation to population growth?
-The 'doomsday' scenario refers to a situation where the population grows uncontrollably, leading to a potential collapse or 'explosion' due to overpopulation and depletion of resources.
How does the video use initial conditions to solve for arbitrary constants in population models?
-The video uses initial conditions, such as the population at time zero and the rate of change of the population at that time, to solve for arbitrary constants in the models. These constants are crucial for making accurate predictions about population growth or decline.
What is the threshold number in the population model discussed in the video?
-The threshold number in the population model discussed in the video is a critical value that determines whether the population will grow (if the initial population is above the threshold) or decline (if the initial population is below the threshold) indefinitely.
Outlines
📈 Introduction to Population Modeling
The video begins with an introduction to population modeling, specifically focusing on the logistic equation. The speaker revisits the concepts of birth and death rates, and how they affect population growth. The aim is to understand population explosions, extinctions, and limiting populations or carrying capacities through three examples. The speaker emphasizes the importance of critical thinking about the long-term implications of these models.
📚 Review of Logistic Equation and Population Dynamics
The speaker reminds viewers of previous videos that discussed the logistic equation and population dynamics, including the concepts of population doomsday and extinction. The focus is on understanding why certain populations reach a plateau or limiting population, and why others might experience growth explosions or extinction. The speaker encourages viewers to think about what happens when time goes beyond the scope of the problem.
🔢 Analyzing Population Growth with Initial Conditions
The speaker delves into the specifics of population growth, using initial conditions to solve for the arbitrary constant in the logistic equation. The discussion includes the rate of change of the population and how it can be used to predict future population sizes. The speaker also introduces the concept of partial fractions and their importance in solving the differential equation.
📊 Partial Fractions and Population Modeling
The speaker explains the process of partial fraction decomposition, which is crucial for solving the population differential equation. The goal is to separate variables and solve for the arbitrary constant using the initial condition. The speaker also discusses the importance of handling signs correctly to avoid common mistakes in calculations.
🕒 Predicting Population Growth Over Time
The speaker demonstrates how to predict population growth over time using the logistic equation. By plugging in the initial population and rate of change, the speaker shows how to solve for the population at a future time point. The discussion also touches on the concept of population explosion and how it can be modeled mathematically.
🤔 Reflecting on Population Dynamics Beyond the Model
The speaker encourages viewers to think beyond the mathematical model and consider the real-world implications of population dynamics. The discussion includes considering what happens when a population reaches its carrying capacity, and the potential for population explosions or extinctions in the long term.
🧬 Birth and Death Rates in Population Modeling
The speaker introduces a new scenario with a population that has a birth rate proportional to the population size and a constant death rate. The speaker uses the given birth and death rates, along with the initial population size, to set up a model for predicting future population changes. The focus is on understanding how birth and death rates interact to affect population growth.
📈 Solving for Death Rate and Population Change
The speaker guides viewers through the process of solving for the constant death rate using the given initial population and rate of change. The speaker then uses this information to set up a differential equation that models the population change over time. The goal is to understand how the birth and death rates contribute to the overall population dynamics.
🌿 Population Growth and the Carrying Capacity
The speaker discusses the concept of carrying capacity and how it relates to population growth. The speaker uses the logistic equation to model a population that starts below its carrying capacity and predicts how the population will grow over time. The discussion includes the idea of a population explosion if the carrying capacity is exceeded.
🚀 Population Explosion and Doomsday Scenario
The speaker presents a doomsday scenario where a population experiences explosive growth leading to a potential crisis. The speaker uses the logistic equation to model this scenario, highlighting the importance of understanding the birth and death rates in predicting such outcomes. The focus is on the mathematical modeling of population dynamics and its real-world implications.
Mindmap
Keywords
💡Logistic Equation
💡Population Growth
💡Carrying Capacity
💡Partial Fractions
💡Differential Equations
💡Birth Rate
💡Death Rate
💡Limiting Population
💡Extinction
💡Exponential Growth
Highlights
The video discusses population modeling using logistic equations, focusing on population explosions, extinctions, and carrying capacities.
The speaker emphasizes the importance of understanding how birth rates and death rates affect population growth dynamics.
Three examples are presented to illustrate the use of partial fractions in population modeling and their interpretations.
The video highlights the critical thinking required to understand the long-term outcomes of population models, beyond the immediate problem scope.
Transcripts
Browse More Related Video

Introduction to Population Models and Logistic Equation (Differential Equations 31)

Birth Rates and Death Rates in Differential Equations (Differential Equations 33)

Harvesting Populations in Differential Equations (Differential Equations 38)

Basic Population Models in Differential Equations (Differential Equations 32)
Calculus BC – 7.9 Logistic Models with Differential Equations
Logistic Growth Function and Differential Equations
5.0 / 5 (0 votes)
Thanks for rating: