8.01x - Lect 11 - Work, Kinetic & Potential Energy, Gravitation, Conservative Forces
TLDRIn this lecture, Professor Walter Lewin explores the concepts of work and energy, focusing on the work-energy theorem and its applications in physics. He explains how work is calculated as the integral of force over displacement and introduces the unit of work, the Joule. The discussion progresses to kinetic energy, potential energy, and the conservation of mechanical energy, emphasizing that the total mechanical energy in a system remains constant if only conservative forces, like gravity, are involved. Lewin uses examples and demonstrations, such as a roller coaster and a pendulum, to illustrate these principles and their real-world implications, reinforcing the importance of understanding energy conservation in physics.
Takeaways
- 📐 The concept of work in physics is defined as the integral of force along the direction of motion, with work being a scalar quantity that can be positive, negative, or zero depending on the direction of the force relative to the motion.
- 💡 The unit of work is the newton-meter (N·m), also known as the joule (J), which represents the amount of energy transferred when a force moves an object.
- 🌟 The work-energy theorem states that the work done by a force on an object as it moves from point A to point B is equal to the change in the object's kinetic energy.
- 📈 Kinetic energy is the energy of motion, given by the formula 1/2 m v^2, where m is the mass and v is the velocity of the object.
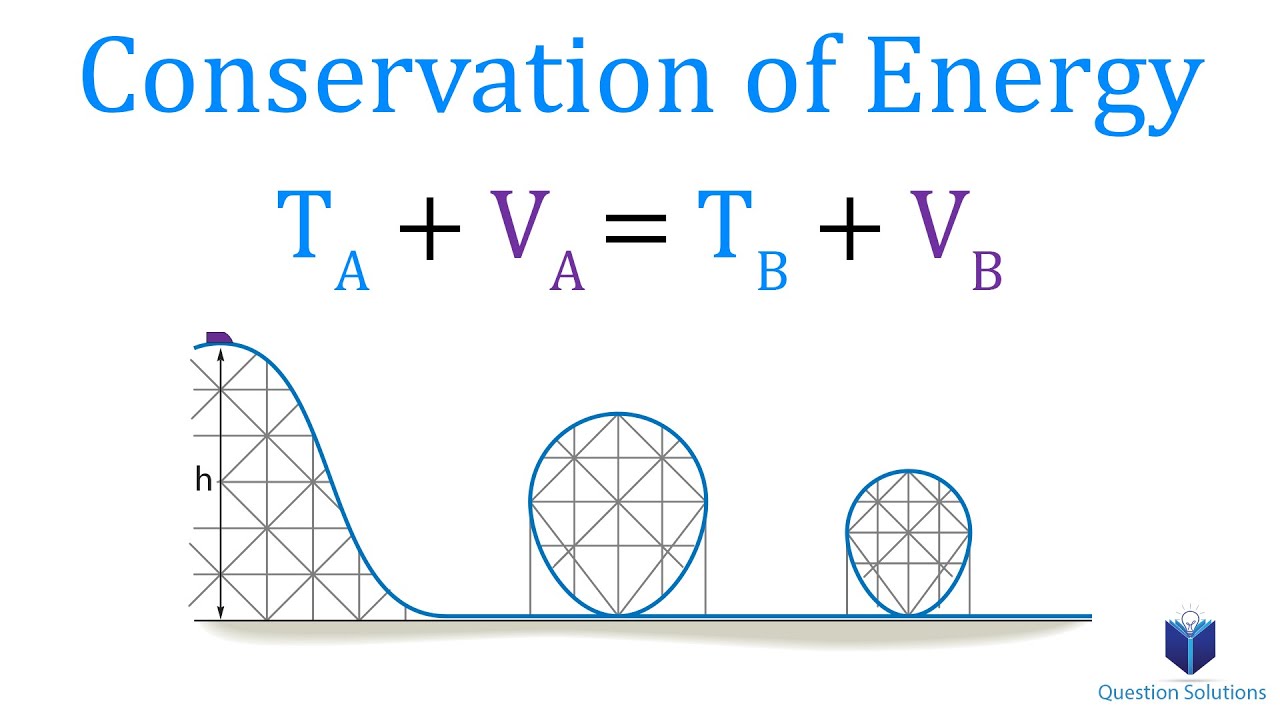
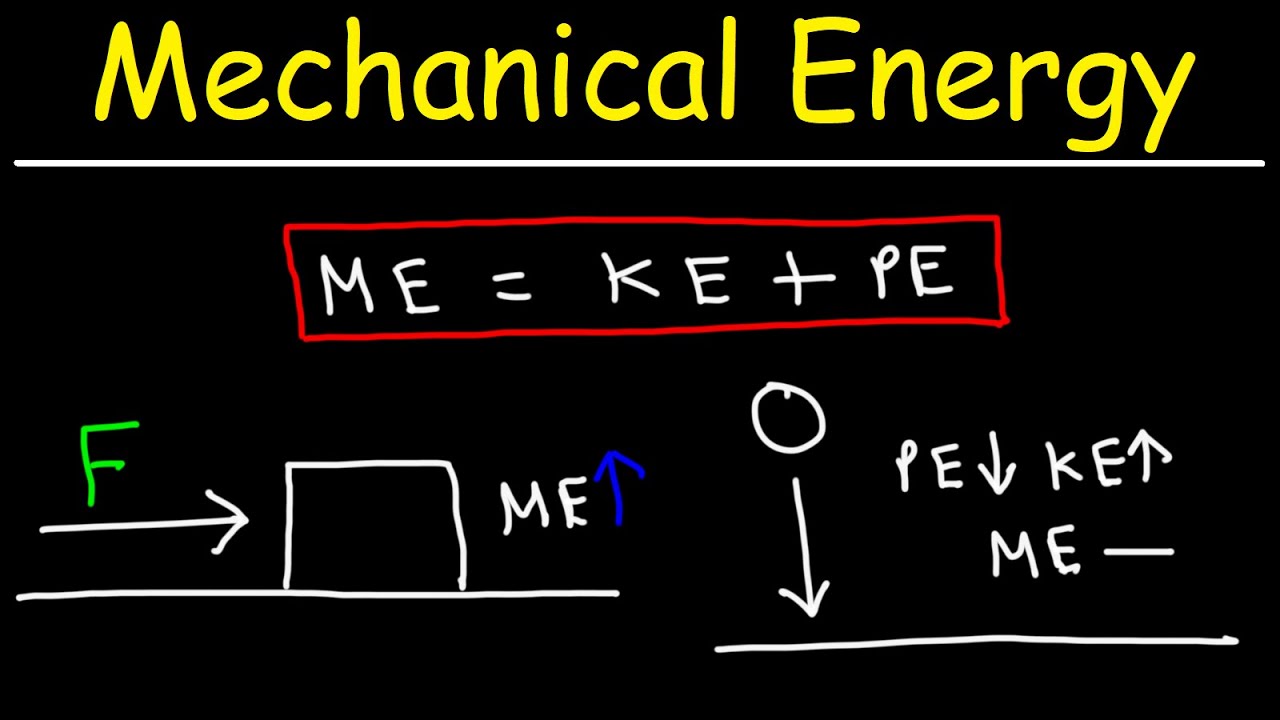
- 🔄 The conservation of mechanical energy principle states that the sum of potential and kinetic energy in a system remains constant when only conservative forces, like gravity, are acting on the system.
- 🎢 The height difference between two points determines the change in gravitational potential energy, with the potential energy at a given height h being mgh, where m is the mass, g is the acceleration due to gravity, and h is the height.
- 🔧 Friction is a non-conservative force, meaning that the work done by friction depends on the path taken and is not conserved in the system.
- 🌐 Gravitational potential energy is defined as the work required to move an object from infinity to a point in a gravitational field, and it is negative for all points within the field, with zero potential energy at infinity.
- 📊 The gravitational potential energy in a gravitational field is given by the equation U = -mGM/R, where m is the mass of the object, G is the gravitational constant, M is the mass of the central body, and R is the distance from the center of the body.
- 🔄 The conservation of mechanical energy allows for the conversion between potential and kinetic energy, but the total mechanical energy remains constant in a closed system with conservative forces.
- 🚀 The concept of gravitational potential energy and its conservation are crucial for understanding the motion of objects in gravitational fields, such as the motion of satellites around planets or the swinging of a pendulum.
Q & A
What is the definition of work in the context of physics?
-In physics, work is defined as the integral of force times displacement (dx) when a force moves an object from point A to point B in a one-dimensional case. The unit of work is newton-meters, also known as a Joule.
How does the direction of the force affect the work done?
-The work done is a scalar quantity and depends on the direction of the force relative to the displacement. If the force and displacement are in the same direction, the work is positive; if they are in opposite directions, the work is negative; and if the force is perpendicular to the displacement, no work is done.
What is the work-energy theorem?
-The work-energy theorem states that the work done by a force on an object is equal to the change in the object's kinetic energy. If the work is positive, the kinetic energy increases; if the work is negative, the kinetic energy decreases; and if the work is zero, there is no change in kinetic energy.
What is the relationship between work, kinetic energy, and potential energy in the context of gravity?
-The work done by gravity is equal to the negative change in gravitational potential energy minus the change in kinetic energy. When an object falls under gravity, gravitational potential energy is converted into kinetic energy, and when it rises against gravity, kinetic energy is converted into gravitational potential energy.
How is gravitational potential energy defined?
-Gravitational potential energy is defined as the work that must be done to move an object from infinity to a point in a gravitational field. It is always negative for all points within a gravitational field and is zero at infinity.
What is the formula for gravitational potential energy in a general case?
-The formula for gravitational potential energy in a general case is U = -mGM/r, where m is the mass of the object, G is the gravitational constant, M is the mass of the source of the gravitational field (like the Earth or the Sun), and r is the distance from the center of the source to the object.
How does the height difference between two points affect the gravitational potential energy?
-The difference in gravitational potential energy between two points is given by the formula ΔU = mgh, where m is the mass of the object, g is the gravitational acceleration at the location of the object, and h is the height difference between the two points.
What is the significance of mechanical energy conservation in physics?
-The conservation of mechanical energy is a fundamental principle stating that the total mechanical energy (the sum of kinetic and potential energy) in an isolated system remains constant when only conservative forces, like gravity, are acting on the system. This principle allows us to predict the behavior of systems in various physical scenarios, such as the motion of a pendulum or the trajectory of a thrown object.
How does friction affect the conservation of mechanical energy?
-Friction is a non-conservative force, meaning it does work that depends on the path taken by the object. When friction is present, mechanical energy is not conserved because some of it is converted into thermal energy, leading to a loss of mechanical energy from the system.
What is the practical application of the conservation of mechanical energy?
-The conservation of mechanical energy has practical applications in various fields, including engineering, where it helps design mechanisms like roller coasters and pendulums, and in the analysis of collisions and the motion of celestial bodies in astronomy.
How does the choice of the zero potential energy level affect calculations?
-The choice of the zero potential energy level is arbitrary and affects the numerical value of potential energy but not the differences in potential energy between two points. This choice does not affect the calculations of work done by conservative forces or the conservation of mechanical energy, as long as the differences in potential energy are consistent.
Outlines
🔧 Work and Energy in One Dimension
This paragraph introduces the concept of work and energy in a one-dimensional context. It explains how work is calculated as the integral of force over distance (newton-meters or Joules) and how it relates to kinetic energy. The work-energy theorem is introduced, stating that the work done by a force on an object is equal to the change in kinetic energy. The paragraph also provides examples of how work can be positive, negative, or zero, depending on the direction of the force relative to the object's motion.
📈 Kinetic Energy and Gravitational Force
The paragraph delves into the relationship between kinetic energy and gravitational force. It demonstrates how the work done by gravity, represented as mgh, is equal to the change in kinetic energy. The concept of height (h) and its effect on gravitational potential energy is explored, leading to the conclusion that the height reached by an object is proportional to the square of its initial velocity divided by 2g. The paragraph also contrasts the work done by an individual (like Walter Lewin) with the work done by gravity, emphasizing the conservation of kinetic energy.
📊 Work in Three Dimensions
This section expands the discussion of work to three-dimensional scenarios. It explains that work is calculated as the dot product of force and displacement (F dot dr), with the force potentially changing direction as it moves through space. The paragraph outlines how to calculate the work done by individual components of force (Fx, Fy, Fz) over a path from point A to B and how this relates to the change in kinetic energy. The concept of conservative forces is introduced, with gravity being a prime example, and the independence of work from the path taken is highlighted.
🌐 Gravitational Potential Energy and Conservation
The paragraph focuses on gravitational potential energy (PE) and its role in the conservation of mechanical energy. It defines PE as the work done against gravity to move an object from infinity to a point in space, with the potential energy at infinity considered zero. The relationship between gravitational potential energy, kinetic energy, and the conservation of mechanical energy is discussed, emphasizing that the sum of these energies remains constant if only conservative forces are at play. The paragraph also touches on the concept of choosing a reference point for zero potential energy and how this choice affects the calculation of potential energy differences.
🎢 Roller Coaster and Mechanical Energy
This paragraph applies the concept of mechanical energy conservation to the real-world scenario of a roller coaster. It explains how an object at the top of a roller coaster has maximum gravitational potential energy, which is converted to kinetic energy as it descends. The paragraph also discusses the critical height from which an object must be released to complete a circular path on the roller coaster, emphasizing the importance of centripetal acceleration and the conservation of mechanical energy in determining whether the object can reach a certain point on the track.
🌍 Gravitational Potential Energy at a Distance
The paragraph addresses the calculation of gravitational potential energy when dealing with large distances, such as in space or when the gravitational acceleration is not constant. It provides the formal definition of gravitational potential energy and explains how to calculate it using the universal law of gravitation. The integral of the gravitational force from infinity to a point at distance R is used to determine the potential energy, resulting in a negative value that increases as the distance from the object increases. The paragraph also clarifies that while near-Earth situations often use mgh as an approximation, the correct formula must be used for large distances.
🏋️♂️ Demonstration of Mechanical Energy Conservation
In this paragraph, a dramatic demonstration of the conservation of mechanical energy is presented. A pendulum with a 15 kg weight is lifted to a height of one meter, storing potential energy, which is then released to convert into kinetic energy as the pendulum swings. The讲师 emphasizes the trust in the principle of energy conservation, even risking a direct hit from the pendulum bob to prove the point. The demonstration successfully illustrates that the pendulum cannot rise higher than its initial height due to the conservation of mechanical energy, reinforcing the concept with a memorable and risky experiment.
Mindmap
Keywords
💡Work
💡Energy
💡Kinetic Energy
💡Potential Energy
💡Conservation of Mechanical Energy
💡Gravitational Force
💡Force
💡Vector
💡Integral
💡Newton's Laws of Motion
💡Dimension
Highlights
Work is defined as the integral of force along the direction of motion.
The unit of work is the newton-meter, also known as the Joule.
When multiple forces act in the same direction, their work is the vector sum of the forces.
Work can be positive, negative, or zero depending on the direction of the force relative to the motion.
The work-energy theorem states that the work done by a force equals the change in kinetic energy.
Kinetic energy is given by 1/2 m v^2.
Gravitational force is mg and can be represented in vector notation as mg y roof.
The work done by gravity is path-independent and is a conservative force.
Gravitational potential energy is given by mgh and is relative to a chosen reference height.
Mechanical energy, the sum of kinetic and potential energy, is conserved when only conservative forces are at play.
Friction is a non-conservative force and its work depends on the path taken.
The roller coaster example demonstrates the conservation of mechanical energy and the minimum height needed to complete a circular path.
Gravitational potential energy is negative and increases as an object moves further from the source of the gravitational field.
The formal definition of gravitational potential energy is the work done to bring a mass from infinity to a point in the field.
Newton's Universal Law of Gravity states that the force between two masses is proportional to the product of their masses and inversely proportional to the square of the distance between them.
The gravitational acceleration experienced by an object is inversely proportional to the square of the distance from the source of gravity.
The general formula for gravitational potential energy in terms of distance is -mGM/R, where M is the mass of the source of gravity and R is the distance from the center of the source.
At infinity, the gravitational potential energy is defined to be zero.
The conservation of mechanical energy principle is fundamental in physics and can be applied to various real-world scenarios, such as a pendulum swinging.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: