2022 Live Review 3 | AP Physics 1 | Understanding Circular Motion and Gravitation
TLDRIn this engaging review session, Brian Brown delves into the dynamics of circular motion and gravitation, focusing on key concepts such as centripetal acceleration and Newton's law of gravitation. Through a series of illustrative examples and practice questions, he clarifies how to analyze the forces involved in circular motion and the gravitational interactions between celestial bodies. The session also emphasizes the importance of understanding the net force in circular motion and applying Newton's second law to solve various physics problems.
Takeaways
- 🌀 Centripetal acceleration is the acceleration experienced by an object moving in a circular path, directed towards the center of the circle, and is responsible for the constant change in direction of the object's velocity.
- 📐 The net force acting on an object in uniform circular motion is always directed towards the center of the circle, causing the centripetal acceleration.
- 🔁 Newton's law of gravitation applies to any two objects, stating that the force of gravity between them is directly proportional to the product of their masses and inversely proportional to the square of the distance between their centers.
- 📊 To determine the net force acting on an object, it is essential to draw a free body diagram, which helps in visualizing and calculating the forces involved.
- 🪁 The gravitational field (g) at a location is defined as the force of gravity experienced by a unit mass placed at that location, and it varies with distance from the mass causing the field.
- 🌍 The acceleration due to gravity (g) on the surface of a planet can be calculated using the formula g = G * (mass of the planet) / (radius of the planet)^2, where G is the universal gravitational constant.
- 🚀 For an object in orbit, the centripetal force required for circular motion is provided by the gravitational force between the object and the central body (e.g., a planet).
- 🛤️ The period of an object in circular motion is the time taken for one complete revolution, and it is related to the speed and radius of the circular path through the formula T = 2πr / v.
- 📈 The relationship between the period and the radius of an orbit can be used to derive the mass of a central body, such as a planet, by analyzing the linearization of the equation T^2 ∝ r^3.
- 🔄 Action and reaction pairs in physics are always equal in magnitude and opposite in direction, as described by Newton's third law, and this principle applies to gravitational interactions as well.
Q & A
What are the key concepts introduced in the session on circular motion and gravitation?
-The key concepts introduced in the session are centripetal acceleration and Newton's law of gravitation.
How does acceleration relate to velocity in circular motion?
-In circular motion, acceleration is involved with changing the direction of an object's velocity, even if the speed remains constant. This type of acceleration is called centripetal acceleration.
What is uniform circular motion?
-Uniform circular motion occurs when an object travels in a circular path with a constant speed. It is a special case of circular motion where the direction of the velocity changes, but not its magnitude.
What is the direction of centripetal acceleration in circular motion?
-Centripetal acceleration is always directed towards the center of the circle in circular motion. It is perpendicular to the velocity of the object at any point in the path.
How is centripetal acceleration related to the speed of an object in circular motion?
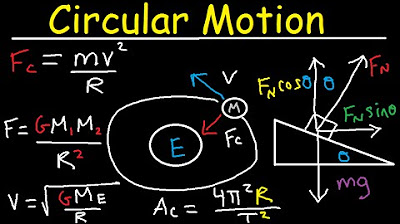
-Centripetal acceleration is proportional to the square of the speed of the object and inversely proportional to the radius of the circular path. The equation for centripetal acceleration is given by ac = v^2 / r, where v is the speed and r is the radius of the circular path.
What is the net force in circular motion?
-The net force in circular motion is the centripetal force that causes centripetal acceleration. It is directed towards the center of the circle and is responsible for changing the direction of the object's velocity.
How does Newton's law of gravitation apply to objects other than those near the Earth's surface?
-Newton's law of gravitation applies to any two objects, regardless of their location. It states that the force of gravity between two objects is directly proportional to the product of their masses and inversely proportional to the square of the distance between them. The gravitational force is given by F = G * (m1 * m2) / r^2, where G is the universal gravitational constant, m1 and m2 are the masses, and r is the distance between the centers of the two objects.
What is the relationship between gravitational field strength (g) and the mass of an object at a distance r from a large mass M?
-The gravitational field strength (g) at a distance r from a large mass M is given by g = G * M / r^2, where G is the universal gravitational constant. This equation shows that the gravitational field strength is directly proportional to the mass of the large object and inversely proportional to the square of the distance from it.
How does the force of gravity change as an object moves farther from the Earth?
-As an object moves farther from the Earth, the force of gravity decreases because it is inversely proportional to the square of the distance between the object and the Earth's center. If the object moves to a distance twice as far from the Earth's center, the gravitational force becomes one-fourth of the force experienced at the surface.
What is the relationship between the period of a revolution and the frequency of revolutions?
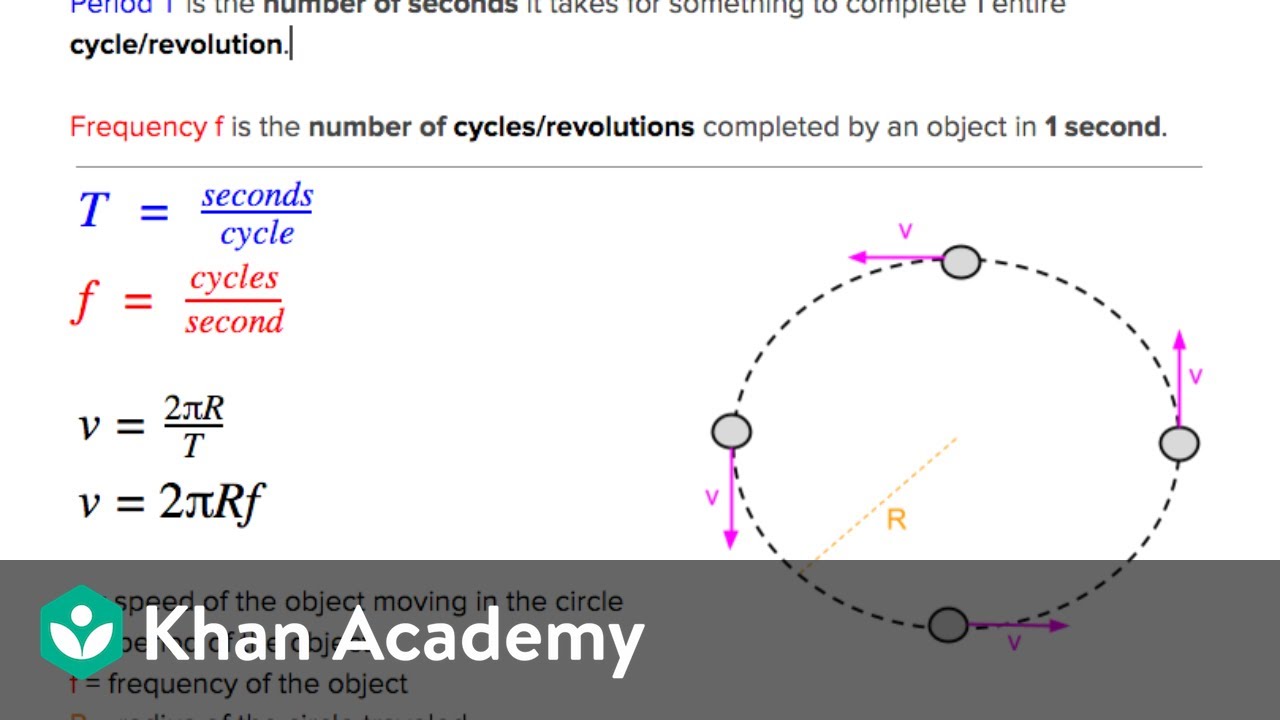
-The period (T) of a revolution is the time taken for one complete revolution, and the frequency (f) is the number of revolutions per second. They are reciprocals of each other, meaning that the period is the inverse of the frequency (T = 1/f) and the frequency is the inverse of the period (f = 1/T).
How can the relationship between the period and the speed of an object in circular motion be derived?
-The speed of an object in circular motion is the distance traveled (circumference of the circle, which is 2πr) divided by the time taken for one revolution (the period, T). Therefore, the speed (v) can be expressed as v = 2πr / T or v = 2πr * f, where f is the frequency of revolutions.
Outlines
📘 Introduction to Circular Motion and Gravitation
The video begins with an introduction to the concepts of circular motion and gravitation, emphasizing the importance of understanding centripetal acceleration and Newton's law of gravitation. The session aims to explore these concepts through the lenses of key terms, definitions, relevant equations, and practical applications. The discussion starts with a review of acceleration, highlighting its role in changing an object's velocity, particularly its direction, which is crucial in circular motion scenarios.
📘 Centripetal Acceleration and Net Force in Circular Motion
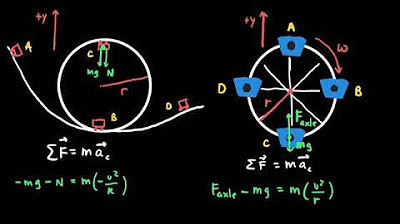
This paragraph delves deeper into the relationship between centripetal acceleration and net force in uniform circular motion. It explains that centripetal acceleration is directly proportional to the square of the speed and inversely proportional to the radius of the circular path. The net force, which can be a combination of various forces, is always directed towards the center of the circle, resulting in centripetal acceleration. The paragraph also presents an example of a yo-yo in vertical circular motion to illustrate how to calculate tension in the string using Newton's second law and the concept of centripetal acceleration.
📘 Period, Frequency, and Gravitational Force
The discussion moves on to define the period and frequency of circular motion, explaining their relationship and how they can be used to derive the speed of an object in circular motion. The paragraph then transitions into an exploration of Newton's law of gravitation, detailing how the force of gravity depends on the masses of two objects and the distance between them. It also touches on how the acceleration of gravity changes as an object moves farther from the Earth's surface.
📘 Gravitational Field and Inverse Square Rule
This section builds on the previous explanation of gravity by focusing on the gravitational field and the inverse square rule. It clarifies that the gravitational field is the force of gravity experienced by a test mass placed in the field and that this field is proportional to the mass of the large object creating it, divided by the square of the distance from the object's center. The paragraph also discusses the implications of the inverse square relationship, showing how the gravitational force decreases as the distance from the object increases.
📘 Gravitational Force Between Multiple Objects
The video script presents a problem involving the gravitational force between three objects, highlighting the principle that any two objects exert a gravitational force on each other. It demonstrates how to calculate the net gravitational force on an object based on the interactions between multiple masses. The paragraph emphasizes the importance of understanding the direction and magnitude of forces to solve such problems accurately.
📘 Circular Motion with an Inclined Plane
This paragraph examines a scenario where an object is spinning around in a horizontal circle on an inclined plane. It identifies the forces acting on the object and explains why the string cannot be completely horizontal due to the balance of forces. The discussion uses trigonometric functions to derive the relationship between the object's speed, the angle of inclination, and the gravitational force.
📘 Gravitational Force and Motion in a Cone
The script explores two different situations involving an object spinning around in a horizontal circle within a cone. The first scenario considers a block released from rest, while the second scenario involves a block moving with a constant velocity. The paragraph contrasts the types of acceleration in each case and uses Newton's second law to analyze the forces involved, including the gravitational force and the normal force from the cone's surface.
📘 Jupiter and its Moons: Gravitational Force and Orbital Motion
This section discusses the application of the universal law of gravitation to the motion of Jupiter's moons. It explains how to calculate the gravitational force between Jupiter and a moon, and how this force can be used to derive the relationship between the period of the moon's orbit and its orbital radius. The paragraph also touches on the concept of linearization to determine the mass of Jupiter from given data.
📘 Summary of Key Concepts and Exam Strategies
The video concludes with a recap of the main concepts covered in the unit, including the principles of centripetal acceleration, net force in circular motion, the gravitational field, and the inverse square rule. It also provides strategies for tackling free-response questions on the AP exam, emphasizing the importance of understanding Newton's second law and the law of gravitation, as well as the ability to apply these concepts to solve problems involving multiple objects and varying distances from a central point.
📘 Upcoming Units and Final Remarks
The script ends with an announcement about the upcoming units, mentioning that the next unit will be introduced by Miss GV, followed by the return of the current instructor for the subsequent unit. The instructor signs off with well wishes for the viewers.
Mindmap
Keywords
💡Centripetal Acceleration
💡Newton's Law of Gravitation
💡Uniform Circular Motion
💡Free Body Diagram
💡Gravitational Field
💡Inverse Square Rule
💡Tangential Velocity
💡Period and Frequency
💡Circular Orbit
💡Linearization
Highlights
Review of key concepts in circular motion and gravitation, including centripetal acceleration and Newton's law of gravitation.
Explanation of how acceleration measures the rate of change in an object's velocity, including changes in direction.
Discussion on uniform circular motion, where the speed remains constant but the direction changes continuously.
Introduction to the relationship between centripetal acceleration, speed, and the radius of the circular path.
Clarification on the net force in circular motion being directed towards the center of the circle, causing centripetal acceleration.
Example of a yo-yo in uniform circular motion and the calculation of tension in the string at the top and bottom of the loop.
Explanation of the period and frequency of circular motion and their relationship to speed and radius.
Derivation of the equation relating speed, period, and radius for uniform circular motion.
Discussion on Newton's law of gravitation and how it applies to any two objects, not just near the Earth's surface.
Explanation of the inverse square rule and how the gravitational force changes with distance.
Illustration of how the gravitational field changes with distance from a large mass, such as a planet.
Use of Newton's second law to calculate the net force and tension in various scenarios involving circular motion.
Analysis of a free response question involving an object in circular motion around a cone and the forces acting on it.
Comparison of gravitational forces between different objects in the solar system, such as Jupiter and its moons.
Demonstration of how to linearize data to determine the mass of celestial bodies like Jupiter.
Ranking of gravitational interactions based on mass and distance, showing the relative strengths of forces between objects.
Summary of the unit's key takeaways, emphasizing the importance of understanding centripetal acceleration and gravitational force in physics.
Transcripts
Browse More Related Video

unit 3 review - Circular motion and gravitation
AP Physics 1 Circular Motion and Gravitation Review

2021 Live Review 3 | AP Physics 1 | Understanding Circular Motion and Gravitation
Centripetal Acceleration & Force - Circular Motion, Banked Curves, Static Friction, Physics Problems
AP Physics 1 review of Centripetal Forces | Physics | Khan Academy

AP Physics 1 - 10 Minute Recap
5.0 / 5 (0 votes)
Thanks for rating: