Introduction to Projectile Motion - Formulas and Equations
TLDRThis video script delves into the equations essential for solving projectile motion problems. It covers the basic kinematic equations for constant speed and acceleration, and introduces the concept of displacement and distance. The script then focuses on three types of projectile motion: horizontal launch from a cliff, angled launch from the ground, and angled launch from an elevated position. It explains how to calculate the height, range, and time of flight for each scenario, using various equations and considering the components of velocity in both horizontal (VX) and vertical (VY) directions. The video also touches on finding the final speed and angle of the projectile just before it hits the ground.
Takeaways
- 📐 Constant speed motion is described by displacement equal to velocity times time.
- 🚀 Constant acceleration motion involves four key equations, including final speed calculations and the relationship between initial speed, acceleration, and time.
- 🎯 In projectile motion, displacement (D) can represent either distance or displacement depending on whether the direction changes.
- 🏞 Understanding the difference between displacement and distance is crucial, especially when dealing with horizontal projectile motion from a cliff.
- 📈 The three types of projectile motion trajectories include horizontal launch from a cliff, angled launch from the ground, and angled launch from an elevated position.
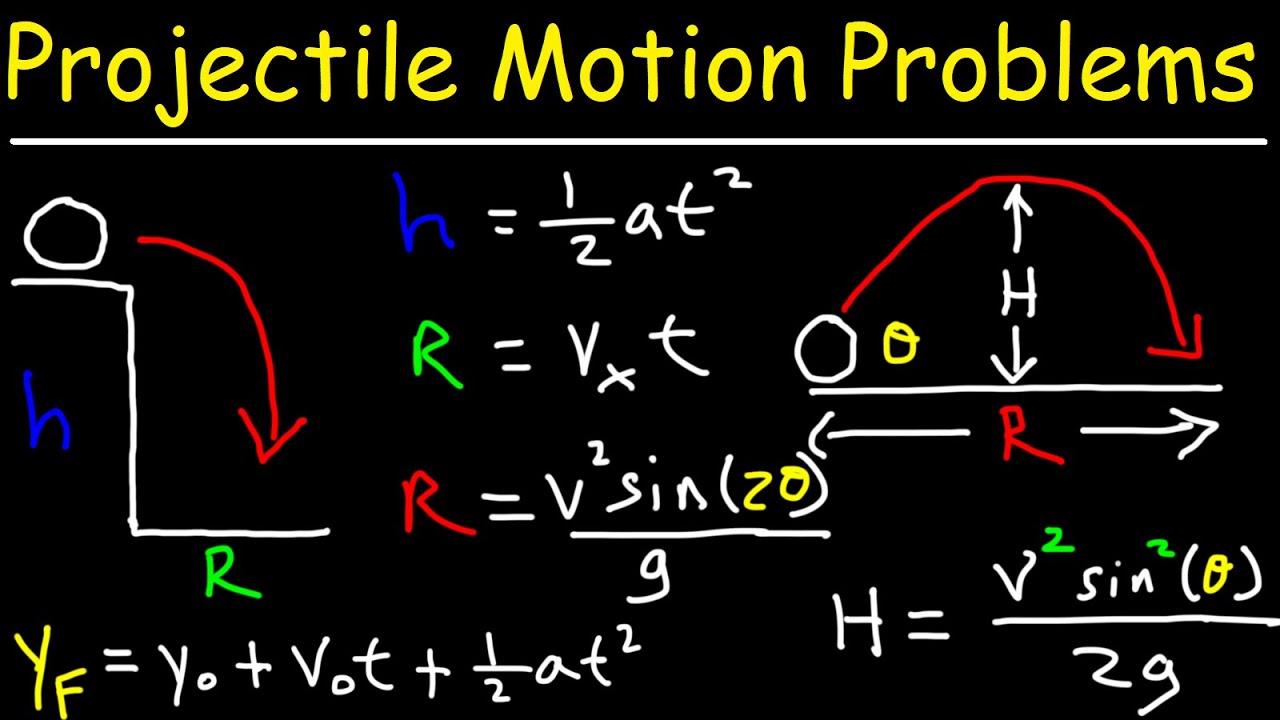
- 🔢 For horizontal projectile motion, use the equation H = 12 * a * t^2 to find the height (H) and range = v_x * t to calculate the horizontal distance (range).
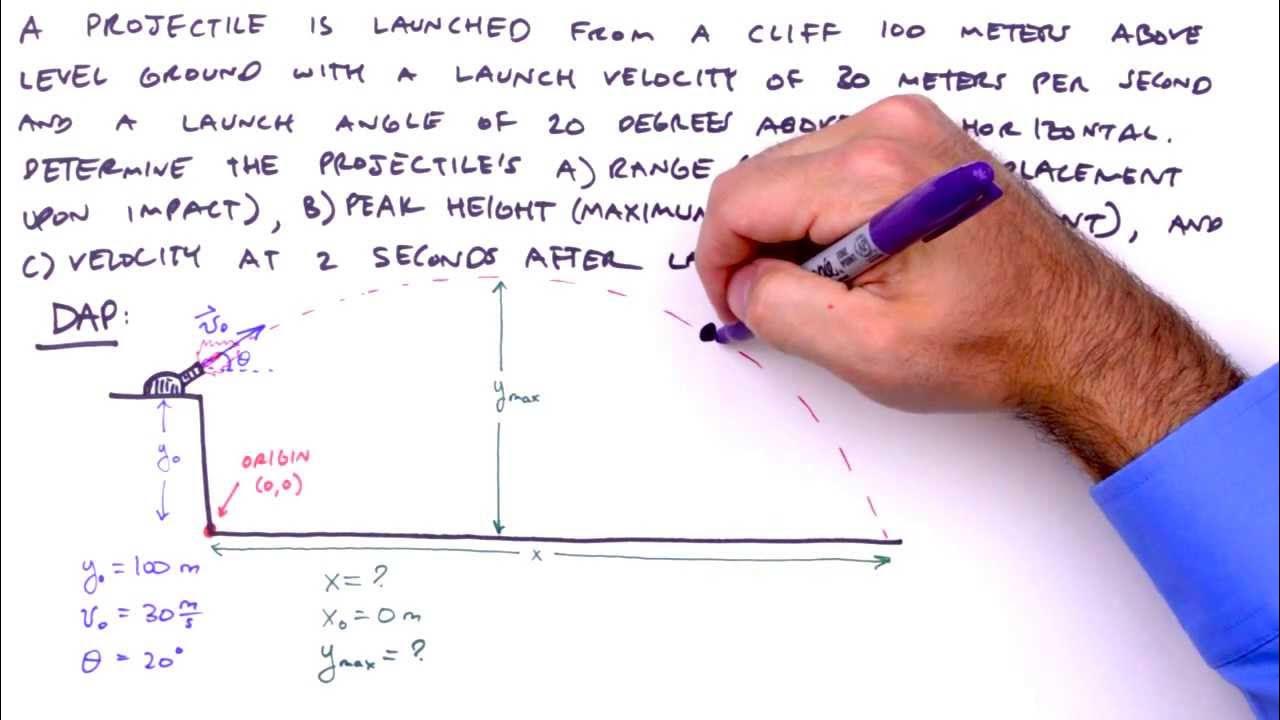
- 🌄 For angled projectile motion from the ground, calculate the time of flight using t = V * sin(Θ) / g and the maximum height with H_max = (V^2 * sin^2(Θ)) / (2 * g).
- 🏞 For projectile motion from an elevated position, calculate the time to hit the ground using quadratic equations or by summing the times for ascending and descending phases.
- 🛤️ The range equation v_x * t is applicable for calculating the horizontal displacement for all trajectories, provided the time is known.
- 🔄 For all trajectories, the horizontal component of velocity (v_x) remains constant, and the vertical component (v_y) is influenced by gravity (g = 9.8 m/s^2).
- 📊 To find the final speed and direction just before impact, combine the horizontal and vertical components of velocity using the inverse tangent function.
Q & A
What are the basic kinematic equations for constant speed and constant acceleration motion?
-For constant speed motion, the displacement is equal to velocity multiplied by time. For constant acceleration motion, the final speed is equal to the initial speed plus the product of acceleration and time, the square of the final speed is equal to the square of the initial speed plus 2 times the product of acceleration and displacement, and displacement is equal to the average speed (initial speed plus final speed divided by 2) multiplied by time.
What is displacement (D) in the context of projectile motion?
-Displacement (D) refers to the change in position of an object, calculated as the difference between the final position and the initial position. In the context of projectile motion, displacement can be used in either the horizontal (X) or vertical (Y) direction, but it's important to note that displacement and distance are not the same unless the object moves in a single direction without changing its path.
What are the three types of projectile motion trajectories discussed in the video?
-The three types of projectile motion trajectories discussed are: 1) Horizontal projectile motion (object launched from a cliff or similar elevated position), 2) Oblique projectile motion (object launched at an angle from the ground), and 3) Projectile motion from an elevated position (object launched at an angle from a cliff or similar height).
How is the height (H) of an object in free fall calculated?
-The height (H) of an object in free fall is calculated using the equation H = 0.5 * g * t^2, where g is the acceleration due to gravity (approximately 9.8 m/s^2) and t is the time it takes for the object to fall to the ground.
What is the equation for the range of a projectile in horizontal motion?
-The equation for the range (R) of a projectile in horizontal motion is R = Vx * t, where Vx is the horizontal component of the initial velocity and t is the time of flight.
How do you calculate the time it takes for a projectile to reach its maximum height?
-The time it takes for a projectile to reach its maximum height is calculated using the equation t = V_y / g, where V_y is the initial vertical velocity (V sin θ) and g is the acceleration due to gravity.
What is the relationship between the initial velocity (V), the horizontal component (Vx), and the vertical component (Vy) of a projectile launched at an angle?
-The horizontal component (Vx) is equal to the initial velocity (V) multiplied by the cosine of the launch angle (θ), and the vertical component (Vy) is equal to the initial velocity (V) multiplied by the sine of the launch angle (θ). The magnitude of the initial velocity (V) is found using the equation V = √(Vx^2 + Vy^2).
How do you find the final speed of a projectile just before it hits the ground?
-To find the final speed of a projectile just before impact, you first determine the horizontal velocity (Vx) which remains constant throughout the motion, and then calculate the final vertical velocity (Vy) using the equation Vy_final = V_y_initial - g * t, where V_y_initial is the initial vertical velocity and t is the total time of flight. The final speed is then found using the equation V_final = √(Vx^2 + Vy_final^2).
What is the significance of the angle (θ) in projectile motion problems?
-The angle (θ) in projectile motion problems represents the angle between the initial velocity vector and the horizontal. It is crucial for determining the horizontal (Vx) and vertical (Vy) components of the initial velocity, which are essential for calculating the trajectory, range, maximum height, and time of flight of the projectile.
How do you describe the angle of the projectile's velocity vector just before it hits the ground?
-The angle of the projectile's velocity vector just before it hits the ground is found using the inverse tangent of the ratio of the vertical component to the horizontal component (arctan(Vy / Vx)). This angle can be described as either below the horizontal or relative to the positive x-axis, depending on the context of the problem.
What is the quadratic formula mentioned in the script used for in projectile motion problems?
-The quadratic formula is used to solve for the time (T) it takes for a projectile to hit the ground in certain scenarios, particularly when the trajectory involves launching from an elevated position. The formula is T = (-b ± √(b^2 - 4ac)) / (2a), where a, b, and c are coefficients derived from the displacement equation in the Y direction, with a representing the acceleration due to gravity (g), b representing the initial vertical velocity (V_y_initial), and c representing the square of the initial vertical velocity minus twice the product of gravity and the initial height.
Outlines
📐 Basic Kinematic Equations for Projectile Motion
This paragraph introduces the fundamental kinematic equations required for solving projectile motion problems. It begins with the basic equation for constant speed motion, where displacement equals velocity times time. It then moves on to describe the equations for constant acceleration, including the final speed equation, the equation relating final speed squared to initial speed squared and acceleration, and the average speed equation. The paragraph emphasizes the importance of understanding these equations for both the X and Y directions in projectile motion analysis.
🏆 Understanding Horizontal and Vertical Motion
The second paragraph delves into the specifics of projectile motion, distinguishing between horizontal and vertical components. It explains the constant horizontal velocity (VX) and the accelerating vertical motion due to gravity (acceleration = 9.8 m/s²). The paragraph covers equations to find the time of flight, maximum height, and range, emphasizing the need to consider the direction (X or Y) when applying these equations. It also introduces the concept of displacement versus distance, highlighting the difference when the direction changes.
🚀 Calculating Speed and Angle for Inclined Trajectories
This paragraph focuses on trajectories where an object is launched at an angle (Theta) to the horizontal. It introduces the vector V, which has both X and Y components, and explains how to calculate these components using the cosine and sine of the launch angle. The paragraph also discusses how to find the time to reach the maximum height and the total time of flight for such trajectories. It concludes with the derivation of an equation for the range of the projectile, incorporating the double-angle formula from trigonometry.
📉 Solving for Time and Range in Various Trajectories
The fourth paragraph continues the discussion on calculating time and range for different projectile trajectories. It provides methods for determining the time it takes for a ball to hit the ground from various heights and the range of the projectile. The paragraph introduces the quadratic formula for solving time in non-symmetrical trajectories and offers an alternative method using the symmetry of the motion. It also explains how to find the final speed and angle of the projectile just before it hits the ground.
🎯 Summary of Equations for Projectile Motion
The final paragraph summarizes the key equations and concepts discussed in the video script. It reiterates the equations for calculating height, range, time, and speed for different types of projectile motion, including horizontal release, angled launch, and elevated starting points. The paragraph emphasizes the importance of applying the correct equations based on the specific characteristics of the trajectory and the need to use positive values in calculations. It concludes by reminding viewers of the significance of understanding these principles for solving projectile motion problems.
Mindmap
Keywords
💡Projectile Motion
💡Kinematic Equations
💡Constant Acceleration
💡Displacement
💡Horizontal and Vertical Components
💡Time of Flight
💡Range
💡Velocity
💡Angle of Launch
💡Gravitational Acceleration
Highlights
Basic kinematic equations for constant speed motion are reviewed, where displacement equals velocity times time.
Four key equations for constant acceleration motion are introduced, including the final speed equation and the displacement equations.
Displacement and distance are differentiated, with displacement being the straight-line distance between initial and final positions.
Three types of projectile motion trajectories are discussed, including horizontal projectile motion, angled projectile motion, and projectile motion from an elevated position.
The equation for the height of a projectile motion (H = 12at^2) is derived and explained.
The range of a projectile motion is calculated using the equation R = v_x * t, where v_x is the horizontal component of the initial velocity.
The speed of the ball just before it hits the ground is determined by combining the horizontal and vertical components of velocity.
The angle of the ball's velocity just before impact is found using the inverse tangent of the vertical speed divided by the horizontal speed.
For angled projectile motion, the time to reach the maximum height is calculated using t = (V * sin(Theta)) / G.
The maximum height reached in angled projectile motion is given by the equation H_max = (V^2 * sin^2(Theta)) / (2G).
The range of angled projectile motion is derived using the equation R = (v^2 * sin(2Theta)) / G, applying trigonometric relationships.
For projectile motion from an elevated position, the time to hit the ground is found using a quadratic equation or by summing the times for two symmetrical segments of the trajectory.
The range equation for projectile motion from an elevated position is R = V * cos(Theta) * T, emphasizing the importance of using the correct trajectory equation.
The final vertical speed component just before impact is calculated using the equation VY_final = V * sin(Theta) - G * T, highlighting the symmetry of the trajectory.
The angle of the ball's velocity relative to the horizontal just before impact can be described as either below the horizontal or positive relative to the x-axis, depending on the context.
The video concludes with a review of the main equations for each type of projectile motion, emphasizing the need to understand when to apply each equation.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: