Regents Physics: Angled Projectile Problem Practice

Dan Fullerton
22 Oct 201108:24
EducationalLearning
32 Likes 10 Comments

TLDRThe transcript discusses two projectile motion problems involving an initial launch at an angle. The first problem calculates the horizontal distance traveled by a human cannonball before landing, using the initial velocity's horizontal and vertical components and the time in the air. The second problem finds the maximum height reached by a ball kicked at an angle, using the vertical component of the initial velocity and the total flight time. Both problems utilize kinematic equations and trigonometry to solve for displacement and height.

Takeaways
  • 🚀 The problem involves projectile motion with an object (Hermann the human cannonball) launched at an angle above the horizontal.
  • 🎯 Hermann is launched from level ground at an angle of 30 degrees with an initial velocity of 26 m/s.
  • 📐 The goal is to find the horizontal distance Hermann travels before returning to the ground.
  • 🔢 The initial velocity is broken down into horizontal (22.5 m/s) and vertical (13 m/s) components using trigonometry.
  • 🕒 The time Hermann spends in the air is calculated by analyzing the vertical motion, resulting in a total time of 2.66 seconds.
  • 🏃 The horizontal distance is determined by multiplying the average horizontal velocity by the total time in the air, resulting in 59.6 meters.
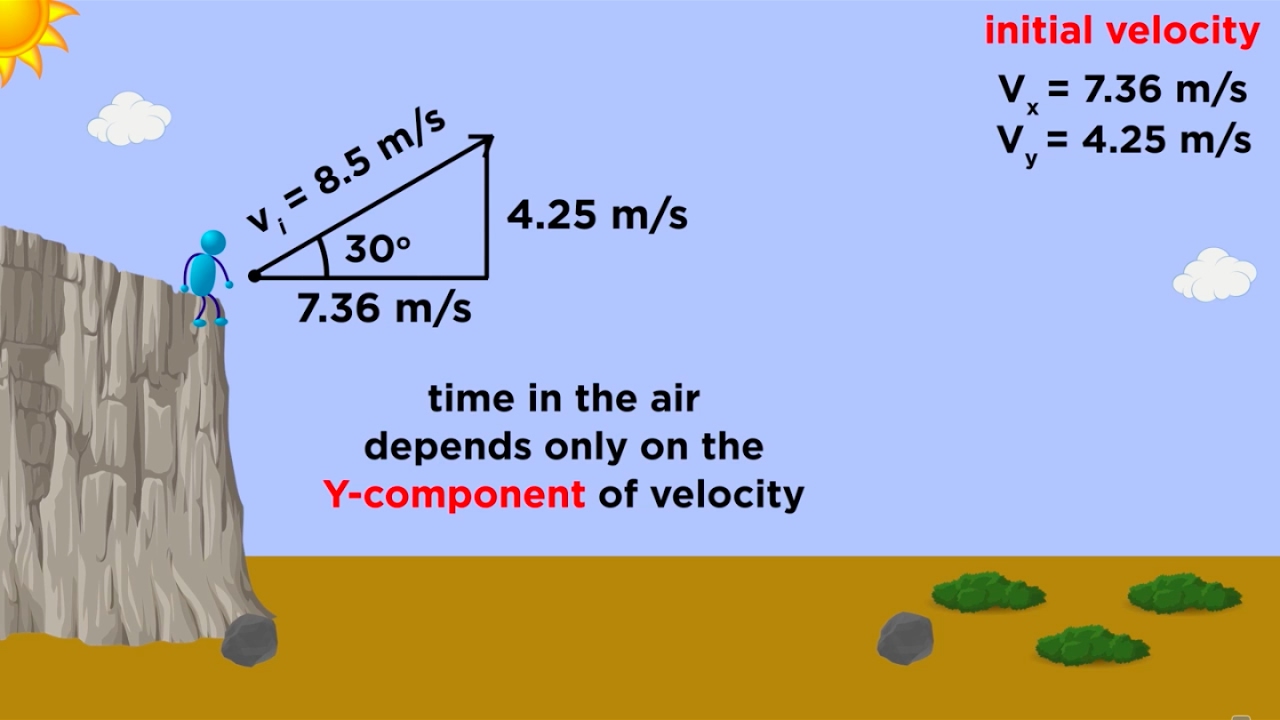
  • 👶 Another problem involves a ball kicked with an initial velocity of 8.5 m/s at an angle of 35 degrees above the horizontal.
  • ⏱ The ball's total flight time is given as one second, and air resistance is neglected.
  • 📈 The maximum height reached by the ball is calculated using the kinematic equation, yielding approximately 1.2 meters.
  • 📊 The key to solving these problems is breaking down the motion into horizontal and vertical components and applying the appropriate kinematic equations.
  • 📚 Trigonometry plays a crucial role in determining the initial velocity components in both horizontal and vertical directions.
Q & A

  • What is the initial velocity of Hermann the human cannonball?

    -Hermann's initial velocity is 26 meters per second.

  • At what angle is Hermann launched relative to the horizontal?

    -Hermann is launched at an angle of 30 degrees above the horizontal.

  • What is the horizontal component of Hermann's initial velocity?

    -The horizontal component of Hermann's initial velocity is approximately 22.5 meters per second.

  • What is the vertical component of Hermann's initial velocity?

    -The vertical component of Hermann's initial velocity is approximately 13 meters per second.

  • What is the total time Hermann spends in the air?

    -Hermann spends a total of 2.66 seconds in the air.

  • How far does Hermann travel horizontally before hitting the ground?

    -Hermann travels approximately 59.6 meters horizontally before hitting the ground.

  • What is the initial velocity of the ball in the second problem?

    -The initial velocity of the ball is 8.5 meters per second.

  • What is the angle at which the ball is kicked in the second problem?

    -The ball is kicked at an angle of 35 degrees with the horizontal.

  • What is the total flight time of the ball?

    -The total flight time of the ball is one second.

  • What is the maximum height reached by the ball?

    -The maximum height reached by the ball, neglecting air resistance, is about 1.2 meters.

  • How is the initial velocity vector broken down in these problems?

    -The initial velocity vector is broken down into horizontal and vertical components using trigonometry, specifically cosine and sine functions.

  • What is the key to solving these projectile motion problems?

    -The key to solving these problems is breaking down the motion into horizontal and vertical components and using the appropriate kinematic equations to analyze each component separately.

Outlines
00:00
🚀 Hermann the Human Cannonball's Horizontal Journey

This paragraph discusses the physics of projectile motion, specifically focusing on the horizontal distance traveled by Hermann the human cannonball. Hermann is launched from level ground at a 30-degree angle with an initial velocity of 26 meters per second. The key to solving the problem is understanding the horizontal and vertical components of his velocity. The horizontal component is calculated by multiplying the initial velocity by the cosine of the angle, resulting in approximately 22.5 m/s. Since air resistance is neglected, this becomes Hermann's constant horizontal velocity. The vertical component of the initial velocity is determined by multiplying the initial velocity by the sine of the angle, which is about 13 m/s. By analyzing the time Hermann takes to reach the highest point in his trajectory, we can calculate his total time in the air. Using the average horizontal velocity and total time, we can then find the horizontal distance traveled, which is approximately 59.6 meters.

05:04
🏐 Ball's Maximum Height in Projectile Motion

The second paragraph delves into another projectile motion scenario, this time with a child kicking a ball at an initial velocity of 8.5 m/s at a 35-degree angle to the horizontal. The main focus here is to find the maximum height reached by the ball during its flight, with air resistance being neglected. The ball's initial vertical velocity is given as 4.9 m/s, and the total flight time is one second. To find the maximum height, the problem is approached by analyzing the vertical motion, using the kinematic equation that relates final velocity (which is zero at the peak), initial velocity, and displacement with acceleration due to gravity. By rearranging the equation and solving for displacement, the maximum height is calculated to be approximately 1.2 meters. The key takeaway is the importance of breaking down the initial velocity into its vertical and horizontal components and focusing on the relevant motion (in this case, the vertical) to solve the problem.

Mindmap
Keywords
💡Projectile Motion
Projectile motion refers to the motion of an object that is launched into the air and moves under the influence of gravity and air resistance. In the video, it is the main theme as it discusses problems related to the motion of Hermann the human cannonball and a kicked ball. The analysis of their trajectories, both horizontal and vertical components, is central to solving the problems presented.
💡Initial Velocity
Initial velocity is the speed at which an object begins its motion. It is a crucial parameter in projectile motion problems as it determines the object's path and distance traveled. In the video, the initial velocities of Hermann and the ball are given as 26 m/s and 8.5 m/s, respectively, and are used to calculate their horizontal and vertical displacements.
💡Angle of Launch
The angle of launch is the angle between the initial velocity vector and the horizontal direction when the object is projected. It is a key factor in determining the trajectory of the object and affects both the range and the maximum height achievable. In the video, angles of 30 degrees and 35 degrees are used for Hermann and the ball, respectively.
💡Horizontal and Vertical Components
In projectile motion, the initial velocity can be decomposed into horizontal and vertical components. The horizontal component (Vx) remains constant throughout the motion, while the vertical component (Vy) changes due to acceleration caused by gravity. These components are essential for analyzing the motion separately along the X and Y axes and for solving problems like the ones discussed in the video.
💡Acceleration due to Gravity
Acceleration due to gravity is the constant acceleration that objects experience near the Earth's surface, directed downwards. It is typically denoted by 'g' and has a value of approximately 9.81 m/s^2. In the context of the video, this acceleration affects the vertical motion of Hermann and the ball, causing them to ascend and then descend.
💡Time of Flight
Time of flight is the total duration an object spends in the air during projectile motion. It is crucial for determining the object's total distance traveled horizontally and the maximum height reached. In the video, the time of flight is calculated for Hermann and used to find out how far he travels horizontally and the time the ball is in the air to find its maximum height.
💡Trigonometry
Trigonometry is a branch of mathematics that deals with the relationships between the angles and sides of triangles, particularly right-angled triangles. In the context of the video, trigonometry is used to break down the initial velocity into its horizontal and vertical components using sine and cosine functions.
💡Kinematic Equations
Kinematic equations are mathematical relationships that describe the motion of objects without considering the forces that cause the motion. They relate displacement, velocity, acceleration, and time. In the video, kinematic equations are used to analyze the motion of Hermann and the ball, particularly to find the time of flight and the horizontal distance traveled.
💡Maximum Height
Maximum height is the highest point reached by an object in its trajectory during projectile motion. It is a key parameter in analyzing vertical motion. In the video, the maximum height is calculated for the ball using the vertical component of its initial velocity and the acceleration due to gravity.
💡Horizontal Distance
Horizontal distance is the total length of the path traveled by an object in the horizontal direction during its motion. It is a key parameter in analyzing the range of projectile motion. In the video, the horizontal distance is calculated for Hermann using his horizontal velocity and time of flight.
💡Air Resistance
Air resistance is the force that opposes the motion of an object through the air. It is often neglected in simple projectile motion problems to focus on the effects of gravity alone. In the video, air resistance is neglected when calculating the maximum height of the ball, simplifying the analysis.
Highlights

Projectile motion problems are discussed, specifically focusing on the horizontal and vertical components of the motion.

Hermann the human cannonball is used as an example to illustrate the concepts of projectile motion.

Hermann is launched at a 30-degree angle above the horizontal with an initial velocity of 26 meters per second.

The problem-solving approach involves breaking down the initial velocity into its horizontal and vertical components using trigonometry.

The horizontal component of Hermann's velocity is calculated to be approximately 22.5 meters per second.

The vertical component of the initial velocity is found to be about 13 meters per second.

Hermann's total time in the air is determined to be 2.66 seconds.

Using the average horizontal velocity and total time, Hermann's horizontal distance is calculated to be approximately 59.6 meters.

The second problem involves a ball kicked at an angle above the horizontal with a given initial velocity and flight time.

The ball's initial vertical velocity is given as 4.9 m/s, and the flight time is one second.

The maximum height reached by the ball is calculated by analyzing the vertical motion and using the kinematic equation.

The maximum height is found to be approximately 1.2 meters, neglecting air resistance.

The importance of understanding the horizontal and vertical separation in analyzing projectile motion is emphasized.

The use of trigonometry to break down the initial velocity vector into components is highlighted as a crucial step in solving these problems.

The practical application of these concepts is demonstrated through the use of real-world examples, such as a human cannonball and a kicked ball.

The process of solving these problems is outlined, providing a clear methodology for tackling projectile motion scenarios.

Transcripts

Browse More Related Video

Projectile Motion: Shooting a Basketball Problem

Physics 3.5.4h - Projectile Practice Problem 8

Consolidation: Projectile Motion Calculations

How To Solve Any Projectile Motion Problem (The Toolbox Method)

Kinematics Part 3: Projectile Motion

Projectile launched off a cliff at an angle

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
PhysicsProjectile MotionTrigonometryKinematicsHuman CannonballKicked BallHorizontal DistanceMaximum HeightEducationalScience