Projectile Motion (AP Physics 1)

Physics Done Phast
3 Jun 202003:36
EducationalLearning
32 Likes 10 Comments

TLDRThis script introduces the concept of projectile motion, a fundamental topic in AP Physics 1. It explains that an object's motion can be broken down into independent horizontal and vertical components, each with constant velocity or acceleration, respectively. The video script simplifies the analysis by using basic trigonometry to separate these components and derives essential equations for solving projectile motion problems, such as range, maximum height, and the object's height as a function of horizontal displacement. The script emphasizes the symmetry of projectile motion and the importance of considering the direction of velocities and acceleration due to gravity.

Takeaways
  • 📚 The script discusses the fundamentals of 2D motion, specifically focusing on projectile motion, which is a common topic in AP Physics 1.
  • 🚀 Projectile motion involves an object moving with both horizontal (X) and vertical (Y) velocity components, resulting in a parabolic trajectory.
  • 🔍 The horizontal and vertical components of motion are independent, allowing for separate analysis using basic kinematic equations.
  • 🌐 In the absence of air resistance, the horizontal motion is characterized by constant velocity, simplifying the kinematic equations for the X direction.
  • 🌍 The vertical motion is a constant acceleration problem, with gravity (9.8 m/s²) acting downwards, which is represented with a negative sign in calculations.
  • ⏱ The total time of flight for a projectile can be determined by considering the symmetry of the vertical motion and the effects of gravity.
  • 📏 The range, or horizontal distance traveled by the projectile, can be calculated using the horizontal velocity and the total time of flight.
  • 📈 The maximum height of the projectile's trajectory is reached at the midpoint of the total time of flight, due to the parabolic shape of the path.
  • 🔢 An advanced equation is presented that allows for calculating the height of the projectile as a function of horizontal displacement, providing a detailed view of the object's path.
  • 🛑 While the advanced equation is complex and not essential to memorize, it can be a valuable tool for quickly solving problems in exams.
  • 🎓 The script concludes by reinforcing the importance of understanding projectile motion, which is a key concept in AP Physics 1.
Q & A

  • What is the most common type of kinematic question in AP Physics 1 after 1D kinematics?

    -The most common type of kinematic question in AP Physics 1 after 1D kinematics is projectile motion.

  • How is the velocity vector of an object in projectile motion described?

    -The velocity vector of an object in projectile motion has both an X (horizontal) and Y (vertical) component.

  • Why is gravity considered in projectile motion?

    -Gravity is considered in projectile motion because it pulls the object down towards Earth, affecting the vertical component of its motion and creating a parabolic arc.

  • How are the horizontal and vertical components of an object's motion related in projectile motion?

    -The horizontal and vertical components of an object's motion in projectile motion are completely independent.

  • What is the acceleration along the horizontal axis in projectile motion without air resistance?

    -In projectile motion without air resistance, there is no acceleration along the horizontal axis, meaning the horizontal motion follows a constant velocity scenario.

  • What is the acceleration in the vertical direction for an object in projectile motion?

    -The acceleration in the vertical direction for an object in projectile motion is the acceleration due to gravity, which is 9.8 meters per second squared, directed downwards.

  • Why is it important to assign the correct signs to velocities directed up and down in projectile motion?

    -It is important to assign the correct signs to velocities directed up and down in projectile motion to accurately represent the direction of motion and ensure the equations are solved correctly.

  • What is the symmetry property of the vertical component of an object's velocity in projectile motion?

    -The symmetry property of the vertical component of an object's velocity in projectile motion is that it ends up being the opposite of its original value.

  • How can you find the total time an object is in motion during projectile motion?

    -You can find the total time an object is in motion during projectile motion by using the equation that relates acceleration (due to gravity) to the change in velocity.

  • What is the range equation in projectile motion, and how does it relate to the horizontal component of motion?

    -The range equation in projectile motion calculates the total horizontal distance the object travels. It is found using the constant horizontal velocity V_sub_X and the total time of flight.

  • At what point in projectile motion does the object's peak height occur, and how does this relate to the time of flight?

    -The object's peak height occurs at half of the total time of flight due to the symmetry of its parabolic path.

  • How can you find the maximum height of an object's trajectory in projectile motion?

    -You can find the maximum height of an object's trajectory in projectile motion by plugging the time at which the peak height occurs (half of the total time of flight) into the kinematic equation used for the vertical direction.

  • What is the significance of the equation that allows you to find the height of an object as a function of its horizontal displacement?

    -This equation is significant because it allows you to determine the height of an object at any given horizontal position (X), effectively showing the object's actual path or trajectory.

Outlines
00:00
🚀 Introduction to 2D Kinematics and Projectile Motion

This paragraph introduces the concept of analyzing the motion of objects in two dimensions, focusing on projectile motion as a common topic in AP Physics 1. The script explains that projectile motion can be understood by breaking it down into horizontal (X) and vertical (Y) components, which are independent of each other. The horizontal motion is characterized by constant velocity due to the absence of air resistance, while the vertical motion is a constant acceleration scenario due to gravity. The paragraph emphasizes the importance of understanding these components separately and applies basic kinematic equations to each to solve projectile motion problems.

Mindmap
Keywords
💡1D Kinematics
1D Kinematics refers to the study of the motion of objects along a single dimension, typically a straight line. It is a foundational concept in physics that deals with displacement, velocity, and acceleration within a one-dimensional space. In the video, it serves as a preface to the more complex topic of 2D motion, providing a basis for understanding the principles that apply to objects moving in multiple directions.
💡2D Motion
2D Motion involves the analysis of an object's movement in two dimensions, which includes both horizontal and vertical components. It is a step up from 1D kinematics and is essential for understanding more complex real-world scenarios like projectile motion. The script introduces 2D motion as the primary focus for analyzing the trajectory of objects such as a basketball shot or a tennis ball thrown.
💡Projectile Motion
Projectile Motion is a specific type of 2D motion where an object is projected into the air and moves under the influence of gravity, following a parabolic trajectory. The script emphasizes that projectile motion is a common topic in AP Physics 1 and is fundamental to understanding how objects move when thrown or launched.
💡Velocity Vector
A Velocity Vector is a mathematical representation of an object's velocity, which includes both the speed and direction of the object. In the context of the video, the velocity vector of a projectile has both horizontal (X) and vertical (Y) components. Understanding these components is crucial for analyzing the object's motion in two dimensions.
💡Horizontal Component
The Horizontal Component refers to the part of an object's motion that occurs along the horizontal axis (X-axis). In the script, it is explained that in the absence of air resistance, the horizontal motion of a projectile follows a constant velocity scenario, making it relatively straightforward to analyze.
💡Vertical Component
The Vertical Component is the part of an object's motion that occurs along the vertical axis (Y-axis). The script mentions that the vertical motion is influenced by gravity, which acts downwards, causing acceleration. This component is key to understanding the height and parabolic path of a projectile.
💡Constant Acceleration
Constant Acceleration is a term used to describe a situation where an object's acceleration remains unchanged over time. In the video, it is used to describe the vertical motion of a projectile, where gravity provides a constant acceleration of 9.8 m/s² downwards.
💡Symmetry
Symmetry in the context of projectile motion refers to the property where the upward and downward paths of the projectile are mirror images of each other. The script uses the concept of symmetry to explain that the vertical component of the object's velocity at the end of its motion is the opposite of its initial value.
💡Range Equation
The Range Equation is a formula used to calculate the horizontal distance traveled by a projectile from the point of projection to the point of landing. The script mentions this equation in the context of finding the total horizontal distance the object travels during its motion.
💡Maximum Height
Maximum Height is the highest point reached by a projectile in its trajectory. The script explains that the peak height of the projectile's path can be calculated using the kinematic equations for the vertical component of motion, and it occurs at half the total time of flight due to the symmetry of the projectile's path.
💡Height Function
Height Function refers to an equation that describes the height of a projectile as a function of its horizontal displacement. The script presents this as a complex but useful equation for determining the exact position of a projectile at any point along its trajectory, effectively graphing the object's path.
Highlights

Understanding 1D kinematics is fundamental before analyzing 2D motion.

Projectile motion involves objects with both horizontal (X) and vertical (Y) velocity components.

Gravity affects the vertical motion, creating a parabolic trajectory.

Horizontal and vertical motion components are independent of each other.

Horizontal motion is a constant velocity scenario due to the absence of air resistance.

Vertical motion is a constant acceleration problem with gravity as the acceleration.

The negative sign of gravity is crucial as it is directed downwards.

Projectile motion equations can be derived for objects starting and ending at the same height.

The vertical component of an object's velocity ends up being the opposite of its original value due to symmetry.

Total time of projectile motion can be calculated using the rate of change of velocity.

The range or total horizontal distance can be found using the horizontal velocity and time.

The object's peak height occurs at half the total time due to the symmetry of its path.

The maximum height of the trajectory can be solved using the kinematic equation for the vertical direction.

A complex equation can determine the height of an object as a function of its horizontal displacement.

This equation essentially graphs the object's actual path, useful for quick problem-solving.

Separating components is key to solving projectile motion problems.

Transcripts

Browse More Related Video

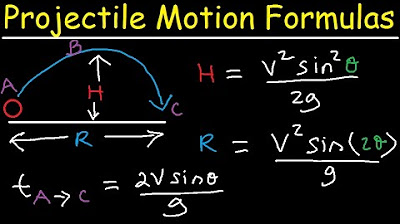
Introduction to Projectile Motion - Formulas and Equations

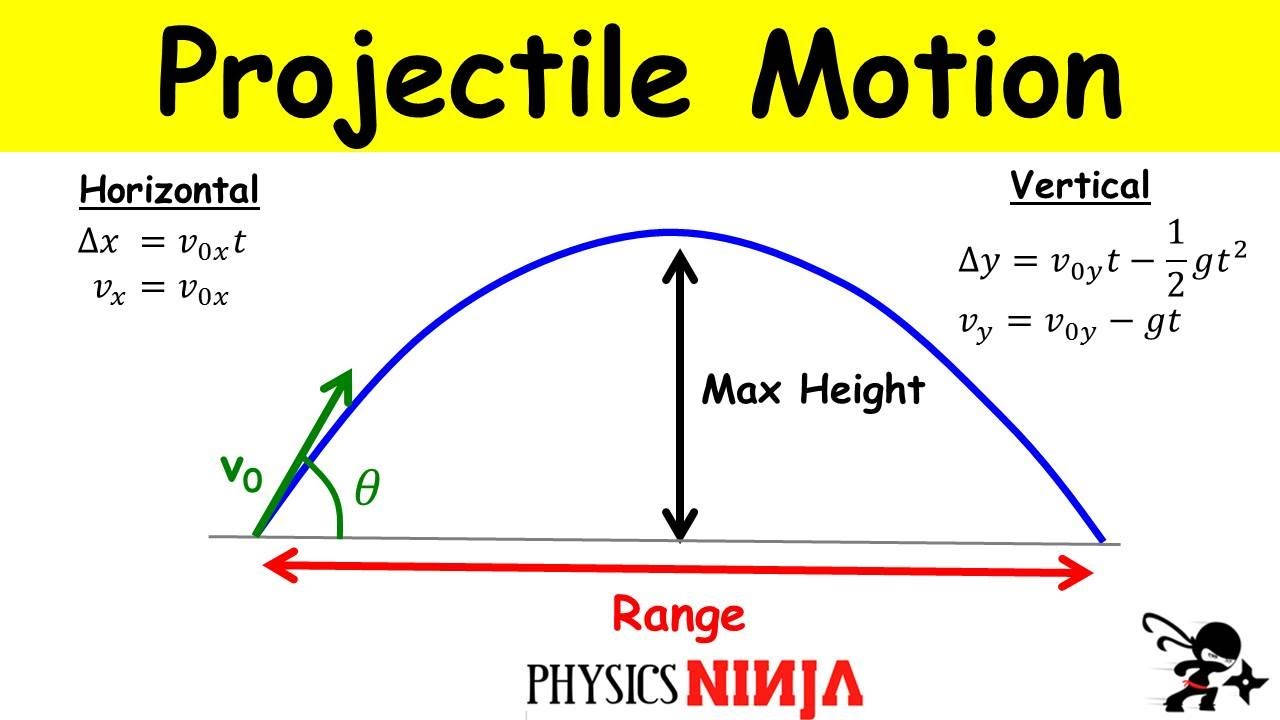
Projectile Motion: Finding the Maximum Height and the Range

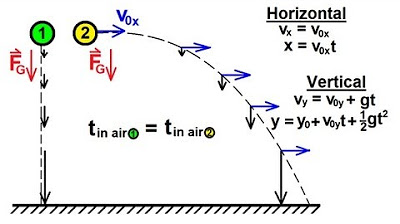
Physics 3: Motion in 2-D Projectile Motion (1 of 21) Independent Motion in x and y

Deriving the 6 Basic Projectile Motion Equations

Equations of Projectile Motion in Physics Explained - [1-4-6]

Why Does 45º Launch Angle Give Maximum Range? // HSC Physics

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Projectile MotionPhysics 1Kinematics2D MotionVelocity VectorAccelerationGravityConstant VelocityTrigonometrySymmetryTrajectory