Consolidation: Projectile Motion Calculations
TLDRThis video script delivers a concise guide on calculating projectile motion, emphasizing the importance of separating horizontal and vertical components. It explains how constant horizontal velocity and changing vertical velocity at 9.81 m/s^2 affect the motion, using a 5.2 m/s projectile launch as an example. The script outlines the process of resolving initial velocity, calculating landing speed through vertical motion, and determining the time of flight and horizontal distance. It also touches on maximum height and horizontal range calculations, offering multiple methods for determining the time of flight, and encouraging practice for mastery of the concept.
Takeaways
- 📌 In projectile motion, the horizontal component of velocity remains constant while the vertical component changes at a rate of 9.81 m/s^2 downward.
- 📏 To solve projectile motion problems, separate the horizontal and vertical components of motion and analyze them independently.
- 🌟 For a given projectile motion, the initial velocity can be resolved into horizontal (3.3 m/s) and vertical (3.98 m/s) components using trigonometric functions.
- 🔄 The horizontal velocity remains unchanged throughout the motion, so the landing horizontal velocity is the same as the initial horizontal velocity.
- 🚀 The vertical motion is a constant acceleration motion (9.81 m/s^2 downward), which allows us to use kinematic equations like v^2 = u^2 + 2as to find the final vertical velocity.
- 📐 To find the landing speed, use the Pythagorean theorem to combine the horizontal and vertical components of velocity.
- 🔢 The direction of the landing velocity is found by calculating the tangent ratio of the vertical and horizontal components of velocity.
- 🕒 The time of flight in projectile motion is determined by the vertical motion, which can be found using the kinematic equation v = u + at.
- 🏞️ For horizontal projectile motion, the initial vertical velocity is zero, simplifying calculations as there's no upward motion.
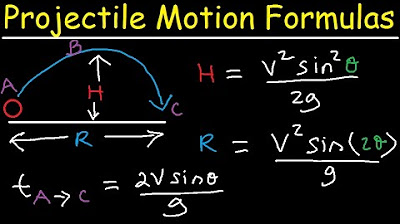
- 📈 The maximum height in projectile motion is reached when the vertical velocity is zero, which can be calculated using the kinematic equation v^2 = u^2 + 2as with v set to zero.
- 🏹 The horizontal range, or the distance the projectile travels before landing, can be calculated by multiplying the horizontal velocity by the time of flight.
Q & A
What is the key concept in solving projectile motion problems?
-The key concept in solving projectile motion problems is to separate the horizontal motion from the vertical motion, as they are independent of each other.
How does the horizontal component of velocity change in projectile motion?
-In projectile motion, the horizontal component of velocity remains constant throughout the motion because there is no horizontal acceleration acting on the object.
What is the formula used to link velocities and displacements in vertical motion?
-The formula used to link velocities and displacements in vertical motion is v² = u² + 2as, where v is the final velocity, u is the initial velocity, a is the acceleration, and s is the displacement.
How do you calculate the time of flight in projectile motion?
-The time of flight in projectile motion is determined by the vertical motion. It can be calculated using the formula s = ut + 0.5at² (for constant speed motion) or by using the quadratic formula to solve for time in the displacement-time formula s = v₀t + 0.5at².
What is the significance of the tangent ratio in determining the angle of the velocity vector in projectile motion?
-The tangent ratio is used to determine the angle of the velocity vector because it is the ratio of the vertical component of velocity to the horizontal component. The angle can be found using the arctangent function, which gives the angle whose tangent is the ratio of the vertical and horizontal components of velocity.
How does the initial velocity affect the horizontal and vertical components in projectile motion?
-The initial velocity is resolved into its horizontal and vertical components using trigonometric functions. The horizontal component (Vx) is given by the initial velocity multiplied by the cosine of the angle (Vx = V₀cosθ), and the vertical component (Vy) is given by the initial velocity multiplied by the sine of the angle (Vy = V₀sinθ).
What is the maximum height reached by a projectile in motion?
-The maximum height reached by a projectile is determined when the vertical velocity becomes zero, as this indicates the peak of the trajectory. It can be calculated using the formula h = (Vy²) / (2g), where Vy is the initial vertical velocity and g is the acceleration due to gravity.
How do you calculate the horizontal distance traveled by a projectile?
-The horizontal distance traveled by a projectile is calculated by multiplying the horizontal velocity by the time of flight. The horizontal velocity remains constant, so once the time of flight is known, the distance can be easily calculated.
What are the three methods mentioned in the script to calculate the time of flight for a projectile?
-The three methods are: 1) Using the VT equation at the peak of the trajectory where the vertical velocity is zero. 2) Recognizing the symmetry of the parabolic path and using the VT equation to find the time it takes to return to the initial vertical level. 3) Using the ST equation with the final vertical displacement being zero and solving for time.
What is the significance of the horizontal range in projectile motion?
-The horizontal range is the distance a projectile travels in the horizontal direction before it lands. It is significant as it determines how far the object will travel, which is a common parameter of interest in various applications of projectile motion.
How can the final velocity of a projectile be calculated?
-The final velocity of a projectile can be calculated by using the Pythagorean theorem to combine the constant horizontal velocity and the calculated vertical velocity at the moment of landing. The resultant velocity is found by taking the square root of the sum of the squares of the horizontal and vertical components.
Outlines
🚀 Understanding Projectile Motion
This paragraph introduces the concept of projectile motion, emphasizing that while the overall velocity changes, the horizontal component remains constant. It explains that the key to solving projectile motion problems is to separate the horizontal and vertical components of motion. A typical problem is presented, where an object is projected at a certain speed and angle. The initial velocity is resolved into its horizontal and vertical components, and the horizontal velocity is identified as constant throughout the motion. The focus is on calculating the final speed upon landing by considering only the vertical component of velocity and using the appropriate kinematic equations.
🎯 Calculating Landing Speed and Direction
The paragraph delves into the process of calculating the speed and direction at which a projectile lands. It explains how to use the Pythagorean theorem to find the resultant speed by considering the constant horizontal velocity and the calculated vertical velocity at landing. The direction is determined by the tangent ratio of the vertical and horizontal velocities. The paragraph also discusses how to calculate the horizontal distance traveled by considering the time of flight, which is determined by the vertical motion. Different methods for calculating the time of flight are introduced, including the use of symmetry in the projectile's path and the vertical displacement.
📈 Solving Special Projectile Motion Scenarios
This paragraph addresses special cases of projectile motion, such as horizontally launched projectiles, which simplify the calculations due to the initial vertical velocity being zero. The process of calculating the landing speed, angle, and horizontal distance for these scenarios is explained. The paragraph also covers how to determine the maximum height reached by the projectile by setting the final vertical velocity to zero and solving the kinematic equation. Various methods for calculating the time of flight and horizontal range are presented, highlighting the importance of understanding the separate horizontal and vertical motions in projectile problems.
Mindmap
Keywords
💡Projectile Motion
💡Horizontal Component
💡Vertical Component
💡Velocity
💡Acceleration
💡Time of Flight
💡Horizontal Range
💡Maximum Height
💡Kinematic Equations
💡Trigonometric Functions
Highlights
The key to solving projectile motion is to separate the horizontal motion from the vertical motion.
In projectile motion, the horizontal component of velocity remains constant while the vertical component changes at a rate of 9.81 m/s^2 downward.
To calculate the speed at which an object lands, one must resolve the initial velocity into its horizontal and vertical components.
The horizontal velocity remains constant throughout the motion, even when the object lands.
The vertical component of velocity at landing can be found using the formula v^2 = u^2 + 2as, where a is the acceleration due to gravity (9.81 m/s^2).
The speed of the projectile is calculated using the Pythagorean theorem, combining the horizontal and vertical components of velocity.
The direction of the projectile's velocity at landing can be determined using the tangent ratio, which is the vertical component divided by the horizontal component.
The horizontal distance traveled by the projectile can be calculated by multiplying the horizontal velocity by the time of flight.
The time of flight is determined by the vertical motion, specifically using the vertical displacement and the acceleration due to gravity.
At the maximum height of the projectile's trajectory, the vertical velocity is zero, while the horizontal velocity remains constant.
Projectiles launched horizontally have an initial vertical velocity of zero, simplifying calculations as there is no upward motion.
The landing speed for a horizontally launched projectile can be found by calculating the final vertical velocity and using the Pythagorean theorem.
The horizontal range, or the distance traveled before landing, is determined by the horizontal velocity and the time of flight.
Three methods to calculate the time of flight include using the VT equation at the peak, recognizing the symmetry of the parabolic path, and using the ST equation with the final vertical displacement being zero.
Understanding and applying the concepts of projectile motion allows for accurate predictions of an object's final velocity, angle, horizontal distance, and maximum height.
Practicing these calculations reinforces the understanding of projectile motion and its applications.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: