How To Solve Any Projectile Motion Problem (The Toolbox Method)
TLDRIn this educational video, Jesse Mason tackles a classic projectile motion problem, involving an angled launch from a cliff. The task is to calculate the projectile's range, peak height, and velocity at a specific time. Mason methodically identifies knowns and unknowns, sets up a coordinate system, and applies kinematic equations to both horizontal and vertical components of the motion. Through step-by-step calculations, he determines the projectile's horizontal displacement upon impact (160.1 meters), peak height (105.4 meters), and velocity two seconds after launch (29.70 meters per second at 18.3 degrees below horizontal). The video emphasizes the importance of creating a 'toolbox' of equations to dissect and solve complex motion problems.
Takeaways
- 📐 The problem involves a projectile launched at an angle from a cliff, with the goal to find the range, peak height, and velocity at a specific time.
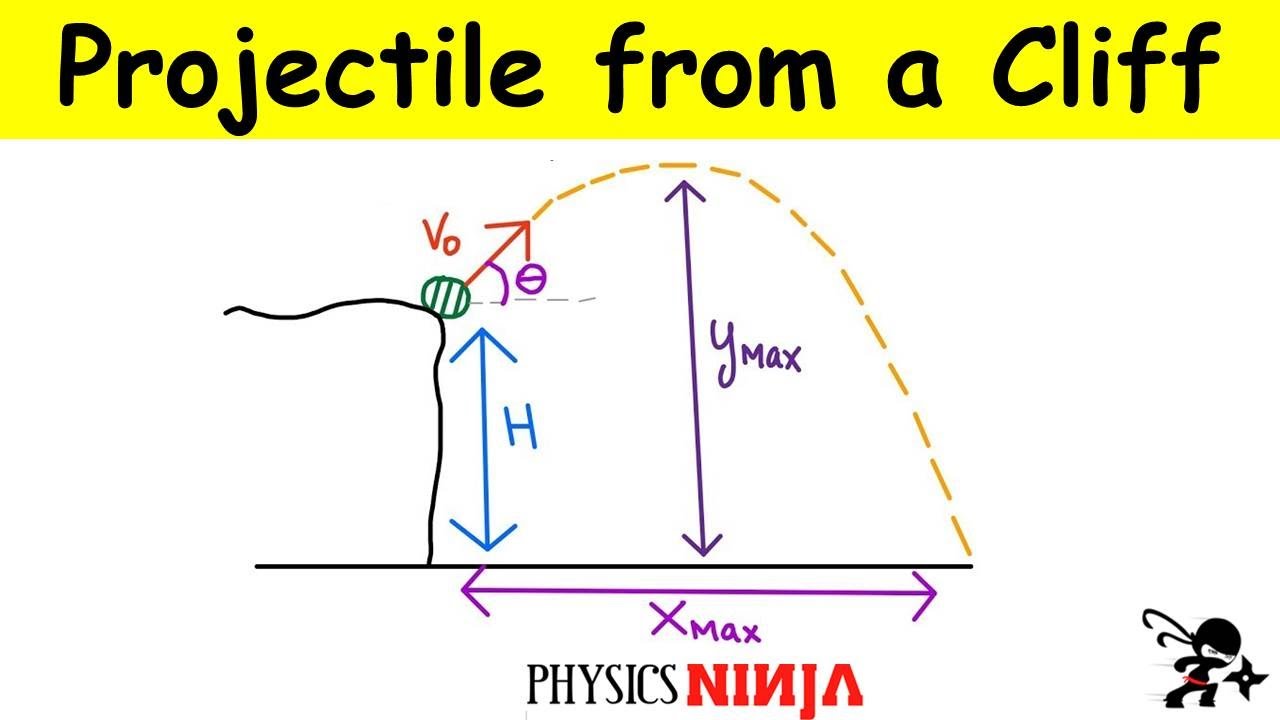
- 🏞️ Initial conditions given include a cliff height of 100 meters, a launch velocity of 30 m/s at an angle of 20 degrees above the horizontal.
- 🎨 A visual representation is essential, including the cliff, cannon, trajectory, and coordinate system aligned with the problem.
- 📌 Knowns include the initial vertical displacement (100m), launch velocity (30 m/s), launch angle (20°), and the acceleration due to gravity (-9.8 m/s²).
- 🎯 The unknowns are the projectile's horizontal range (x), maximum vertical displacement (y-max), and velocity components at a given time (2 seconds after launch).
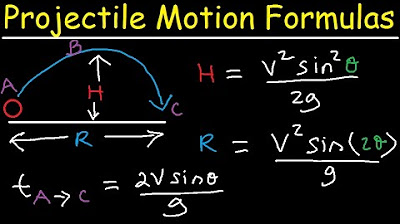
- 📑 The kinematic equations for projectile motion are applied separately to the horizontal (x) and vertical (y) components of motion.
- 🕒 Time of impact is determined by setting the vertical displacement to zero in the displacement equation (y = 0).
- 🏔️ The range (x) is calculated using the horizontal displacement equation with the time of impact (5.68 s), resulting in 160.1 meters.
- 🌄 The peak height (y-max) is found by inserting the time when the vertical velocity is zero (1.05 s) into the displacement equation, yielding 105.4 meters.
- 🚀 The velocity components at 2 seconds after launch are calculated using the velocity equations, resulting in 28.19 m/s horizontally and -9.34 m/s vertically.
- 📐 The magnitude of the velocity at 2 seconds is 29.70 m/s, and its direction is 18.3 degrees below the horizontal, determined using trigonometry.
Q & A
What is the main topic of the video?
-The main topic of the video is solving a classic projectile motion problem involving an angled launch from uneven ground.
What are the knowns in the projectile motion problem?
-The knowns are the initial vertical displacement (height of the cliff, 100 meters), the magnitude of the launch velocity (30 m/s), the launch angle (theta, 20 degrees), and the acceleration due to gravity (g, -9.8 m/s^2).
What are the unknowns the video aims to determine?
-The unknowns are the projectile's range (horizontal displacement upon impact), peak height (maximum vertical displacement), and velocity at a specific time (2 seconds after launch).
How is the acceleration due to gravity treated in the equations?
-The acceleration due to gravity is treated as a negative value (-9.8 m/s^2) because its direction is downward, opposite to the positive y-axis direction in the chosen coordinate system.
What are the kinematic equations used to analyze the projectile's motion?
-The kinematic equations used are the displacement equation and the velocity equation, applied separately to the horizontal (x) and vertical (y) directions.
How is the time of impact determined?
-The time of impact is determined by setting the vertical displacement (y) to zero in the displacement equation and solving for time (t).
What is the horizontal displacement (range) of the projectile upon impact?
-The horizontal displacement (range) of the projectile upon impact is 160.1 meters.
What is the maximum vertical displacement (peak height) of the projectile?
-The maximum vertical displacement (peak height) of the projectile is 105.4 meters.
What are the x- and y-components of the projectile's velocity 2 seconds after launch?
-The x-component of the velocity is 28.19 m/s and the y-component is -9.34 m/s (downward).
What is the magnitude and direction of the projectile's velocity 2 seconds after launch?
-The magnitude of the projectile's velocity 2 seconds after launch is 29.70 m/s, and its direction is 18.3 degrees below the horizontal.
How does the video emphasize the importance of creating a toolbox for solving problems?
-The video emphasizes that creating a toolbox, which refers to simplifying and selecting the appropriate displacement and velocity equations for each direction, is essential for effectively solving projectile motion problems.
Outlines
🚀 Introduction to Projectile Motion Problem
The video begins with Jesse Mason introducing a classic projectile motion problem involving an angled launch from uneven ground. The problem requires determining the projectile's range, peak height, and velocity at a specific time. Jesse emphasizes the importance of visualizing the problem by drawing a picture, which includes a cliff, level ground, and the cannon's initial position. Known quantities include the cliff's height (100 meters), the projectile's launch velocity (30 m/s), and the launch angle (20 degrees). The unknowns are the projectile's range (x), peak height (y-max), and velocity components at a later time (v-sub-x and v-sub-y). Jesse also discusses the coordinate system and the acceleration due to gravity (g = -9.8 m/s^2), and how they will be used in the calculations.
📚解析运动方程
In this paragraph, Jesse Mason continues to dissect the projectile motion problem by breaking down the motion into its horizontal and vertical components. He simplifies the kinematic equations for both directions, considering the projectile's horizontal motion as unaccelerated and the vertical motion affected by gravity. The horizontal displacement equation simplifies to x = v-sub-oh cosine theta t, and the horizontal velocity equation to v-sub-x = v-sub-oh cosine theta. For the vertical motion, the displacement equation becomes y = (1/2) g t^2 + v-sub-oh sine theta t + y-sub-oh, and the vertical velocity equation to v-sub-y = v-sub-oh sine theta + g t. These equations form the 'toolbox' for solving the projectile motion problem.
🎯 Solving for Range, Peak Height, and Velocity
Jesse Mason concludes the video by solving the projectile motion problem using the previously established equations. He first calculates the projectile's range (x) by using the time of impact (t) derived from the vertical displacement equation (y = 0), which gives a time of 5.68 seconds and a range of 160.1 meters. Next, he determines the peak height (y-max) by finding the time when the vertical velocity is zero (t = 1.05 seconds), resulting in a peak height of 105.4 meters. Lastly, he calculates the projectile's velocity components 2 seconds after launch, obtaining a horizontal component of 28.19 m/s and a vertical component of -9.34 m/s. By combining these components, he finds the magnitude of the velocity to be 29.70 m/s and the direction to be 18.3 degrees below the horizontal. Jesse wraps up by emphasizing the importance of creating a 'toolbox' for solving such problems and invites viewers to suggest topics for future videos.
Mindmap
Keywords
💡Projectile Motion
💡Initial Position and Velocity
💡Range
💡Peak Height
💡Velocity Components
💡Acceleration Due to Gravity (g)
💡Kinematic Equations
💡Trigonometry
💡Coordinate System
💡Time of Impact
💡Velocity Vector
Highlights
The problem involves analyzing projectile motion with an angled launch from uneven ground.
The initial position and velocity of the projectile are given to determine its range, peak height, and velocity at a point in its trajectory.
The height of the cliff is 100 meters, representing the initial vertical displacement.
The launch velocity magnitude is 30 meters per second at an angle of 20 degrees.
The unknowns include the projectile's horizontal displacement (range), maximum vertical displacement (peak height), and velocity components after 2 seconds.
The acceleration due to gravity (g) is considered negative (-9.8 m/s^2) in the chosen coordinate system.
Kinematic equations are applied separately to the horizontal (x) and vertical (y) directions to analyze the projectile's motion.
The horizontal displacement equation simplifies to x = v0*cos(theta)*t, ignoring horizontal acceleration.
The vertical displacement equation is y = 0.5*g*t^2 + v0*sin(theta)*t + y0, with y0 being the initial vertical displacement.
The time of impact is found by setting the vertical displacement to zero and solving the vertical displacement equation.
The projectile's range is calculated to be 160.1 meters using the horizontal displacement equation with the time of impact.
The peak height is determined to be 105.4 meters by finding the time when the vertical velocity component is zero.
The velocity components 2 seconds after launch are calculated as 28.19 m/s horizontally and -9.34 m/s vertically.
The magnitude of the velocity vector 2 seconds after launch is 29.70 m/s, found using Pythagoras' Theorem.
The direction of the velocity vector 2 seconds after launch is 18.3 degrees below the horizontal, calculated using trigonometry.
The video emphasizes the importance of creating a 'toolbox' of equations to solve projectile motion problems effectively.
The presenter, Jesse Mason, invites viewers to suggest topics for future 'Teach Me' videos and to engage in the comments section.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: