Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (90 of 92) A High Energy Proton

Michel van Biezen
19 May 201806:27
EducationalLearning
32 Likes 10 Comments

TLDRThe lecture explores the probability of a 20 MeV proton penetrating a high potential barrier of varying widths, from 1 to 5 femtometers. The transmission coefficient calculations reveal that the probability drops dramatically as the barrier width increases, with the chance of passing through falling from 0.56 for a 1 femtometer barrier to less than 1 in a million for a 5 femtometer barrier. This illustrates the rapid diminishment of a particle's likelihood to traverse a widening barrier.

Takeaways
  • πŸ”¬ A 20 MeV proton is attempting to pass through a barrier with a potential of 40 MeV.
  • 🧬 The barrier widths vary from 1 to 5 femtometers, which is in the order of the radius of a nucleus.
  • πŸš€ The transmission coefficient (probability) of the proton passing through the barrier is calculated using the formula T = 4 * e^(-2Ξ±L), where Ξ± is a large number due to the proton's mass and energy.
  • πŸ“‰ The probability of the proton passing through the barrier decreases exponentially as the barrier width increases.
  • 🌟 For a 1 femtometer wide barrier, the probability is approximately 0.56, which is slightly over 1/2.
  • πŸ“‰ When the barrier width doubles to 2 femtometers, the probability drops to 0.08.
  • πŸ“‰ At 3 femtometers, the probability further decreases to about 0.01 or 1%.
  • πŸ“‰ For a 4 femtometer barrier, the probability drops to less than one in a million.
  • πŸ“‰ At the 5 femtometer width, the probability is extremely small, approximately 2.2 * 10^(-4).
  • πŸ’‘ The alpha value is crucial in determining the transmission probability, with a higher alpha leading to a higher initial probability.
  • 🌐 The concept demonstrates the quantum tunneling effect and how it diminishes with increasing barrier widths and insufficient energy.
Q & A

  • What is the energy level of the proton mentioned in the lecture?

    -The proton has an energy level of 20 MeV (million electron volts).

  • What is the potential barrier the proton is trying to pass through?

    -The proton is trying to pass through a barrier with a potential of 40 MeV (million electron volts).

  • What is the range of widths for the barrier being considered?

    -The barrier widths considered range from 1 femtometer to 5 femtometers, which is in the order of the radius of a nucleus.

  • How does the width of the barrier affect the probability of the proton passing through?

    -As the width of the barrier increases, the probability of the proton passing through decreases drastically.

  • What is the calculated transmission coefficient (probability) for the proton passing through a 1 femtometer wide barrier?

    -The transmission coefficient for a 1 femtometer wide barrier is approximately 0.56 or 56%.

  • What is the transmission coefficient for the proton passing through a 2 femtometer wide barrier?

    -The transmission coefficient for a 2 femtometer wide barrier is 0.08 or 8%.

  • What is the formula used to calculate the transmission coefficient?

    -The formula used is T = 4 * e^(-2 * alpha * L), where T is the transmission coefficient, alpha is a constant, and L is the width of the barrier.

  • What is the value of alpha used in the calculations?

    -The value of alpha used in the calculations is 9.8 * 10^14.

  • How does the mass of the particle affect the transmission probability?

    -The mass of the particle affects the value of alpha, which in turn affects the transmission probability. A smaller mass, like that of an electron, results in a smaller alpha and thus a different rate of drop in transmission probability.

  • What happens to the probability as the width of the barrier increases beyond 1 femtometer?

    -The probability drops off very quickly as the width of the barrier increases beyond 1 femtometer, indicating that the proton is much less likely to pass through wider barriers.

  • What is the transmission coefficient for the proton passing through a 5 femtometer wide barrier?

    -The transmission coefficient for a 5 femtometer wide barrier is approximately 2.2 * 10^(-4) or 0.00022, which is a very small probability.

Outlines
00:00
πŸ”¬ Quantum Tunneling and Barrier Penetration

This paragraph discusses a theoretical scenario where a high-energy proton with 20 MeV is attempting to pass through a barrier with varying widths, starting from 1 femtometer to 5 femtometers, which is in the order of the radius of a nucleus. The barrier's potential is much higher than the proton's energy, set at 40 MeV. The lecture introduces the concept of alpha, a large number representing the ratio of the proton's mass and energy, which is calculated to be 9.8 x 10^14. The transmission coefficient, representing the probability of the proton getting through the barrier, is derived and calculated for each width of the barrier. It is shown that as the barrier width increases, the probability of the proton passing through decreases exponentially, with a significant drop from 0.56 for a 1 femtometer barrier to 0.01 (1%) for a 3 femtometer barrier, and further diminishing to less than one in a million for a 5 femtometer barrier. This illustrates the rapid decrease in the likelihood of quantum tunneling as the barrier width increases.

05:00
🧠 Re-evaluating Quantum Tunneling Probabilities

The speaker acknowledges a potential mistake in the previous calculation and revisits the quantum tunneling probabilities for a proton passing through a barrier of varying widths. The focus is on correcting the calculation for the probability when the barrier width is 5 femtometers. The corrected probability is found to be 2.2 x 10^-4, which is still very small but not as tiny as initially thought. The speaker emphasizes that the probability of a proton passing through a barrier drops to virtually zero as the barrier width increases significantly, providing insight into the behavior of quantum particles and the limitations of their energy in overcoming such barriers.

Mindmap
Keywords
πŸ’‘High-energy proton
A high-energy proton refers to a proton that has been accelerated to a high velocity, typically in a particle accelerator, and possesses significant kinetic energy. In the video, the high-energy proton is the subject of the experiment, attempting to pass through a high potential barrier. This concept is central to understanding the quantum tunneling phenomenon being discussed, as the proton's energy and interaction with the barrier determine the probability of it getting through.
πŸ’‘Quantum tunneling
Quantum tunneling is a quantum mechanical phenomenon where a particle can pass through a potential barrier that it classically shouldn't be able to overcome due to insufficient energy. In the video, the concept of quantum tunneling is central to the discussion of the proton's ability to pass through the high potential barrier despite the energy discrepancy.
πŸ’‘Potential barrier
A potential barrier is an energy barrier that a particle must overcome to move from one region to another. In the context of the video, the barrier is described as having a very high potential, which means it requires a significant amount of energy for a particle to cross. The barrier's width and height (in terms of energy) are crucial factors in determining the probability of quantum tunneling.
πŸ’‘Femtometer
A femtometer (fm) is a unit of length in the metric system, equal to one quadrillionth of a meter (10^-15 meters). In the video, femtometers are used to describe the width of the potential barrier, which is varied from 1 fm to 5 fm to study the effect of barrier width on the probability of the proton passing through.
πŸ’‘Transmission coefficient
The transmission coefficient, in the context of quantum mechanics, represents the probability that a particle will tunnel through a potential barrier. It is a crucial concept in the video as it quantifies the likelihood of the high-energy proton successfully passing through the barrier.
πŸ’‘Alpha (Ξ±)
In the context of the video, Alpha (Ξ±) is a constant used in the calculation of the transmission coefficient for quantum tunneling. It is related to the mass and energy of the particle, and its value is used to determine the probability of the particle passing through the barrier.
πŸ’‘Electronvolt (eV)
An electronvolt (eV) is a unit of energy that is commonly used in the field of particle physics. It represents the amount of kinetic energy gained or lost by an electron when it passes through an electric potential difference of one volt. In the video, the energy of the proton is given in million electronvolts (MeV), which is a significant amount of energy that influences the quantum tunneling process.
πŸ’‘Conversion to joules
The process of converting energy from electronvolts to joules is necessary to use in the calculations involving quantum mechanics, as the standard unit of energy in the International System of Units (SI) is the joule. In the video, the conversion from MeV to joules is implied when discussing the energy of the proton and the potential barrier.
πŸ’‘H-bar (Δ§)
H-bar (Δ§), also known as the reduced Planck constant, is a fundamental constant in quantum mechanics. It is half of the Planck constant divided by 2Ο€ (h/2Ο€). It appears in the formulas for quantum tunneling and is used to relate the energy and momentum of particles to observable quantities. In the video, H-bar is part of the formula for calculating the transmission coefficient.
πŸ’‘Exponential function
The exponential function is a mathematical function that describes growth or decay at a constant rate. In quantum mechanics, it is used to calculate the probability of quantum tunneling, where the function e to the power of a negative number represents the decay of the wave function as it encounters the potential barrier.
πŸ’‘Probability
In the context of the video, probability refers to the likelihood of the high-energy proton successfully tunneling through the potential barrier. The script calculates this probability for different barrier widths, demonstrating how the width of the barrier significantly affects the outcome.
Highlights

A high-energy proton is attempting to pass through a barrier with high potential.

The proton has an energy of 20 MeV (million electron volts).

The barrier's potential is 40 MeV, significantly higher than the proton's energy.

The barrier widths vary from 1 to 5 femtometers, comparable to the radius of a nucleus.

The transmission coefficient (probability) of the proton passing through the barrier is calculated using a specific formula.

The alpha value, a significant factor in the calculation, is found to be 9.8 x 10^14.

As the barrier width increases, the probability of the proton passing through decreases exponentially.

For a barrier width of 1 femtometer, the probability is 0.56, slightly over 1/2.

Doubling the barrier width to 2 femtometers reduces the probability to 0.08.

At a barrier width of 3 femtometers, the probability drops to approximately 0.01%.

For a 4 femtometer barrier, the probability is less than one in a million.

At the widest barrier of 5 femtometers, the probability is calculated to be 2.2 x 10^-4.

The mass and energy of the proton play a crucial role in its ability to pass through the barrier.

An electron would have a much higher probability due to its smaller mass and larger alpha.

The lecture provides a clear demonstration of quantum tunneling and its dependence on particle mass and barrier width.

The rapid decrease in probability with increasing barrier width illustrates the sensitivity of quantum phenomena to physical dimensions.

The lecture's calculations and findings are valuable for understanding the behavior of particles at the quantum level.

Transcripts

Browse More Related Video

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (89 of 92) Which Penetrates Easier?

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (78 of 92) The Barrier: Amplitude

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (79 of 92) Simplified Transmission Coeff.

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (62 of 92) Transmission vs Reflection

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (76 of 92) Penetration Depth V0, E: Ex.

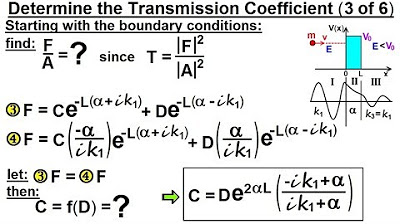
Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (85 of 92) Transmission Coeff=? (3 of 6)

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Quantum MechanicsParticle PhysicsTunneling EffectHigh Energy PhysicsProton BarrierProbability CalculationNuclear RadiusQuantum BarriersPhysics LectureEducational Content