Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (89 of 92) Which Penetrates Easier?

Michel van Biezen
18 May 201808:42
EducationalLearning
32 Likes 10 Comments

TLDRThe video script explores the transmission coefficient and the probability of particles, specifically electrons and protons, passing through a barrier. It compares the two scenarios where both particles have the same energy but different masses, resulting in different probabilities of passing the barrier. The script explains that due to its larger mass, a proton has a smaller chance of getting through the barrier compared to an electron. The mathematical calculations provided illustrate this concept, showing that while 15.7% of electrons might pass through, virtually no protons would, highlighting the impact of particle mass on the likelihood of barrier penetration.

Takeaways
  • 🌟 The transmission coefficient and probability of a particle passing through a barrier are central concepts in quantum mechanics.
  • 🔬 In a comparison between an electron and a proton with the same energy of 10 electron volts facing a 20 electron volt barrier, the proton's chances are significantly lower due to its greater mass.
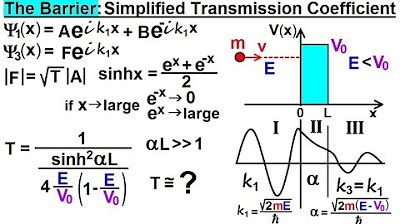
  • 📉 The simplified transmission coefficient (T) can be approximated as T ≈ e^(-2αL), where α is the exponential decay constant and L is the barrier width.
  • 🎯 α is calculated based on the formula α = √(2 * m * (V - E) / ħ), with m being the particle mass, V the barrier potential, E the particle energy, and ħ the reduced Planck constant.
  • 🚀 For the proton, α is much larger due to its greater mass, leading to a smaller transmission coefficient and virtually zero probability of passing the barrier.
  • 🌐 For the electron, a smaller α results in a larger transmission coefficient, indicating a 15.7% chance of passing through the barrier.
  • 🔄 The barrier width (L) is a fixed number, and the main factor affecting the transmission coefficient is the particle's mass.
  • 🤔 Larger particles, like alpha or beta particles in nuclear decay, require a higher energy to overcome the potential barrier and escape the nucleus.
  • 💡 The difference in transmission probabilities highlights the particle's wave-like behavior in quantum mechanics, where smaller particles have a higher likelihood of tunneling through barriers.
  • 🧠 Understanding these concepts is crucial for grasping nuclear decay processes and the behavior of particles in quantum states.
Q & A

  • What is the main topic of the transcript?

    -The main topic of the transcript is the conceptual understanding of the transmission coefficient and the probability of a particle, specifically an electron and a proton, making it through a barrier with the same energy.

  • What are the key factors affecting the transmission coefficient?

    -The key factors affecting the transmission coefficient are the energy of the particles, the potential of the barrier, the width of the barrier, and the mass of the particle.

  • How does the mass of a particle influence its probability of passing through a barrier?

    -The mass of a particle significantly influences its probability of passing through a barrier. A heavier particle, like a proton, will have a larger exponential decay constant (alpha), resulting in a smaller transmission coefficient and thus a lower probability of passing through the barrier compared to a lighter particle like an electron.

  • What is the role of the exponential decay constant (alpha) in determining the transmission coefficient?

    -The exponential decay constant (alpha) describes how the probability of a particle passing through a barrier declines as the barrier widens. A larger alpha results in a smaller transmission coefficient, indicating a lower probability of passage.

  • How is the potential barrier's width represented in the transmission coefficient formula?

    -The potential barrier's width is represented as 'L' in the transmission coefficient formula, and it is a fixed number for a particular example. The wider the barrier, the smaller the probability of a particle passing through it.

  • What is the significance of the transmission coefficient in the context of nuclear decay?

    -In the context of nuclear decay, the transmission coefficient is significant because it helps to determine how large particles, such as alpha or beta particles, can escape the nucleus. These particles need to have a very large energy to overcome the potential barrier and decay.

  • What happens to particles with energies insufficient to pass through the barrier?

    -Particles with energies insufficient to pass through the barrier will be reflected off the barrier, or they may stop because their energy doesn't make it all the way through, resulting in partial penetration or no penetration at all.

  • How does the wavelength of a particle relate to its mass and the probability of passing through a barrier?

    -A particle with a larger mass has a smaller wavelength, which makes it less likely to pass through a barrier due to the increased probability of interactions with the barrier's potential field.

  • What is the numerical value of the transmission coefficient for a proton with the given conditions?

    -The numerical value of the transmission coefficient for a proton with the given conditions (10 eV energy, 20 eV barrier potential, and 100 picometers barrier width) is approximately equal to zero, indicating a very low probability of passing through the barrier.

  • What is the numerical value of the transmission coefficient for an electron under the same conditions?

    -The numerical value of the transmission coefficient for an electron under the same conditions is approximately 0.157, or 15.7%, indicating a much higher probability of passing through the barrier compared to a proton.

  • How can the principles discussed in the transcript be applied to understanding particle behavior in quantum mechanics?

    -The principles discussed in the transcript, such as the transmission coefficient and the effects of mass and energy on particle behavior, are fundamental to understanding quantum tunneling and the probabilistic nature of particle behavior in quantum mechanics.

Outlines
00:00
🔬 Quantum Mechanics: Electron vs Proton Barrier Transmission

This paragraph discusses the transmission coefficient and the probability of a particle, specifically an electron and a proton with the same energy, passing through a barrier. It introduces a simplified version of the transmission coefficient formula, highlighting the significance of the exponential decay constant (alpha) and how it varies with the mass of the particle. The comparison between the electron and proton's ability to pass through a barrier with a potential of 20 electron volts is made, emphasizing that the proton, having a larger mass, has a smaller transmission coefficient and thus a lower probability of making it through the barrier.

05:02
🌟 Particle Behavior in Nuclear Decay: Barrier Penetration

The second paragraph delves into the behavior of large particles during nuclear decay, explaining that they must overcome a potential barrier to be emitted from the nucleus. It contrasts the transmission probabilities of small and large particles, noting that smaller particles like electrons have a higher chance of penetrating the barrier, while larger particles such as protons require significantly more energy. The paragraph concludes by mentioning that future videos will provide examples of alpha and beta particles overcoming barriers, which is crucial for understanding nuclear decay processes.

Mindmap
Keywords
💡Transmission Coefficient
The transmission coefficient is a quantitative measure used in quantum mechanics to describe the probability of a particle passing through a potential barrier. In the context of the video, it is used to compare the likelihood of an electron versus a proton with the same energy getting through a barrier. The script explains that the transmission coefficient is influenced by the mass of the particle, with heavier particles like protons having a lower probability of transmission due to their larger mass and smaller wavelength.
💡Electron Volts
An electron volt (eV) is a unit of energy that is commonly used in the fields of physics and chemistry, particularly in the context of atomic and subatomic processes. It represents the amount of kinetic energy gained or lost by a single electron when it passes through an electric potential difference of one volt. In the video, the energy of both the electron and proton is specified as 10 electron volts, which is used as a basis for comparing their transmission coefficients through a barrier.
💡Barrier
In the context of the video, a barrier refers to a region in space where a particle must overcome a potential energy difference to pass through. This is analogous to a physical barrier but on a quantum scale. The properties of the barrier, such as its width (L) and potential (V), play a crucial role in determining the transmission coefficient and thus the probability of a particle getting through it.
💡Potential Energy
Potential energy is the energy an object possesses due to its position in a force field, such as an electric or gravitational field. In quantum mechanics, potential energy is often associated with the energy levels of particles in a potential well or barrier. The video discusses a potential barrier that particles must overcome to pass through, with the height of the barrier being described by the potential energy difference (V).
💡Mass
Mass is a fundamental property of matter that relates to the amount of matter in an object and its resistance to acceleration. In the context of the video, the mass of a particle is crucial in determining the transmission coefficient, as heavier particles like protons have a smaller probability of passing through a barrier due to their larger mass and the resulting smaller wavelength.
💡Exponential Decay Constant (Alpha)
The exponential decay constant, denoted as alpha (α), describes the rate at which the probability of a particle passing through a barrier decreases as the width of the barrier increases. It is directly related to the mass of the particle and is used in the calculation of the transmission coefficient. A larger alpha indicates a more rapid decrease in probability with increasing barrier width, which is the case for heavier particles like protons.
💡Wavelength
Wavelength is the spatial period of a wave, and in the context of quantum mechanics, it is related to the de Broglie hypothesis, which states that particles can exhibit wave-like properties. The wavelength of a particle is inversely proportional to its momentum, and thus, particles with greater mass have shorter wavelengths. In the video, the wavelength is implied to be smaller for the proton than for the electron due to the proton's greater mass, affecting its ability to pass through the barrier.
💡Quantum Tunneling
Quantum tunneling is a phenomenon in quantum mechanics where a particle can pass through a potential barrier that it classically could not overcome. This is due to the wave-like nature of particles, which allows for a non-zero probability of finding the particle on the other side of the barrier, even if it does not have enough energy to surmount the barrier classically. The video discusses the transmission coefficient, which is directly related to the probability of quantum tunneling occurring for particles like electrons and protons.
💡Probability
In the context of the video, probability refers to the likelihood of a particle successfully passing through a barrier. It is calculated using the transmission coefficient, which takes into account the properties of the barrier and the characteristics of the particle, such as its mass and energy. The video compares the probabilities for an electron and a proton to demonstrate how mass affects the likelihood of particles getting through a barrier.
💡Nuclear Decay
Nuclear decay is a process in which an unstable atomic nucleus loses energy by emitting radiation, such as alpha or beta particles. This process is significant in the video as it relates to the concept of particles overcoming potential barriers within the nucleus. The decay process often involves particles having to tunnel through a potential barrier within the nucleus, which is analogous to the quantum tunneling discussed in the context of the electron and proton example.
💡Reflection
In the context of the video, reflection refers to the phenomenon where particles, upon encountering a barrier, are turned back or bounce off rather than passing through. This is a classical outcome for particles that do not have enough energy to overcome a barrier or do not exhibit quantum tunneling. The video discusses that most particles will be reflected off the barrier, with only a small percentage having the ability to pass through due to quantum tunneling.
Highlights

The discussion compares the transmission of electrons and protons through a barrier with the same energy.

Both particles have an energy of 10 electron volts trying to pass through a 20 electron volt barrier.

The transmission coefficient is simplified for large alpha values, which is expected in this example.

The simplified transmission coefficient is approximately equal to e to the minus 2 alpha L, ignoring a small constant factor.

The alpha value is related to the mass of the particle; protons have a much larger alpha than electrons due to their greater mass.

A larger alpha results in a smaller transmission coefficient and thus a lower probability of passing through the barrier.

Protons are much less likely to pass through the barrier compared to electrons because of their larger mass and smaller wavelength.

The transmission coefficient for a proton is calculated to be almost zero, indicating very low probability.

For an electron, the transmission coefficient is significantly higher, with a 15.7% chance of passing through the barrier.

The example illustrates the impact of particle mass on the probability of quantum tunneling.

Larger particles require more energy to overcome the potential barrier in nuclear decay.

Alpha particles or beta particles need a large energy to penetrate the nuclear barrier.

The video aims to show examples of particles overcoming the nuclear barrier in future content.

The difference in transmission probability between protons and electrons demonstrates the principle of quantum tunneling.

Most particles will be reflected or stopped by the barrier, with only a small percentage making it through.

The content provides a conceptual understanding of the transmission coefficient and quantum tunneling probabilities.

Transcripts

Browse More Related Video

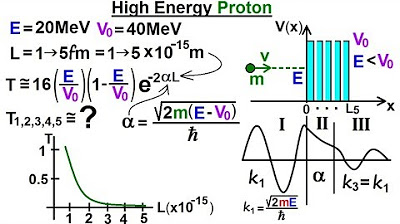
Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (90 of 92) A High Energy Proton

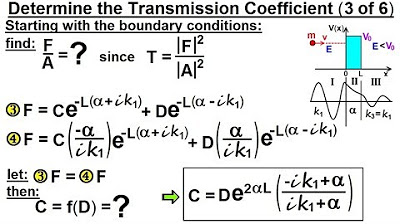
Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (85 of 92) Transmission Coeff=? (3 of 6)

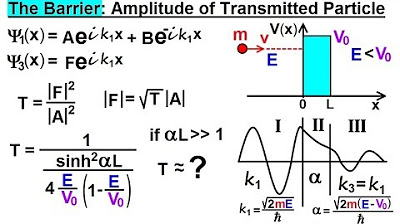
Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (78 of 92) The Barrier: Amplitude

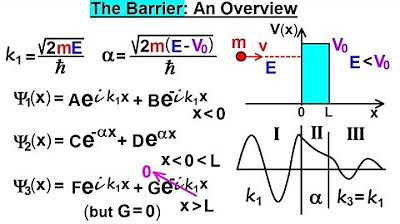
Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (77 of 92) The Barrier: An Overview

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (79 of 92) Simplified Transmission Coeff.

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (76 of 92) Penetration Depth V0, E: Ex.

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
QuantumMechanicsParticlePhysicsTransmissionCoefficientElectronVsProtonBarrierPenetrationEnergyComparisonQuantumTunnelingPhysicsEducationScientificComparisonEducationalContent