Least Common Multiple (LCM)

Professor Dave Explains

22 Aug 201705:40

EducationalLearning

32 Likes 10 Comments

TLDRThe script explains the concept of least common multiples, using basic multiplication tables and lists of multiples for numbers like 3, 4, and 5 as examples. It then explains how to find the least common multiple between two numbers, first by listing multiples and finding the smallest in common, and then using prime factorization as a shortcut for larger numbers. An application is finding least common denominators for fractions to more easily compare their sizes. Overall it aims to teach the importance of least common multiples.

Takeaways

😀 A multiple is a number that you get when you multiply a number by the positive integers.
😊 The least common multiple (LCM) of two numbers is the smallest number that is a multiple of both numbers.
😇 To find the LCM, write out the multiples of each number and look for the smallest number common to both lists.
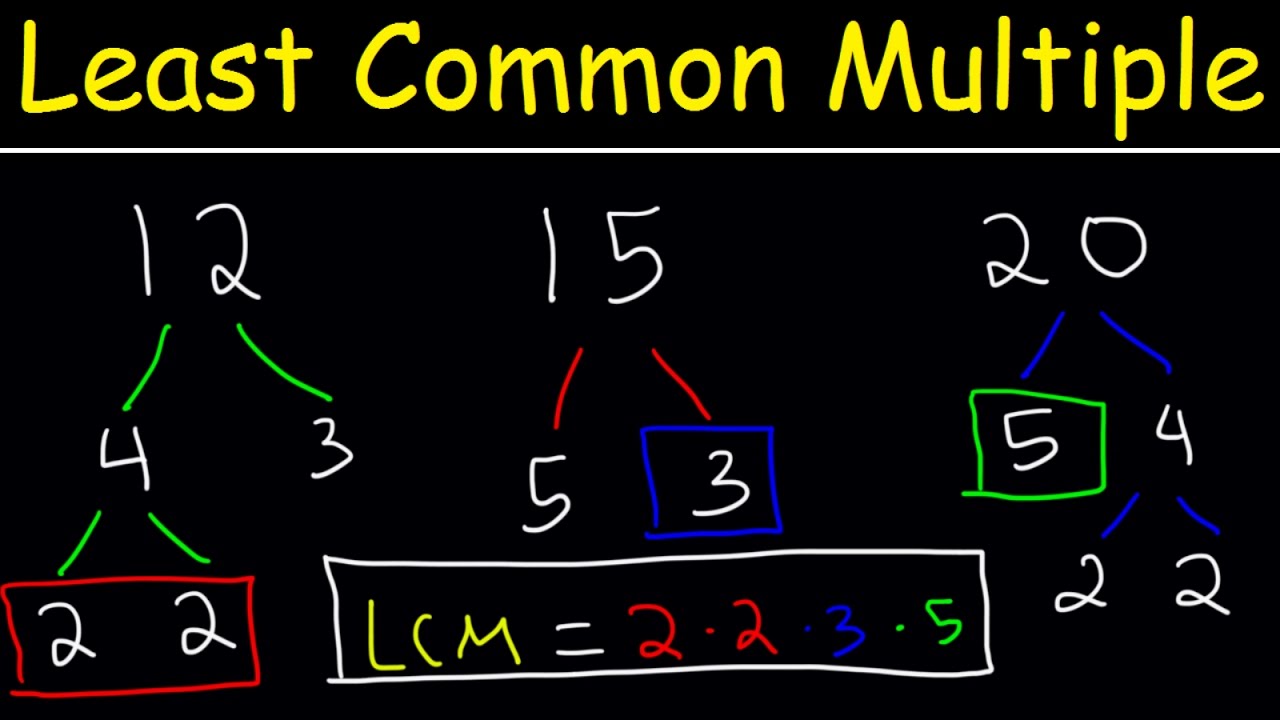
🤓 For bigger numbers, find the prime factorization and take the product of the prime factors, using the max number of times each factor appears.
🧐 The LCM of two numbers will always be a common multiple, but not always the smallest.
😎 The product of two numbers is always a common multiple, but not always the LCM.
🤔 To compare fractions with different denominators, convert them to equivalent fractions with the LCM as the denominator.
😣 Multiplying the numerator and denominator by the same number doesn't change the value of a fraction.
🥳 Using the LCM makes comparing the relative sizes of fractions easier when the denominators differ.
😉 Finding the LCM has applications in comparing fractions and solving other math problems.

Q & A

What is a multiple?
-A multiple is a number that you get when you multiply a number by all the positive integers. For example, multiples of 3 are 3, 6, 9, 12, etc.
How do you find the least common multiple of two numbers?
-To find the least common multiple, write out the multiples of both numbers and find the smallest number that is in both lists. You can also find the prime factorization of both numbers, take all the prime factors, and multiply them together using the greatest exponent for each.
When is simply multiplying two numbers together guaranteed to give you their least common multiple?
-Multiplying two numbers together will always give you a common multiple, because the product must have both original numbers as factors. However, this product may not always be the smallest or least common multiple.
Why write out multiples of small numbers to find their least common multiple?
-For smaller numbers, writing out the multiples is an easy way to visually identify the smallest number that is common to both lists. This becomes tedious for larger numbers.
What is the prime factorization method for finding least common multiples?
-Break down both numbers into their prime factors. Then take all the prime factors and multiply them together, using the greatest exponent that each factor appears. This will give you the least common multiple.
How can least common multiples help compare fractions?
-By finding a common denominator, you can rewrite two fractions so they have the same bottom number. This makes it easier to visually compare which fraction is larger based on the numerators.
What does it mean to alter a fraction without changing its value?
-You can multiply the numerator and denominator of a fraction by the same number without changing its quantitative value. The fraction will be expressed differently but will represent the same magnitude.
Why is one third larger than one fourth?
-When you find their least common multiple (12) and rewrite them (4/12 and 3/12), it becomes clear that 4 is bigger than 3, so 4/12 represents a larger fractional quantity than 3/12.
What are some real-world uses of least common multiples?
-Finding least common multiples is useful for comparing fractions, finding lowest common denominators, simplifying ratios, finding compatible intervals for time Keeping and scheduling, and other practical mathematical applications.
Can you rely on a common multiple always being the least common multiple?
-No, just because a number is a common multiple of two numbers does not guarantee it is the smallest or least common multiple. You need to check other multiples or use the prime factorization method.

Outlines

00:00

📚 Introducing Least Common Multiples

This paragraph introduces the concept of multiples and common multiples of numbers. It explains how to construct multiplication tables and compare the multiples of different numbers to find the smallest number that is common to both lists, called the least common multiple.

😀 Finding the Least Common Multiple

This paragraph provides examples of finding the least common multiple of number pairs like 3 and 5, 4 and 5, etc. It explains that sometimes the least common multiple is simply the product of the two numbers but not always. An example with 6 and 9 is shown where the least common multiple is 18, less than the product.

🧮 Shortcut Method for Bigger Numbers

For larger numbers, listing all multiples can get tedious. A shortcut method is introduced using prime factorization. The steps involve breaking down the numbers into prime factors, taking the highest power of each prime factor, and multiplying those together to directly reach the least common multiple.

📏 Applying Least Common Multiples to Fractions

An application of least common multiples is comparing fractions with different denominators. By finding a common denominator using the least common multiple technique, fractions can be expressed in an equivalent form to easily assess their relative magnitudes.

🧠 Checking Comprehension

The final paragraph indicates it is now time to check comprehension of the concepts covered in the video.

Mindmap

Keywords

💡multiple

A multiple is a number that you get when you multiply a given number by the positive integers. For example, multiples of 3 are 3, 6, 9, 12, etc. Understanding multiples is key to finding the least common multiple between two numbers. The video explains how to write out multiples and use them to identify the smallest number that is a multiple of both original numbers.

💡least common multiple

The least common multiple between two numbers is the smallest number that is a multiple of both numbers. This concept is important for comparing fractions with different denominators. By finding a common denominator, you can express the fractions with the same denominator and more easily compare their magnitudes.

💡prime factorization

The prime factorization of a number involves expressing it as a product of prime factors. This method provides a shortcut for finding the least common multiple between larger numbers. By taking the greatest number of times each prime factor occurs in one number, you can multiply those factors together to arrive at the least common multiple.

💡denominator

The denominator is the bottom number in a fraction. When fractions have different denominators, it can be hard to tell which fraction is larger. By finding a common denominator, you can rewrite the fractions so the denominators are the same, making comparison easier.

💡magnitude

The magnitude of a fraction refers to its relative size or value. The process of finding a common denominator allows you to rewrite fractions so you can more clearly see their relative magnitudes when comparing them.

💡alter

Alter means to change something. When finding a common denominator for fractions, you can multiply the numerator and denominator of a fraction by the same number without altering the fraction's magnitude, because anything multiplied by 1 remains the same.

💡necessarily

The video states that the product of two numbers will necessarily have those numbers as factors. This means that by the nature of multiplication, if you multiply numbers together, the result will for certain contain those original numbers in its prime factorization.

💡tedious

Tedious means boring, dull, or time-consuming. The process of writing out all the multiples of numbers to find common multiples can become tedious as the numbers get larger. That's why methods like prime factorization are preferred for larger numbers.

💡tricky

Some fraction comparisons are tricky when the denominators differ. Finding a common denominator makes comparing the magnitudes of tricky fractions with different denominators more straightforward.

💡obvious

For simple fractions like 1/3 and 1/4, it's obvious just by looking at them which is larger. But the process of finding a common denominator makes comparing the relative sizes even more obvious and clear.

Highlights

A multiple is a number that you get when you multiply a number by the positive integers.

The least common multiple of two numbers is the smallest number that is in the multiplication tables of both numbers.

The least common multiple of two numbers is often the product of the two numbers.

The product of two numbers will always be a common multiple, but it may not be the least common multiple.

To find the least common multiple of large numbers, find the prime factorization of each number.

Take the prime factors that appear in either number and multiply them together the most times they appear.

Finding common denominators using least common multiples makes comparing fractions easier.

Multiplying the numerator and denominator of a fraction by the same number does not change the fraction's value.

Once fractions have a common denominator, the one with the larger numerator is the larger fraction.

Finding common denominators for fractions using least common multiples makes comparing sizes of fractions clearer.

A multiple of a number contains that number as a factor.

Listing multiples helps identify the least common multiple between numbers.

Least common multiple provides a method to identify the smallest shared multiple.

Finding greatest common factor and least common multiple relates numbers.

Understanding least common multiples builds foundation for more complex math concepts.

Transcripts

Browse More Related Video

How To Find The LCM and HCF Quickly!

How To Find The LCM of 3 Numbers - Plenty of Examples!

GED MATH 2024 Preparation Course - from the Absolute Beginning to Advanced Level

Math Antics - Common Denominator LCD

Greatest Common Factor (GCF)

Using the Least Common Multiple to Balance