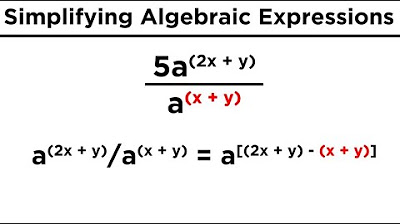Understanding Exponents and Their Operations
TLDRThe video explains the concept of exponents, where a base number is multiplied by itself a certain number of times as indicated by the exponent. It covers exponent rules like products, quotients, and powers of powers. An Indian legend demonstrates exponential growth, where rice grains on a chessboard double each square, quickly leading to immense quantities. The video explains and provides examples of positive and negative exponents and why anything to the zero power equals one. Overall it aims to build an intuitive understanding of exponents and their mathematical properties.
Takeaways
- 😀 Exponents represent repeated multiplication - raising a number to a power is multiplying it by itself that many times
- 👆 Squaring a number means multiplying it by itself twice. Cubing means multiplying it by itself 3 times.
- 😮 Exponents allow numbers to get very large, very quickly due to exponential growth
- 💡 Negative exponents invert the number - x to the -n power is 1 over x to the nth power
- 🤓 There are rules for manipulating terms with exponents: multiplication is adding the exponents, division is subtracting them
- 🧐 Anything raised to the 0 power equals 1, because there's no exponents left after dividing
- 🤯 The chessboard legend demonstrates exponential growth doubling each square
- 😊 By the 4th row, there were already over 2 billion grains of rice required
- 😲 On the final square, over a quintillion grains were needed - more rice than exists on Earth!
- 🧠 Learning the rules helps simplify expressions and understand negative exponents
Q & A
What are the four basic arithmetic operations?
-The four basic arithmetic operations are addition, subtraction, multiplication, and division.
What does raising a number to a power or exponent mean?
-Raising a number to a power or exponent represents repeated multiplication. For example, two to the third power is two multiplied by itself three times, which is eight.
What do we call a number when we raise it to the second power?
-When we raise a number to the second power, we are squaring that number. For example, five squared.
What happens when we raise something to a negative exponent?
-When raising to a negative exponent, we invert the term and make the exponent positive. For example, two to the negative two equals one fourth.
What is the rule for multiplying terms with exponents?
-The rule is: X to the A times X to the B equals X to the A plus B. This combines the exponents when multiplying terms.
What is the rule for dividing terms with exponents?
-The rule for dividing is: X to the A over X to the B equals X to the A minus B. This subtracts the exponents when dividing terms.
Why does anything raised to the zero power equal one?
-When the exponents subtract to zero, all the base terms cancel, leaving just 1. So anything to the zero power equals 1.
What was the old Indian legend described in the passage?
-It was a legend about a wise man who invented chess and asked the king to place grains of rice on a chessboard, doubling each square. This showed exponential growth.
On which chessboard square did the king have to place over a quintillion grains of rice?
-The final, 64th square required over a quintillion grains of rice, showing the immense magnitude of exponents.
What common mistake should be avoided when working with exponents?
-A common mistake is trying to combine X to the A plus X to the B. Those are separate terms that can't be combined, only multiplied/divided terms can be combined.
Outlines
🧑🏫 Introducing Exponents and Demonstrating their Immense Power through Examples
This paragraph introduces the concept of exponents, explaining that they represent repeated multiplication just as multiplication represents repeated addition. It provides examples of squaring and cubing numbers, shows alternate exponent notation, and demonstrates the immense scale exponents enable using a story about rice on a chessboard doubling each square.
📐 Rules for Manipulating Terms with Exponents and Rationale Behind Them
This paragraph explains rules like X^A * X^B = X^(A+B) and the logic behind such rules. It covers division, negative exponents, zero exponents, and exponents within exponents. It also notes that X^A + X^B cannot be combined.
Mindmap
Keywords
💡Exponent
💡Exponential growth
💡Base
💡Squared
💡Cubed
💡Negative exponent
💡Manipulating exponents
💡Zero exponent
💡Chessboard legend
💡Doubling
Highlights
Exponents represent repeated multiplication.
When we raise something to the second power, we are squaring that number.
When we raise something to the third power, we are cubing that number.
With exponents, numbers get very big very fast.
The legend shows exponential growth by repeatedly doubling the grains of rice on each square.
Negative exponents invert the term and make the exponent positive.
Rules allow manipulating terms raised to exponents.
Anything raised to the zero power equals one.
Don't make the common mistake of trying to combine terms with different exponents.
X to the A times X to the B equals X to the A plus B.
X to the A over X to the B equals X to the A minus B.
(X to the A) to the B equals X to the A times B.
Two to a high exponent shows the vast quantity of rice needed on a chess board.
The king found fulfilling the wise man's request impossible.
Luckily the wise man allowed the king to pay in installments.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: