Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (40 of 92) What is Reduced Mass?
TLDRThis script delves into the concept of reduced mass in the context of a diatomic molecule, such as carbon monoxide, explaining its relevance to the natural frequency of oscillation. It illustrates how reduced mass is calculated as a function of the masses of the two atoms and how it simplifies when one mass is significantly larger or when the masses are equal. The importance of reduced mass in determining the angular frequency of a quantum harmonic oscillator is highlighted, emphasizing the discrete quantum values as opposed to continuous values in classical harmonic oscillators.
Takeaways
- 📐 The concept of a reduced mass is introduced as it relates to a harmonic or quantum oscillator, specifically in the context of a diatomic molecule like carbon monoxide (CO).
- 🔍 The reduced mass (μ) is calculated as the product of the two masses (m1 and m2) divided by the sum of the two masses (m1 + m2), and is relevant for the frequency of oscillation in a diatomic molecule.
- 🌟 The mass of a carbon atom (C) is 12 atomic mass units (amu), which is equivalent to 12 times 1.67 × 10^-27 kilograms.
- 🌬️ The mass of an oxygen atom (O) is 16 amu, or 16 times the mass of one amu in kilograms.
- 🧪 For CO, the reduced mass is approximately 6.86 amu, which translates to about 1.145 × 10^-26 kilograms when converted.
- 🔄 The reduced mass simplifies to the larger mass if one mass is significantly greater than the other (e.g., m1 is 1000 times m2).
- ⚖️ When the two masses in a diatomic molecule are equal, the reduced mass is half the mass of either atom.
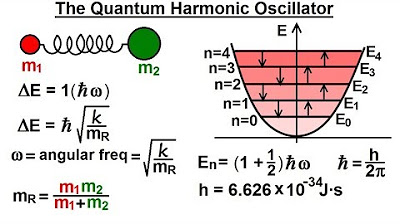
- 🌈 The reduced mass is a crucial factor in determining the angular frequency of oscillation for a simple harmonic or quantum harmonic oscillator.
- 🚫 Unlike classical harmonic oscillators, quantum harmonic oscillators can only have discrete (quantum) values, not continuous ones.
- 🔑 The angular frequency (ω) of a diatomic molecule is given by the square root of the spring constant (k) divided by the reduced mass (μ).
- 🔍 The spring constant is related to the intermolecular forces between the two atoms in a diatomic molecule and will be discussed in more detail later.
Q & A
What is the significance of the reduced mass in the context of a quantum harmonic oscillator?
-The reduced mass is crucial in determining the angular frequency of oscillation for a quantum harmonic oscillator, as it is part of the formula where the angular frequency is equal to the square root of the spring constant divided by the reduced mass.
How is the reduced mass of a diatomic molecule like carbon monoxide calculated?
-The reduced mass of a carbon monoxide molecule is calculated by taking the product of the masses of the carbon (m1) and oxygen (m2) atoms and dividing it by the sum of the two masses (m1 + m2).
What are the units for the mass of carbon and oxygen in the context of the reduced mass calculation?
-The mass of carbon is 12 atomic mass units, which is equivalent to 12 times 1.67 × 10^-27 kilograms, and the mass of oxygen is 16 atomic mass units, equivalent to 16 times the mass of one atomic mass unit in kilograms.
What is the approximate reduced mass of a carbon monoxide molecule?
-The approximate reduced mass of a carbon monoxide molecule is 6.86 atomic mass units, which转换成 kilograms is about 1.145 × 10^-26 kilograms.
How does the reduced mass relate to the relative sizes of the two masses in an oscillator?
-If one mass is much larger than the other, the reduced mass is approximately equal to the larger mass. If the masses are equal, the reduced mass is simply half the mass of either one.
What happens to the reduced mass if the two atoms in the oscillator have significantly different masses?
-If the two atoms have significantly different masses, the reduced mass will be close to the mass of the heavier atom.
What is the role of the spring constant in the context of a diatomic molecule?
-The spring constant is related to the intermolecular forces between the two atoms in a diatomic molecule and is a factor in determining the angular frequency of oscillation.
What is the difference between a quantum harmonic oscillator and a simple harmonic oscillator?
-A quantum harmonic oscillator can only have quantum values, not continuous values, which is a significant difference from a simple harmonic oscillator that can have continuous values.
How does the reduced mass affect the angular frequency of a diatomic molecule?
-The angular frequency of a diatomic molecule is inversely proportional to the reduced mass, meaning that a smaller reduced mass results in a higher angular frequency of oscillation.
If we had a diatomic molecule with equal masses, like oxygen or nitrogen, how would the reduced mass be determined?
-For a diatomic molecule with equal masses, the reduced mass would be half the mass of either atom, as the two masses are equal.
What is the importance of understanding the reduced mass in the study of molecular physics?
-Understanding the reduced mass is important as it helps in calculating key properties of molecules such as their angular frequency of oscillation, which is essential for studying their vibrational modes and energy levels.
Outlines
📚 Introduction to Reduced Mass and Quantum Harmonic Oscillators
This paragraph introduces the concept of reduced mass in the context of quantum harmonic oscillators, specifically using the example of a diatomic molecule like carbon monoxide. It explains how the reduced mass is calculated by taking the product of the two masses and dividing it by the sum of the two masses. The paragraph also discusses the relationship between the reduced mass and the natural frequency of the oscillator, highlighting that the reduced mass is a crucial factor in determining the angular frequency of oscillation. Furthermore, it explores how the reduced mass behaves relative to the sizes of the two individual masses, noting that if one mass is significantly larger than the other, the reduced mass approaches the larger mass, and if the masses are equal, the reduced mass is half the mass of either atom.
Mindmap
Keywords
💡Electron Line
💡Harmonic Oscillator
💡Quantum Oscillator
💡Reduced Mass
💡Diatomic Molecule
💡Spring Constant
💡Frequency of Oscillation
💡Intermolecular Forces
💡Carbon Monoxide
💡Atomic Mass Units
💡Angular Frequency
Highlights
The discussion focuses on the relationship between a quantum harmonic oscillator and a real-world example, specifically a diatomic molecule like carbon monoxide.
The carbon monoxide molecule is used as an example, with carbon (m1) and oxygen (m2) atoms having distinct masses.
The concept of reduced mass is introduced as a key factor in understanding the frequency of oscillation for a diatomic molecule.
The formula for calculating the reduced mass of a diatomic molecule is provided, which is the product of the two masses divided by their sum.
The mass of carbon is given as 12 atomic mass units, which转换成 kilograms is 12 times 1.67 × 10^-27 kg.
The mass of oxygen is 16 atomic mass units,转换成 kilograms as 16 times the mass of one atomic mass unit.
The reduced mass of carbon monoxide is calculated to be approximately 6.86 atomic mass units.
In kilograms, the reduced mass of carbon monoxide is about 1.145 × 10^-26 kg.
The importance of the spring constant in determining the angular frequency of a molecule is mentioned, with a promise to discuss it in more detail later.
The reduced mass can be intuitively understood as being closer to the larger mass when there is a significant mass difference between the two atoms in a diatomic molecule.
When the masses of the two atoms in a diatomic molecule are equal, the reduced mass is simply half the mass of one atom.
The concept of reduced mass is crucial for calculating the angular frequency of oscillation for a quantum harmonic oscillator.
Quantum harmonic oscillators can only have quantum values, unlike simple harmonic oscillators which can have continuous values.
The angular frequency of a quantum harmonic oscillator is determined by the reduced mass and the spring constant.
The example of carbon monoxide illustrates how the reduced mass can be calculated for real-world diatomic molecules.
The theoretical discussion provides a practical understanding of how molecular properties relate to quantum mechanics.
The transcript serves as an educational resource for understanding the principles behind quantum harmonic oscillators and their real-world applications.
The relationship between reduced mass and the angular frequency of oscillation is a fundamental concept in molecular physics.
Transcripts
Browse More Related Video
Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (39 of 92) What is the Quantum Oscillator?
Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (51 of 92) Oscillator Amplitude - Diatomic
Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (42 of 92) k=? of a Diatomic Molecule

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (46 of 92) Quantum Nature of Oscillator 2

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (38 of 92) Simple Harmonic Oscillator

Advanced Quantum Mechanics Lecture 3
5.0 / 5 (0 votes)
Thanks for rating: