Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (51 of 92) Oscillator Amplitude - Diatomic

Michel van Biezen
9 Apr 201803:32
EducationalLearning
32 Likes 10 Comments

TLDRThe video script delves into the comparison between a quantum-mechanical oscillator and a classical mechanical oscillator, using the example of a carbon monoxide molecule. It explains how quantum mechanics equations must align with classical mechanics, detailing the molecule's spring constant, amplitude at the zero energy level, reduced mass, and oscillation frequency. The script then applies classical mechanics formulas to determine the position, velocity, and acceleration of the oscillator, ultimately showing that quantum-mechanical oscillators adhere to Newton's second law and the principles of classical mechanical oscillators, providing insights into the behavior of particles at the quantum level.

Takeaways
  • 🌟 Quantum-mechanical oscillators can be compared to classical mechanical oscillators to understand their behavior.
  • πŸ“ The spring constant for the carbon monoxide molecule is 1926 Newtons per meter.
  • πŸ“ The amplitude at the zero energy level (n=0) in the quantum mechanical stage is 4.7Γ—10^-12 meters.
  • πŸ”„ The oscillation frequency is 4.1Γ—10^14 radians per second, not oscillations per second.
  • πŸ“ˆ The position of a classical oscillator over time can be described by amplitude times sine or cosine of Omega T.
  • πŸš€ The velocity of a classical oscillator is given by Omega times cosine of Omega T.
  • πŸ’₯ The maximum acceleration of a quantum mechanical Slater is 7.96Γ—10^17 meters per second squared.
  • πŸ”§ Newton's second law (F=MA) applies to quantum mechanical oscillators, relating force to mass and acceleration.
  • 🌐 The maximum force experienced by a quantum mechanical oscillator is due to intermolecular forces at the maximum amplitude of oscillation.
  • πŸ”’ The spring constant derived from the quantum mechanical model matches the classical mechanical spring constant when comparing maximum forces.
  • 🎯 The quantum mechanical oscillator follows the same rules and regulations as the classical mechanical oscillator, as shown by the consistency in force and acceleration calculations.
Q & A

  • What is the purpose of comparing a quantum-mechanical oscillator to a classical mechanical oscillator?

    -The purpose is to demonstrate that quantum mechanical equations must match classical mechanical predictions in order to be considered correct, thereby showing the connection and consistency between quantum and classical mechanics.

  • What was the spring constant determined for the carbon monoxide molecule in the discussion?

    -The spring constant for the carbon monoxide molecule was determined to be 1926 Newtons per meter.

  • What is the amplitude at the zero energy level in the quantum mechanical model?

    -At the zero energy level (n=0), the amplitude is 4.7 times 10 to the minus 12 meters.

  • What is the reduced mass calculated for the oscillation?

    -The reduced mass for the oscillation was calculated to be 1.1 times 10 to the minus 26 kilograms.

  • What is the oscillation frequency of the carbon monoxide molecule?

    -The oscillation frequency is 4.1 times 10 to the 14 radians per second.

  • How is the position of a classical mechanical oscillator expressed as a function of time?

    -The position of a classical mechanical oscillator is expressed as the amplitude times the sine or cosine of Omega T.

  • What is the relationship between the maximum amplitude and the energy state of the quantum mechanical oscillator?

    -The maximum amplitude of the quantum mechanical oscillator is related to the energy state through the equation a Max = a * Omega squared, where 'a' is the amplitude and Omega is the angular frequency.

  • How does Newton's second law relate to the force experienced by a quantum mechanical oscillator?

    -According to Newton's second law (F=MA), the force experienced by a quantum mechanical oscillator is equal to the mass times the acceleration, which can be calculated using the spring constant and the maximum amplitude.

  • What is the maximum force experienced by the carbon monoxide molecule at the maximum amplitude of oscillation?

    -The maximum force experienced at the maximum amplitude of oscillation is 9.12 times 10 to the minus 9 Newtons.

  • How does the maximum force relate to the spring constant and the amplitude?

    -The maximum force is calculated by multiplying the spring constant (K) by the maximum amplitude (A), which in this case confirms the consistency between quantum mechanics and classical mechanics.

  • What conclusion can be drawn from the analysis of the quantum mechanical oscillator in relation to Newton's laws and classical mechanics?

    -The analysis shows that even the quantum mechanical oscillator follows the same rules and regulations as described by Newton's second law and the properties of a classical mechanical oscillator, thus bridging the gap between quantum and classical descriptions of physical systems.

Outlines
00:00
πŸ“ Quantum-Mechanical Oscillator Comparison

This paragraph introduces the concept of a quantum-mechanical oscillator by comparing it to a classical mechanical oscillator. It discusses the carbon monoxide molecule's spring constant, amplitude at the zero energy level, reduced mass, and oscillation frequency. The paragraph explains how the position, velocity, and acceleration of an oscillator can be described using classical mechanics equations. It then calculates the maximum acceleration and force experienced by the quantum-mechanical oscillator at its maximum amplitude, demonstrating that quantum-mechanical oscillators follow Newton's second law and the rules of classical mechanical oscillators.

Mindmap
Keywords
πŸ’‘Quantum-mechanical Slayer
The term 'Quantum-mechanical Slayer' seems to be a misinterpretation or typo in the transcript, likely referring to a 'quantum-mechanical oscillator'. A quantum-mechanical oscillator is a system that can be described by the principles of quantum mechanics and exhibits oscillatory behavior. In the context of the video, it is compared to a classical mechanical oscillator to understand the similarities and differences in their behavior. The quantum-mechanical oscillator is used to illustrate how quantum mechanics can explain phenomena at the atomic and subatomic levels, which classical mechanics cannot fully account for.
πŸ’‘Classical mechanical oscillator
A classical mechanical oscillator is a system that oscillates under the influence of restoring forces according to the laws of classical mechanics. It is characterized by its ability to store potential and kinetic energy and to undergo periodic motion. The classical oscillator is used as a comparison to the quantum-mechanical oscillator to highlight the differences in how each system responds to energy and force.
πŸ’‘Spring constant
The spring constant, often denoted by k, is a measure of the stiffness of a spring. It defines the relationship between the force applied to the spring and the amount of stretch or compression it undergoes. In the context of the video, the spring constant for the carbon monoxide molecule is given as 1926 Newtons per meter, which is used to calculate the force and motion of the molecule as it oscillates.
πŸ’‘Amplitude
Amplitude in the context of oscillations refers to the maximum displacement of the oscillating object from its equilibrium position. It is a measure of the extent of the oscillation. In the video, the amplitude of the quantum-mechanical oscillator at the zero energy level (n=0) is calculated to be 4.7 times 10 to the minus 12 meters, indicating the scale of the molecule's movement.
πŸ’‘Reduced mass
The reduced mass is a concept used in the two-body problem in physics to simplify the analysis of the motion of two objects bound by a force, such as a spring. It is the product of the two masses involved divided by the sum of their masses. In the context of the video, the reduced mass for the carbon monoxide molecule is calculated to be 1.6 times 10 to the minus 26 kilograms, which is important for determining the oscillation frequency and the dynamics of the system.
πŸ’‘Oscillation frequency
The oscillation frequency is the rate at which an oscillator completes its cycle of motion. It is measured in units of cycles per second, or Hertz (Hz). In the context of the video, the oscillation frequency for the carbon monoxide molecule is given in radians per second, which is a measure of how quickly the molecule oscillates around its equilibrium position.
πŸ’‘Angular frequency (Omega)
Angular frequency, symbolized by Omega (Ο‰), is a measure of how quickly an object rotates or oscillates around a central point. It is related to the linear frequency (f) by the equation Ο‰ = 2Ο€f. In physics, angular frequency is used to describe oscillatory motion, such as that of a quantum-mechanical or classical mechanical oscillator. In the video, angular frequency is used to express the position and velocity of the oscillator as a function of time.
πŸ’‘Maxwell's equations
While not explicitly mentioned in the script, Maxwell's equations are a set of fundamental equations in physics that describe the behavior of electric and magnetic fields. They are essential for understanding electromagnetism and would be relevant in the context of quantum mechanics as they govern the classical behavior of electromagnetic waves, which can be quantized to form photons.
πŸ’‘Newton's second law (F=ma)
Newton's second law of motion states that the force (F) acting on an object is equal to the mass (m) of the object multiplied by its acceleration (a). This law is fundamental in classical mechanics and describes the relationship between force, mass, and motion. In the video, Newton's second law is used to calculate the maximum force experienced by the oscillating molecule, demonstrating that quantum-mechanical oscillators also follow classical physical laws.
πŸ’‘Intermolecular forces
Intermolecular forces are the forces that occur between molecules, influencing their physical properties such as boiling points, melting points, and solubility. These forces include van der Waals forces, hydrogen bonding, and others. In the context of the video, intermolecular forces are discussed in relation to the maximum force experienced by the carbon monoxide molecule during its oscillation, which is a result of the spring-like interaction between its atoms.
πŸ’‘Energy levels
In quantum mechanics, energy levels refer to the discrete amounts of energy that a system can have. These are the allowed energy states of the system, and the system can only transition between these states. In the context of the video, the energy levels are discussed in relation to the quantum-mechanical oscillator, where the zero energy level (n=0) corresponds to a specific amplitude of oscillation.
πŸ’‘Total distance between atoms
The total distance between atoms refers to the equilibrium separation between two atoms in a molecule or an atomic system. This distance is determined by the balance of attractive and repulsive forces between the atoms. In the context of the video, the total distance between atoms is used as a reference to understand the percentage of the oscillation amplitude, indicating the extent of the molecule's oscillation relative to its bond length.
Highlights

Comparing a quantum-mechanical oscillator to a classical mechanical oscillator to understand the similarities and differences.

The spring constant of the carbon monoxide molecule is 1926 Newtons per meter.

The amplitude at the zero energy level in the quantum mechanical stage is 4.7 x 10^-12 meters.

The reduced mass for the oscillation frequency is 1.1 x 10^-26 kilograms.

The oscillation frequency is 4.1 x 10^14 radians per second.

The position of a classical oscillator as a function of time can be expressed as the amplitude times the sine or cosine of Omega T.

The velocity of a classical oscillator is given by Omega times the cosine of Omega T.

The maximum acceleration of a quantum mechanical oscillator is calculated to be 7.96 x 10^17 meters per second squared.

Newton's second law (F=MA) is used to calculate the force on the quantum mechanical oscillator.

The maximum force experienced by the spring is due to intermolecular forces at the maximum amplitude.

The force calculated using the spring constant matches the force calculated using Newton's second law.

Quantum mechanical oscillators follow the same rules and regulations as classical mechanical oscillators.

The maximum force (F_max) is experienced when the spring is pulled back to its maximum amplitude.

The analysis provides a good understanding of quantum mechanical oscillators and their energy levels.

The percentage of the total distance between atoms is considered when evaluating the oscillation amplitudes.

The transcript explains the mathematical and physical principles behind quantum and classical oscillators in detail.

Transcripts

Browse More Related Video

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (48 of 92) How Oscillator Increases energy

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (38 of 92) Simple Harmonic Oscillator

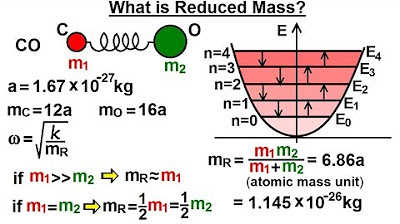
Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (40 of 92) What is Reduced Mass?

Advanced Quantum Mechanics Lecture 3

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (44 of 92) What is the Selective Rule?

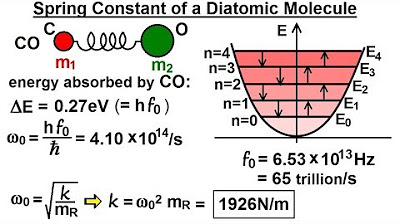
Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (42 of 92) k=? of a Diatomic Molecule

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
QuantumMechanicsClassicalOscillatorsMolecularPhysicsNewtonsLawsIntermolecularForcesOscillationAmplitudeEnergyLevelsPhysicsEducationSchrodingerEquationSpringConstant