Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (38 of 92) Simple Harmonic Oscillator

Michel van Biezen
28 Mar 201805:31
EducationalLearning
32 Likes 10 Comments

TLDRThe video script delves into the classical and quantum mechanical models of a simple harmonic oscillator. It explains the potential energy graph, the relationship between mass, spring constant, and oscillation, and how the maximum potential energy is represented. The script then transitions to quantum mechanics, highlighting the difference in energy equations and introducing the concept of quantized energy levels, which restricts the possible energy values for a particle in contrast to the classical model where all energy values are possible.

Takeaways
  • ๐Ÿ“ˆ The potential energy graph of a classical simple harmonic oscillator is used to understand its behavior.
  • ๐Ÿ”„ A mass (M) on a spring (K) oscillates, with potential energy represented by the equation 1/2 KX^2.
  • ๐Ÿ At maximum extension, the oscillator has maximum potential energy (1/2 K a^2), and at the equilibrium position, potential energy is zero, where kinetic energy is maximum.
  • ๐ŸŒ The total energy of the system is the sum of kinetic and potential energy.
  • ๐Ÿ“ The quantum mechanical equations for the harmonic oscillator differ slightly from the classical model but are equivalent.
  • ๐ŸŒ€ The angular frequency (Omega) is related to the spring constant (K) and mass (M) by the equation Omega = sqrt(K/M).
  • ๐Ÿ”„ The maximum potential energy can also be expressed as 1/2 M Omega^2 a^2, showing equivalence with the classical model.
  • ๐Ÿƒ The probability of finding a particle at a certain position (X) is inversely proportional to its velocity at that point.
  • ๐Ÿ“Š The probability density is proportional to the width of the position interval (DX) and inversely proportional to the velocity of the particle.
  • ๐Ÿšซ In the classical model, all energy values are possible, unlike in quantum mechanics where certain energy values are not permissible.
  • ๐Ÿ’ก The understanding of energy quantization in the quantum harmonic oscillator will be explored in the next video.
Q & A

  • What is the classical model of a simple harmonic oscillator?

    -The classical model of a simple harmonic oscillator involves a mass (M) oscillating back and forth on a spring with a spring constant (K). The potential energy of the system can be represented by the graph of 1/2 KX^2, where X is the displacement from the equilibrium position.

  • How is the maximum potential energy of the oscillator represented in the classical model?

    -In the classical model, the maximum potential energy is represented by 1/2 K*a^2, which occurs at the maximum extension in one direction (X = -a) or the maximum compression in the other direction (X = a).

  • What is the relationship between the potential energy and the angular frequency in the quantum mechanical model of a simple harmonic oscillator?

    -In the quantum mechanical model, the potential energy is related to the angular frequency (Omega) by the equation 1/2 K*X^2 = 1/2 M*Omega^2 * X^2. This shows that the potential energy can also be expressed as 1/2 M * Omega^2 * a^2, where a is the maximum displacement.

  • How is the angular frequency (Omega) of an oscillator defined?

    -The angular frequency (Omega) of an oscillator is defined as the square root of the spring constant (K) divided by the mass (M), or Omega = sqrt(K/M). It is also equal to 2*pi times the frequency of oscillation.

  • What does the total energy of a simple harmonic oscillator consist of?

    -The total energy of a simple harmonic oscillator consists of the sum of its kinetic energy and potential energy. At the maximum displacement, the potential energy is at its maximum, and the kinetic energy is zero, and vice versa at the equilibrium position.

  • How is the kinetic energy of a particle in a quantum harmonic oscillator related to its total energy and position?

    -The kinetic energy of a particle in a quantum harmonic oscillator can be expressed in terms of the total energy (E_max) minus the potential energy (V) at a given position (X). This relationship is derived from the equation 1/2 M * V^2 = E_max - V.

  • What is the probability of finding a particle at a certain position in a quantum harmonic oscillator?

    -The probability of finding a particle at a certain position in a quantum harmonic oscillator is proportional to the width of the region (DX) divided by the velocity of the particle at that position. The slower the particle moves, the higher the probability of finding it there.

  • How does the classical model differ from the quantum mechanical model in terms of possible energy values?

    -In the classical model, all values of energy are possible, whereas in the quantum mechanical model, there are certain discrete energy values that cannot exist for a particle, such as a quantum harmonic oscillator.

  • What is the significance of the angular frequency in determining the energy levels of a quantum harmonic oscillator?

    -The angular frequency is crucial in determining the energy levels of a quantum harmonic oscillator because it directly influences the potential and kinetic energy equations. The energy levels in a quantum harmonic oscillator are quantized and depend on the angular frequency, which is derived from the physical properties of the system (mass and spring constant).

  • How does the potential energy graph of a classical harmonic oscillator relate to the oscillator's behavior?

    -The potential energy graph of a classical harmonic oscillator, which is parabolic, shows how the potential energy changes with the position of the mass on the spring. The shape of the graph indicates that the lowest potential energy occurs at the equilibrium position and increases symmetrically on either side, representing the restoring force that drives the oscillator back to equilibrium.

  • What is the role of the mass (M) in the energy equations of a simple harmonic oscillator?

    -The mass (M) of the oscillator plays a significant role in the energy equations as it affects both the potential energy (through the spring constant K and mass M relationship) and the kinetic energy (directly proportional to M). The mass influences the oscillator's response to the spring's force and its velocity at different positions.

Outlines
00:00
๐Ÿ“ Classical Model of the Simple Harmonic Oscillator

This paragraph introduces the classical model of the simple harmonic oscillator, discussing the potential energy graph and the mass-spring system. It explains how the potential energy varies with the position of the mass (M) on the spring with spring constant (K). The maximum potential energy is described as 1/2 K*a^2, occurring at the maximum extension in either direction. The potential energy is zero at the point of maximum kinetic energy, where the mass has the highest velocity. The equivalence between the classical and quantum mechanical equations is highlighted, showing that 1/2 K*a^2 is equal to 1/2 M*Omega^2*a^2, with Omega being the angular frequency derived from K/M. The total energy of the system is the sum of kinetic and potential energy, and the kinetic energy can be expressed in terms of the total energy, mass, angular frequency, and position. The paragraph concludes with a discussion on the probability of finding a particle at a certain position, which is inversely proportional to the velocity at that point.

05:01
๐Ÿšซ Quantum Limitations on Energy Levels

This paragraph transitions from the classical to the quantum mechanical perspective on the simple harmonic oscillator. It emphasizes that in the quantum model, not all energy values are possible, unlike in the classical model where energy can take any value. The quantum model restricts the energy to certain discrete values, a concept that will be explored further in the next video. This introduces the quantum nature of energy levels and sets the stage for understanding the quantization of energy in quantum mechanics.

Mindmap
Keywords
๐Ÿ’กSimple Harmonic Oscillator
A simple harmonic oscillator is a system that oscillates with a periodic motion, where the restoring force is directly proportional to the displacement and inversely proportional to the square of the natural frequency. In the context of the video, it refers to both the classical and quantum mechanical models of an oscillator, such as a mass attached to a spring.
๐Ÿ’กPotential Energy
Potential energy is the stored energy an object has due to its position in a force field, like a gravitational or an elastic field. In the video, the potential energy of the oscillator is represented by the graph and is given by the equation 1/2 KX^2, where X is the displacement from the equilibrium position.
๐Ÿ’กSpring Constant (K)
The spring constant, denoted by 'K', is a measure of the stiffness of a spring. It is defined as the force required to cause a unit deformation of the spring. In the video, the spring constant is used to calculate the potential energy of the system and is a key parameter in the equations of motion for the harmonic oscillator.
๐Ÿ’กMass (M)
Mass is a measure of the amount of matter in an object, and it determines the object's inertia and response to forces. In the context of the video, the mass (M) of the oscillator is a crucial factor in the equations that describe the system's motion and energy.
๐Ÿ’กQuantum Mechanics
Quantum mechanics is a fundamental theory in physics that describes the behavior of matter and energy at very small scales, such as atomic and subatomic particles. The video transitions from discussing the classical model of the harmonic oscillator to hinting at the quantum mechanical perspective, where energy levels are quantized and not all energy values are possible.
๐Ÿ’กAngular Frequency (Omega)
Angular frequency, symbolized by Omega (ฯ‰), is a measure of how quickly an object rotates or oscillates, and it is related to the frequency (f) by the equation ฯ‰ = 2ฯ€f. In the context of the video, angular frequency is used to describe the oscillation of the simple harmonic oscillator and is derived from the spring constant (K) and mass (M).
๐Ÿ’กTotal Energy
Total energy in the context of the simple harmonic oscillator refers to the sum of kinetic and potential energies. The video emphasizes that the total energy is conserved and remains constant throughout the oscillation, which is a fundamental principle in the classical model.
๐Ÿ’กKinetic Energy
Kinetic energy is the energy an object possesses due to its motion. In the video, kinetic energy is discussed as part of the energy conservation principle in the simple harmonic oscillator, where it is related to the mass of the object, its velocity, and the angular frequency.
๐Ÿ’กProbability
In quantum mechanics, probability is used to describe the likelihood of finding a particle in a particular state or position. The video introduces the concept of probability in relation to the position of the oscillator and how it varies with the oscillator's velocity.
๐Ÿ’กEnergy Quantization
Energy quantization is a principle in quantum mechanics where energy can only take on discrete values rather than a continuous range. The video hints at this concept by stating that not all energy values are possible for a small particle, unlike in the classical model.
๐Ÿ’กEquivalence of Equations
The equivalence of equations in the context of the video refers to the mathematical relationship between the classical and quantum mechanical descriptions of the simple harmonic oscillator. The video shows that despite the different forms, the underlying physics is the same.
Highlights

Introduction to the simple harmonic oscillator at the quantum mechanic level.

Comparison of classical and quantum mechanical models of the oscillator.

Explanation of potential energy graph for the oscillator.

Description of a mass with mass M oscillating on a spring with spring constant K.

Maximum potential energy in the system at maximum extension.

Equivalence of energy expressions in classical and quantum models.

Derivation of the angular frequency Omega from the spring constant and mass.

Rewriting of the potential energy equation in terms of Omega.

Explanation of the total energy as the sum of kinetic and potential energy.

Discussion on the maximum or total energy of the oscillator.

Expression for the velocity of the oscillator in terms of its mass, total energy, angular frequency, and position.

Probability of finding the particle at a certain position is inversely proportional to its velocity.

Higher probability of finding the particle at the endpoints where it moves slower.

Contrast between classical and quantum models regarding possible energy values.

In the quantum model, certain energy values are not possible for a particle.

้ข„ๅ‘Šไธ‹ไธ€่ง†้ข‘ๅฐ†่ฎจ่ฎบ้‡ๅญๅŠ›ๅญฆ่ฎพ็ฝฎไธ‹็š„็ฎ€ๅ•่ฐๆŒฏๅญใ€‚

Transcripts

Browse More Related Video

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (39 of 92) What is the Quantum Oscillator?

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (51 of 92) Oscillator Amplitude - Diatomic

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (48 of 92) How Oscillator Increases energy

AP Physics Workbook 6.I Changing Mass and Period of a Mass Spring SYstem

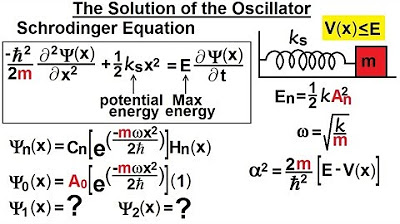
Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (55 of 92) Solution of the Oscillator

Advanced Quantum Mechanics Lecture 3

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
QuantumMechanicsSimpleHarmonicOscillatorEnergyQuantizationProbabilityDistributionClassicalPhysicsSpringConstantAngularFrequencyPotentialEnergyKineticEnergyPhysicsEducation