Where do Sin, Cos and Tan Actually Come From - Origins of Trigonometry - Part 1
TLDRThis video script delves into the origins and applications of sine, cosine, and tangent in trigonometry. It begins with a discussion on pi and its relationship with circles, then transitions to exploring right-angled triangles with specific angles. The script demonstrates how ratios of sides in these triangles can be used to develop formulas for calculating missing sides or angles, leading to the introduction of the sine, cosine, and tangent functions. It highlights the precision and utility of these functions in mathematics and science, and teases a deeper exploration in a follow-up video.
Takeaways
- 📚 The origin of sine, cosine, and tangent is explored through their representation on calculators and their mathematical significance.
- 📈 Pi (π) is derived from the ratio of a circle's circumference to its diameter, a constant value applicable to all circles.
- 📐 The concept of ratios in right-angled triangles leads to the definition of sine, cosine, and tangent.
- 🔢 For a 60-degree angle in any right-angled triangle, the ratio of the opposite side to the hypotenuse is approximately 0.866.
- 🔍 By experimenting with triangles of different sizes, the ratios for specific angles remain constant, leading to the creation of trigonometric tables.
- 📊 Trigonometric values can be plotted on a graph, forming a sine wave, which is fundamental in mathematics and science.
- 🌐 The sine, cosine, and tangent functions are defined for every angle, not just those found in right-angled triangles.
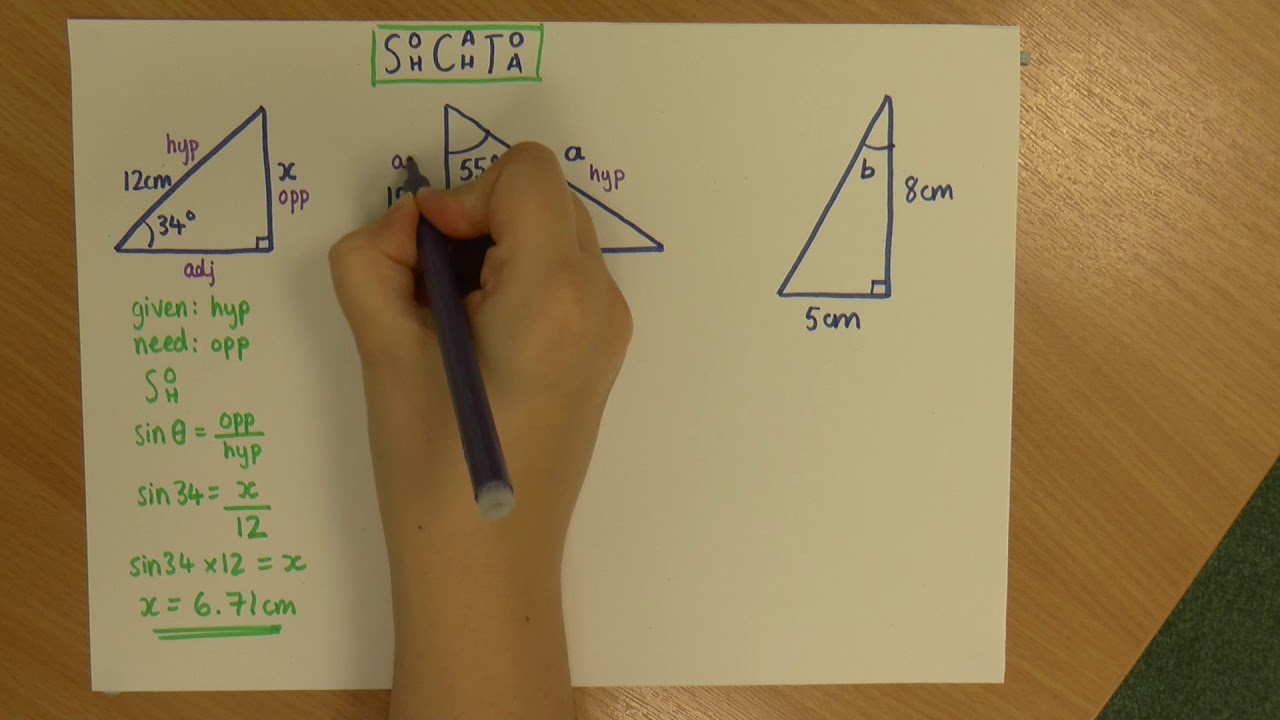
- 👩🏫 Trigonometry is taught using mnemonics like SOHCAHTOA to help students remember the relationships between angles and sides in right-angled triangles.
- 🔄 The unit circle is introduced as a more formal way to define trigonometric identities beyond the scope of right-angled triangles.
- 🎥 The video script serves as an introduction to the concepts of sine, cosine, and tangent, with a promise of a deeper exploration in a follow-up video.
- 🎓 The importance of understanding the origins and applications of these trigonometric functions is emphasized for a comprehensive grasp of mathematics.
Q & A
What are the primary functions of sine, cosine, and tangent in trigonometry?
-Sine, cosine, and tangent are fundamental trigonometric functions used to relate angles to the ratios of sides in right-angled triangles. Sine (sin) represents the ratio of the length of the side opposite the angle to the length of the hypotenuse, cosine (cos) is the ratio of the adjacent side to the hypotenuse, and tangent (tan) is the ratio of the opposite side to the adjacent side.
How is the mathematical constant pi (π) derived?
-The constant pi (π) is derived by dividing the circumference of a circle by its diameter. This value is found to be approximately 3.141, and it remains constant for every circle, regardless of size.
What is the significance of the 60-degree angle in the context of the script?
-The 60-degree angle is significant because it is used to demonstrate the concept of sine in trigonometry. For any right-angled triangle with a 60-degree angle, the ratio of the opposite side to the hypotenuse is a consistent value, approximately 0.866, which is the sine of 60 degrees.
How does the script illustrate the concept of a theorem in mathematics?
-The script illustrates the concept of a theorem by showing how a pattern observed in triangles with a 60-degree angle can be generalized into a theorem. This theorem states that for any right-angled triangle with a 60-degree angle, the ratio of the opposite side to the hypotenuse is 0.866, which is then recorded and used to find missing sides in similar triangles.
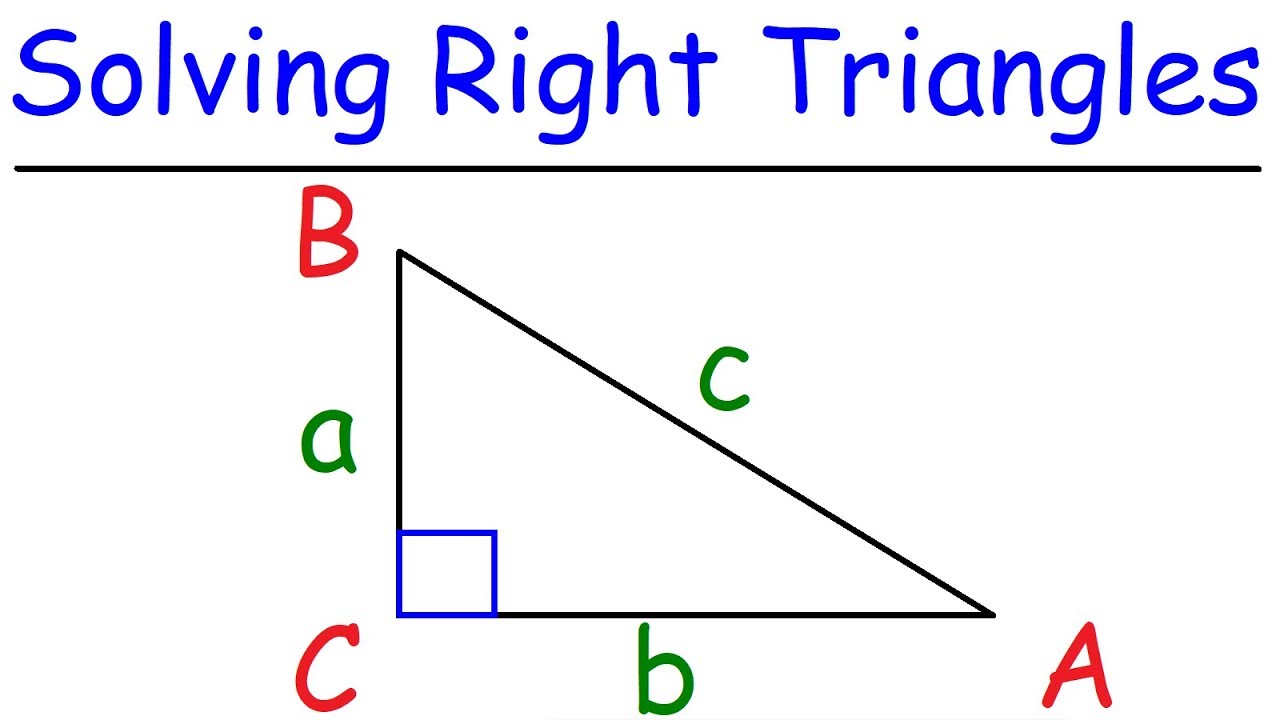
What is the relationship between the hypotenuse and the other two sides in a right-angled triangle?
-In a right-angled triangle, the hypotenuse is the longest side and is opposite the right angle (90 degrees). The other two sides are referred to as the adjacent side (next to the angle of interest but not opposite it) and the opposite side (directly opposite the angle of interest). The trigonometric functions sine, cosine, and tangent relate these sides to the angles in the triangle.
How does the script introduce the concept of the sine wave?
-The script introduces the sine wave by showing that when the ratio of the opposite side to the hypotenuse is calculated for all angles from 1 to 89 degrees in a right-angled triangle, the resulting values form a curve known as the sine wave. This wave is a fundamental concept in mathematics and science, representing the periodic nature of the sine function.
What are the limitations of using right-angled triangles to understand all trigonometric functions?
-Right-angled triangles can only be used to understand angles up to 90 degrees. Trigonometric functions like sine and cosine are periodic and can represent angles beyond 90 degrees, such as 270 degrees or -315 degrees. To understand these angles, a more formal definition using the unit circle is necessary, as mentioned in the script.
How does the script compare the manual calculation of trigonometric values to the use of a calculator?
-The script compares manual calculations by measuring the sides of right-angled triangles and dividing them to find ratios, which are then rounded to three decimal places. In contrast, using a calculator to find the sine or cosine of an angle provides a much more accurate and precise value, as these functions are pre-programmed and calculated based on a comprehensive table of values.
What is the significance of the acronym SOHCAHTOA in the script?
-SOHCAHTOA is an acronym used to help students remember the trigonometric functions: Sine (opposite/hypotenuse), Cosine (adjacent/hypotenuse), and Tangent (opposite/adjacent). The script mentions this acronym in the context of using these formulas to find missing angles or sides in right-angled triangles.
What is the purpose of the table and graph used in the script?
-The table and graph in the script serve to record and visualize the patterns found in the ratios of sides in right-angled triangles. The table helps to quickly reference these ratios for different angles, while the graph plots these ratios against the angles, revealing the sine wave pattern, which is crucial for understanding the behavior of the sine function across all possible angles.
Outlines
📚 Introduction to Trigonometric Functions
This paragraph introduces the trigonometric functions sine (sin), cosine (cos), and tangent (tan), highlighting their prevalence in mathematics and their presence on scientific calculators. It explores the historical context of these functions by discussing the concept of pi (π) and its derivation from the circumference of a circle. The paragraph then delves into the application of similar principles to right-angled triangles, specifically focusing on triangles with a 60-degree angle. By measuring and dividing the opposite side by the hypotenuse, a consistent value of 0.866 is found, leading to the formulation of a theorem that can be used to find missing sides in such triangles. The paragraph also touches on the practical application of this theorem and introduces the concept of graphical representation to identify patterns.
📈 Trigonometric Functions and Their Applications
This paragraph continues the exploration of trigonometric functions by examining their application in right-angled triangles with different angles. It starts by considering a triangle with a 30-degree angle and finds that the ratio of the opposite side to the hypotenuse is consistently 0.5. The paragraph then compares the author's method of creating a table and graph to established trigonometric tables and the sine wave, which are more comprehensive and accurate. The discussion moves on to the functions cosine (cos) and tangent (tan), explaining their derivation from the adjacent and adjacent-to-opposite sides of a right-angled triangle, respectively. The paragraph concludes by mentioning the use of sohcahtoa as a mnemonic device for trigonometric formulas and sets the stage for a more formal introduction to these identities using the unit circle in a subsequent video.
Mindmap
Keywords
💡Trigonometry
💡Sine (sin)
💡Circle
💡Pi (π)
💡Right-angled triangle
💡Hypotenuse
💡Opposite side
💡Adjacent side
💡Cosine (cos)
💡Tangent (tan)
💡Unit circle
💡SOHCAHTOA
Highlights
Sign, cos, and tan are essential functions found on every scientific calculator.
The origin of these functions is explored through the concept of pi and the relationship between a circle's circumference and diameter.
Pi is a universal constant, equal to the circle's circumference divided by its diameter, approximately 3.141.
The method of using the ratio of the sides of a right-angle triangle to understand trigonometric functions is introduced.
A 60-degree angle in a right-angle triangle consistently yields a ratio of 0.866 when the opposite side is divided by the hypotenuse.
This ratio is found to be applicable to all right-angle triangles with a 60-degree angle, regardless of size.
The concept of a theorem is used to establish a method for finding missing sides in right-angle triangles with a known angle.
A table and graph are used to record and visualize the relationships between angles and the ratios of the triangle's sides.
The sine, cosine, and tangent functions are derived from the ratios of the sides of right-angle triangles.
The sine of 60 degrees is precisely 0.866025, a value that can be found using a calculator.
The cosine function is related to the ratio of the adjacent side to the hypotenuse in a right-angle triangle.
The tangent function is associated with the ratio of the opposite side to the adjacent side.
The video discusses the limitations of using right-angle triangles to understand angles outside the range of 0 to 90 degrees.
The unit circle will be introduced in part two as a more formal way to define trigonometric identities.
The video aims to provide a basic understanding of where sine, cosine, and tangent functions come from and their practical applications.
The use of SOHCAHTOA is mentioned as a mnemonic device to help remember the trigonometric functions.
The sine wave is introduced as a pattern formed by plotting the sine function for all angles, with significant applications in math and science.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: