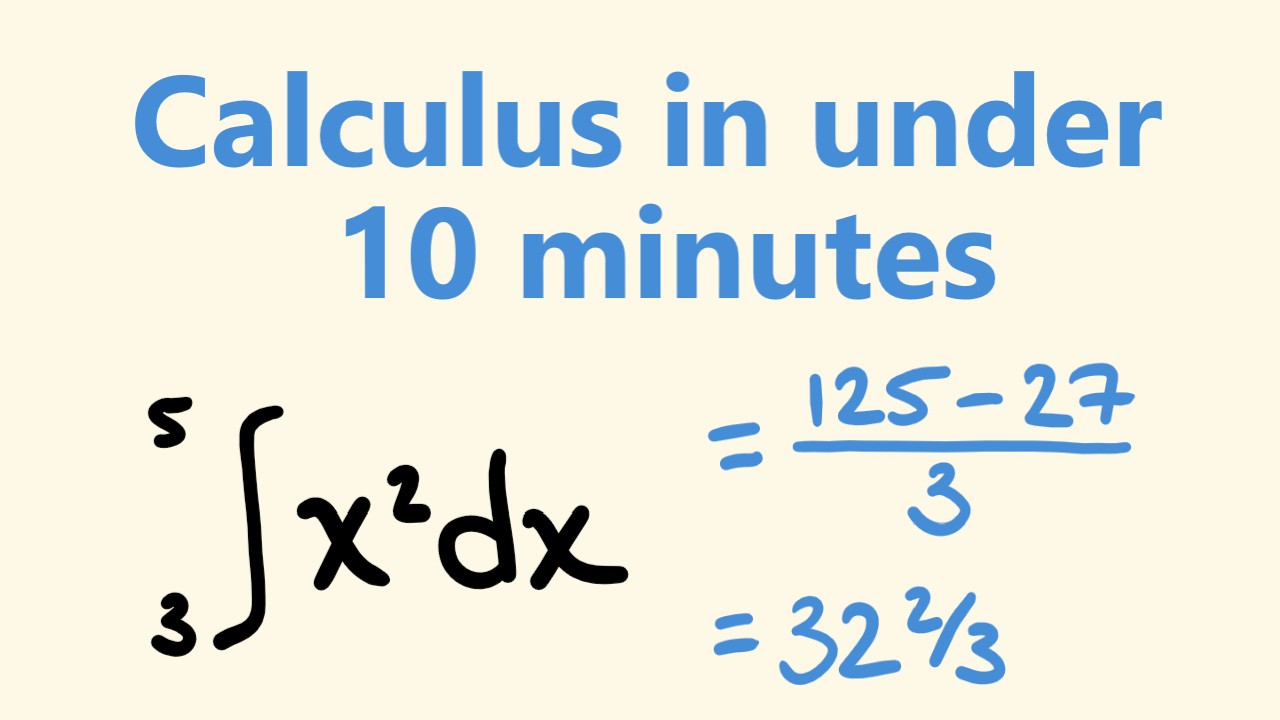How to use Calculus to solve a basic math problem
TLDRThe video script introduces the concept of calculating the area of a triangle using both basic math and calculus. The presenter, John, explains the straightforward formula for finding the area of a triangle and then demonstrates how calculus can be applied to find the area of more complex shapes where a formula may not be readily available. He emphasizes the practicality of using formulas for simple shapes but highlights the power of calculus for more intricate calculations.
Takeaways
- 📐 The base and height of the triangle are given as 4 and 3, respectively.
- 🧮 The area of the triangle is calculated using the formula: 1/2 * base * height, resulting in an area of 6 square units.
- 🌟 Introduction to calculus as a method for finding areas, even for complex shapes without a direct formula.
- 📚 The equation y = (3/4)x is used to represent the line forming the triangle, with the point (4,3) being the corner.
- 🔄 The concept of integration in calculus is introduced to find the area under a curve, using infinitely small rectangles.
- 📈 The integral of 3/4x is found to be (3/8)x^2, which is used to calculate the area of the triangle from x=0 to x=4.
- 🎯 Practical application of calculus is demonstrated, showing that it can be used for finding areas of shapes beyond basic geometric figures.
- 👨🏫 The speaker, John, is the founder of Tablet Class Math and a middle-high school math teacher, offering online math courses.
- 🔗 John invites viewers to check out his math help program and course catalog through a link in the video description.
- 📝 Emphasizes the importance of note-taking in学好 math, as it is a key factor in academic success.
- 🚀 John is preparing to launch a pre-calculus course and has various test preparation courses available.
Q & A
What is the base and height of the triangle mentioned in the script?
-The base of the triangle is 4 units and the height is 3 units.
What is the formula for the area of a triangle?
-The formula for the area of a triangle is one half the base times the height (1/2 * base * height).
What is the area of the triangle using the basic math formula?
-The area of the triangle using the basic math formula is 6 square units (1/2 * 4 * 3 = 6).
What is the equation of the line mentioned in the script?
-The equation of the line is y equals three fourths x, or y = 3/4x.
How does calculus help in finding the area of shapes?
-Calculus helps in finding the area of shapes by integrating under a curve to sum up the infinitesimally small rectangles that make up the shape's area, especially when a direct formula is not available.
What is the integral of 3/4x with respect to x?
-The integral of 3/4x with respect to x is (3/4)x^2/2, which simplifies to (3/8)x^2.
How does the script demonstrate the application of calculus in finding the area of the triangle?
-The script demonstrates the application of calculus by setting up an integral for the function y = 3/4x, evaluating it from 0 to 4, and showing that the result matches the area found using the basic formula, thus validating the use of calculus for finding areas of complex shapes.
What is the significance of the video in teaching mathematics?
-The video aims to provide an introduction to the power and usefulness of calculus, particularly in finding the areas of shapes for which direct formulas may not exist, and to encourage viewers to appreciate the broader applications of mathematical concepts.
Who is the speaker in the video and what is his profession?
-The speaker in the video is John, the founder of Tablet Class Math and a middle-high school math teacher.
What types of math courses does John offer?
-John offers over 100 different math courses ranging from pre-algebra to advanced mathematics, as well as test preparation courses for various exams such as GED, SAT, ACT, GRE, GMAT, and others.
What advice does John give to students who are serious about improving their math skills?
-John advises students to take note-taking seriously, as those who consistently take good notes tend to perform better in math. He also emphasizes that there are no shortcuts and that dedication and effort are required to improve in mathematics.
Outlines
📐 Introduction to Finding the Area of a Triangle
The video begins with an introduction to calculating the area of a triangle with given dimensions, specifically a right triangle with a base of 4 and a height of 3. The speaker, John, emphasizes the importance of understanding basic mathematical formulas and also introduces the concept of using calculus as an alternative method for finding areas, even for more complex shapes.
🧮 Basic Math vs Calculus for Area Calculation
John demonstrates the straightforward method of calculating the area of the triangle using the basic formula (1/2 * base * height), resulting in an area of 6 square units. He then transitions into explaining the concept of using calculus to find the area, emphasizing its utility for more complex shapes without a direct formula. The video aims to showcase the power and application of calculus beyond just academic exercises.
📚 Understanding Calculus and Integration
The speaker delves into the mechanics of using calculus to find the area of the triangle. He explains the concept of integration, which involves finding the area under a curve by summing infinitesimally small rectangles. John illustrates how to set up the integral for the function y = (3/4)x and how to evaluate it to find the area of the triangle, highlighting the general process without going into advanced calculus details.
🎓 Practicality and Applications of Calculus
John concludes by reflecting on the practicality of using calculus for simple tasks like finding the area of a basic triangle, acknowledging that it's not practical in this case but emphasizing its importance for more complex shapes. He encourages viewers to explore calculus for its problem-solving capabilities and promotes his math help program for those interested in deepening their mathematical understanding.
Mindmap
Keywords
💡Area
💡Triangle
💡Base
💡Height
💡Formula
💡Calculus
💡Integration
💡Power Rule
💡Tablet Class Math
💡Note-taking
Highlights
The speaker introduces the task of finding the area of a triangle with a base of 4 and a height of 3.
The formula for the area of a triangle is mentioned as 1/2 times base times height.
The area of the triangle is calculated using basic math to be 6 square units.
The speaker then introduces the concept of using calculus to find the area of the same triangle.
The equation y equals three fourths x is given as the line forming the triangle.
The speaker emphasizes the usefulness of calculus in finding areas of complex shapes without a formula.
An introduction to the founder of Tablet Class Math and his online math health program is provided.
The speaker explains the importance of note-taking in learning and improving in mathematics.
The concept of integration in calculus is introduced to find the area under a curve.
The integral of 3/4 x is calculated to demonstrate the basic mechanics of calculus.
The area of the triangle is confirmed to be 6 square units using calculus, mirroring the basic math approach.
The speaker discusses the practicality of using calculus for simple geometric shapes versus complex figures.
The video aims to showcase the power and application of calculus in problem-solving.
The speaker invites viewers to explore his YouTube channel and math health program for further learning.
The importance of understanding basic algebra for grasping the concepts of calculus is mentioned.
The video concludes with a call to action for viewers to engage with the speaker's content and pursue learning in mathematics.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: