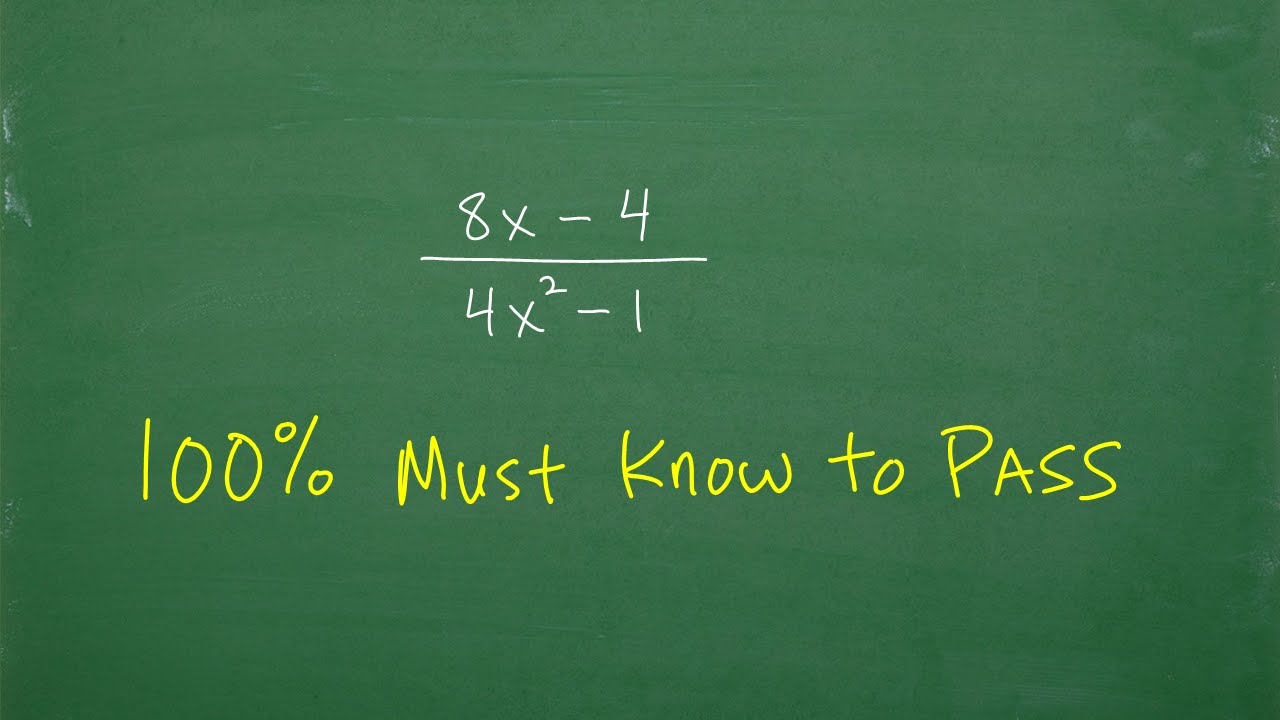Terrible at Factoring trinomials? Do this…
TLDRIn this instructional video, John, the founder of TabletClass Math, addresses the common struggle students face with factoring trinomials in algebra. He introduces two cases of trinomial factoring, providing a step-by-step method for each, ensuring a clear understanding of the process. John emphasizes the importance of mastering factoring as a fundamental algebra skill and offers his online math help program for further assistance. The video is designed to guide students through the complexities of factoring, aiming to demystify the subject and improve their algebraic abilities.
Takeaways
- 📚 Factoring is a critical skill in algebra that can be confusing for beginners but is essential to master.
- 👨🏫 The speaker, John, is a math teacher and founder of TabletClass Math, offering online math help programs for various courses and exams.
- 🔍 There are different approaches to factoring trinomials, and the video introduces a systematic method to tackle them, especially for those who struggle.
- 📈 The importance of note-taking in learning mathematics is emphasized, as it is a non-negotiable aspect of mastering the subject.
- 📝 Students are advised to put away distractions like cell phones and be fully engaged in the learning process to improve note-taking skills.
- 📉 The video script outlines two cases for factoring trinomials: Case One with a leading coefficient of one, and Case Two with a leading coefficient other than one.
- 🔢 The process for Case One involves multiplying the constant terms, listing factors of the result, and finding the pair that sums to the middle coefficient.
- 🔄 For Case Two, the process is more involved, requiring multiplication of the leading coefficient and the constant term, listing factors, and then using group factoring to find the solution.
- 📑 The speaker provides notes for pre-algebra, algebra 1, geometry, algebra 2, and trigonometry, which can be useful for studying after mastering the basics.
- 🔑 The script mentions that there are no shortcuts for learning mathematics, but there are tips and tricks to make certain tasks more manageable.
- 📈 The video aims to give hope and a clear method to students struggling with factoring, encouraging them to seek help and practice to overcome difficulties.
Q & A
What is the main topic discussed in the video script?
-The main topic discussed in the video script is factoring, specifically focusing on factoring trinomials in algebra.
Why do students often struggle with factoring trinomials?
-Students often struggle with factoring trinomials because it can be confusing when they first learn algebra or factoring, and it requires a specific procedure to master.
What is the importance of factoring in algebra?
-Factoring is one of the most critical skills in algebra, as it is necessary for success in various algebraic situations and is essential for passing algebra courses.
What is the name of the online math help program mentioned in the script?
-The online math help program mentioned in the script is called TabletClass Math.
Who is the founder of TabletClass Math and what is his role?
-The founder of TabletClass Math is John, who is also a middle and high school math teacher and has created an online program to help students with math.
What types of math courses does the TabletClass Math program offer?
-The TabletClass Math program offers over 100 different math courses ranging from pre-algebra, algebra 1, geometry, algebra 2, trigonometry, to pre-calculus, as well as test preparation courses for various exams.
What is the significance of note-taking in learning mathematics according to the script?
-According to the script, note-taking is crucial in learning mathematics as it helps students stay focused and engaged with the material, and successful math students almost always have great math notes.
What are the two cases of trinomials mentioned in the script?
-The two cases of trinomials mentioned in the script are Case 1, where the leading coefficient is 1, and Case 2, where the leading coefficient is not 1.
What is the first step in factoring trinomials as described in the script?
-The first step in factoring trinomials as described in the script is to multiply the leading coefficient by the constant term to find the product.
What is the purpose of listing out the factors of the constant term in the factoring process?
-The purpose of listing out the factors of the constant term is to find pairs of factors that add up to the middle coefficient of the trinomial, which is essential for determining the correct factors to use in the factoring process.
What technique is used in Case 2 of factoring trinomials that is different from Case 1?
-In Case 2 of factoring trinomials, after finding the correct pairs of factors, the technique of group factoring is used, where the greatest common factor is factored out from groups of terms.
What is the final advice given in the script for students struggling with factoring?
-The final advice given in the script for students struggling with factoring is to learn and follow the provided procedures, which are described as bulletproof and effective for factoring trinomials, and to seek help and practice to improve their skills.
Outlines
📚 Introduction to Factoring Trinomials
The speaker, John, introduces the topic of factoring trinomials, a common challenge for students learning algebra. He reassures students that confusion is natural when learning something new and emphasizes the importance of mastering factoring as a critical skill for success in algebra. John offers an alternative method for factoring trinomials that students can use if they are struggling with their current approach. He also introduces himself as the founder of TabletClass Math and a middle/high school math teacher, mentioning his extensive online math help program that covers a wide range of courses and test preparation materials. John stresses the importance of note-taking and being fully engaged in the learning process, without distractions like cell phones.
🔍 Understanding Factoring Techniques
This section delves into the specifics of factoring, starting with the importance of identifying and factoring out the greatest common factor (GCF) from expressions. The speaker then focuses on trinomials, distinguishing between two cases based on the leading coefficient. Case one involves trinomials with a leading coefficient of one, which are generally easier to factor. Case two, which will be discussed later, involves trinomials with a leading coefficient other than one. The speaker also mentions special factoring rules like the difference of squares and group factoring, which are essential skills for algebra. He encourages students to strengthen their factoring abilities for overall success in algebra, offering additional resources and courses for those who need more help.
📝 Step-by-Step Factoring of Case One Trinomials
The speaker provides a detailed walkthrough of how to factor trinomials in case one, where the leading term has a coefficient of one. He outlines a three-step process: multiplying the constant terms, listing the factors of the product, and finding the pair of factors that sum up to the middle term's coefficient. Using the example of a trinomial with a constant term of -6, he demonstrates how to identify the correct pair of factors that add up to the middle term's coefficient, which in this case is 1. The speaker emphasizes that practice will make this process easier and assures students that this methodical approach will yield the correct factors if the trinomial is factorable.
🔑 Advanced Factoring: Case Two Trinomials
The speaker moves on to case two trinomials, which have a leading coefficient other than one, making them more complex to factor. He uses the example of a trinomial with a leading coefficient of 6 and a constant term of -24, guiding the audience through the process of multiplying the leading coefficient by the constant term, listing the factors of the result, and identifying the pair of factors that add up to the middle term's coefficient. The speaker then introduces group factoring, where the greatest common factor is factored out from groups of terms, leading to the final factored form. He acknowledges that this method may seem confusing at first but assures students that it is a reliable technique that will work for both case one and case two trinomials if they are factorable.
🚀 Overcoming Factoring Challenges
In the concluding paragraph, the speaker reinforces the message that there is always a way to overcome difficulties in mathematics, including factoring trinomials. He encourages students to try the techniques he has presented and to seek help when needed, emphasizing that it's okay to struggle and that additional resources are available. The speaker also invites students to subscribe to his YouTube channel for more math content and to consider his Math Health program for comprehensive math support. He ends with well-wishes for the students' mathematical journeys and a reminder that with effort and the right approach, anyone can succeed in mathematics.
Mindmap
Keywords
💡Factoring
💡Trinomial
💡Greatest Common Factor (GCF)
💡Special Factoring Rules
💡Case One
💡Case Two
💡Group Factoring
💡Note-Taking
💡Prime Polynomial
💡Mastery
Highlights
The video discusses factoring trinomials, a common challenge for students learning algebra.
John, the founder of TabletClass Math, introduces himself and his online math help program.
The importance of mastering factoring as a critical skill for success in algebra is emphasized.
Different approaches to factoring trinomials are presented, including a suggested method for students struggling with the concept.
The necessity of understanding the greatest common factor in factoring is highlighted.
Two types of trinomials, 'Case One' and 'Case Two', are introduced with different factoring techniques.
The video provides a step-by-step guide for factoring trinomials in 'Case One' scenarios.
The concept of prime polynomials is explained, comparing them to prime numbers in arithmetic.
The importance of note-taking in learning mathematics is stressed, with a call to put away distractions like cell phones.
A detailed walkthrough of the factoring process for 'Case Two' trinomials is presented.
The technique of group factoring is introduced to handle more complex trinomials in 'Case Two'.
The video offers reassurance that difficulties in factoring can be overcome with practice and the right techniques.
The presenter encourages viewers to take initiative in seeking help for their math struggles, leveraging free resources available online.
The video concludes with a reminder that mastering factoring is essential for all types of algebra problems.
A call to action for viewers to subscribe to the channel for more math help and tutorials.
The presenter shares his belief that no one should fail mathematics and encourages viewers to take responsibility for their learning.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: