Man Throws Rock Projectile Motion Problem

that physics tutor
7 Aug 202314:49
EducationalLearning
32 Likes 10 Comments

TLDRIn this educational video, the host tackles problem 3.21 from Young and Friedman's 'University Physics' textbook, involving projectile motion. A man throws a rock from a 15-meter building at 30 m/s, 33 degrees above horizontal. The host aims to find the maximum height above the roof, the speed just before impact, and the horizontal range. Using kinematic equations, the host calculates the maximum height as 13.62 meters, the speed before hitting the ground as 34.55 m/s, and the horizontal range as approximately 103 meters. The video is designed to help viewers understand projectile motion and solve physics problems with a hands-on approach.

Takeaways
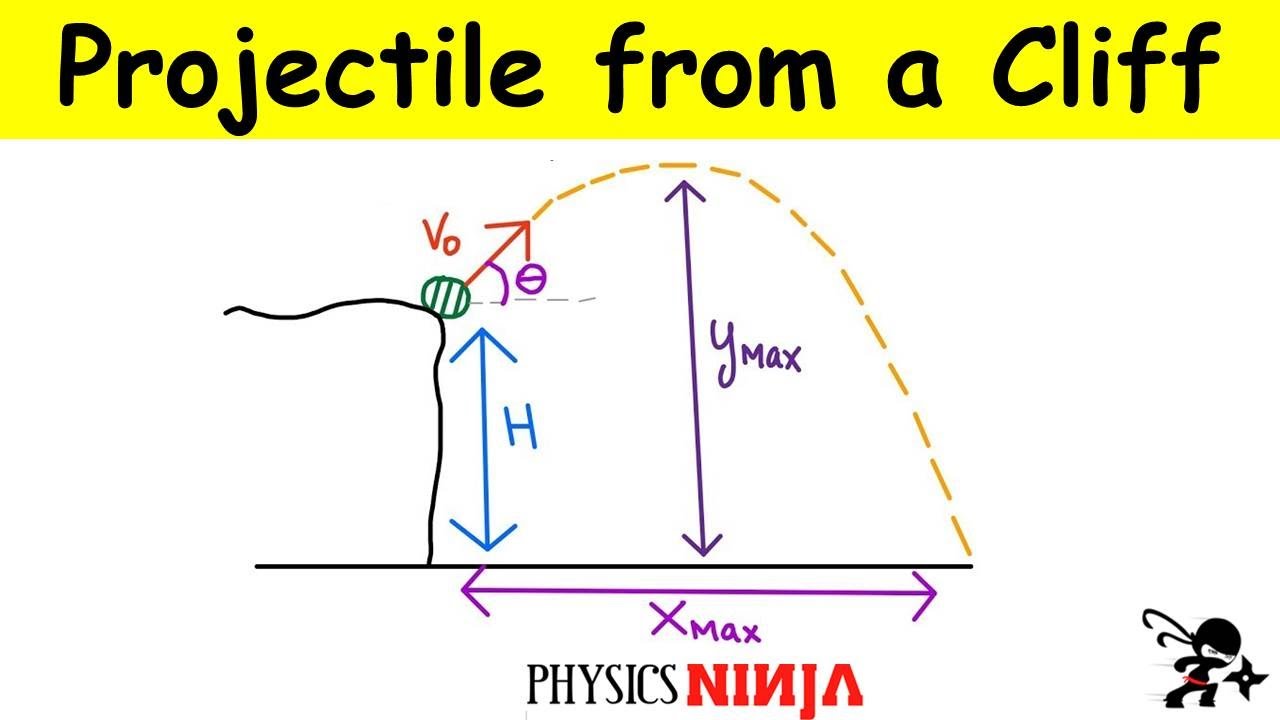
  • 🧍‍♂️ A man stands on a 15-meter tall building and throws a rock at 30 meters per second at an angle of 33 degrees above the horizontal.
  • 📏 The problem requires calculating the maximum height above the roof the rock reaches, the speed just before it hits the ground, and the horizontal range from the base of the building to where the rock strikes the ground.
  • 🖼️ A diagram is drawn to visualize the building's height and the rock's trajectory.
  • 🔢 The initial vertical component of the velocity is calculated as 30 * sin(33) meters per second.
  • 📉 At the maximum height, the vertical velocity is 0 meters per second. Using kinematic equations, the maximum height above the roof is found to be 13.62 meters.
  • 🏋️‍♀️ For part B, the speed of the rock just before it hits the ground is calculated by considering both vertical and horizontal components of the velocity.
  • 💨 The horizontal component of the velocity remains constant throughout the motion as there is no horizontal acceleration.
  • ⚡ The final vertical speed just before impact is calculated as 23.68 meters per second, and the total speed combining both components is 34.55 meters per second.
  • 🕒 To find the horizontal range, the time of flight is determined by solving for the time the rock remains in the air, calculated to be approximately 4.08 seconds.
  • 🏃‍♂️ Finally, using the horizontal velocity and the time of flight, the horizontal range is calculated to be 103 meters.
Q & A

  • What is the problem described in the video script?

    -The problem involves a man standing on the roof of a 15-meter tall building and throwing a rock with a speed of 30 meters per second at an angle of 33 degrees above the horizontal. The task is to calculate the maximum height above the roof the rock reaches, the speed of the rock just before it strikes the ground, and the horizontal range from the base of the building to where the rock lands.

  • What is the initial speed of the rock thrown by the man?

    -The initial speed of the rock is 30 meters per second.

  • At what angle is the rock thrown relative to the horizontal?

    -The rock is thrown at an angle of 33 degrees above the horizontal.

  • What is the height of the building from which the rock is thrown?

    -The building is 15 meters tall.

  • What is the first part of the problem asking for?

    -The first part of the problem asks for the maximum height (D1) above the roof that the rock reaches.

  • What is the formula used to calculate the maximum height the rock reaches?

    -The formula used to calculate the maximum height is derived from the kinematic equation: V_f^2 = V_i^2 + 2ad, where V_f is the final velocity (which is 0 at the maximum height), V_i is the initial velocity, a is the acceleration due to gravity, and d is the displacement (the maximum height in this case).

  • What is the calculated maximum height above the roof that the rock reaches?

    -The calculated maximum height above the roof is 13.62 meters.

  • What is the second part of the problem asking for?

    -The second part of the problem asks for the speed of the rock (VF) just before it strikes the ground.

  • What is the final speed of the rock just before it strikes the ground?

    -The final speed of the rock just before it strikes the ground is calculated to be 34.55 meters per second.

  • What is the third part of the problem asking for?

    -The third part of the problem asks for the horizontal range (DX) from the base of the building to the point where the rock lands.

  • How is the horizontal range calculated?

    -The horizontal range is calculated by multiplying the horizontal component of the initial velocity (VX) by the time of flight (T), which is determined by solving for the time it takes for the rock to fall the vertical distance (minus 15 meters in this case).

  • What is the calculated horizontal range from the base of the building to where the rock lands?

    -The calculated horizontal range is approximately 103 meters.

  • What is the significance of the Pythagorean theorem in this problem?

    -The Pythagorean theorem is used to calculate the resultant velocity (VF) of the rock just before it strikes the ground by combining the horizontal (VFX) and vertical (VFY) components of the velocity.

  • Why is air resistance ignored in this problem?

    -Air resistance is ignored to simplify the problem, allowing for the use of basic projectile motion equations without the need to account for the effects of air resistance on the rock's trajectory and speed.

  • How does the video script guide the viewer through solving the problem?

    -The video script guides the viewer by breaking down the problem into parts, drawing a diagram, writing down known values, selecting appropriate kinematic equations, and step-by-step solving for the unknowns such as maximum height, final velocity, and horizontal range.

Outlines
00:00
📚 Projectile Motion Problem Introduction

The video begins with the presenter introducing a physics problem from Young and Friedman's 'University Physics' textbook. The problem involves a man throwing a rock from the roof of a 15-meter tall building with an initial speed of 30 meters per second at an angle of 33 degrees above the horizontal. The goal is to calculate the maximum height the rock reaches above the roof, the speed of the rock just before it hits the ground, and the horizontal range from the base of the building to where the rock lands. The presenter suggests starting by visualizing the problem and understanding the projectile motion, which involves both vertical and horizontal components of motion.

05:03
🧭 Calculating Maximum Height and Final Speed

In this segment, the presenter focuses on solving for the maximum height above the roof the rock reaches and its speed just before impact. Using kinematic equations, specifically the formula relating final velocity squared to initial velocity, acceleration, and displacement (VF^2 = VI^2 + 2ad), the presenter calculates the maximum height to be 13.62 meters above the roof. The presenter then moves on to determine the rock's speed before it hits the ground, taking into account both the vertical and horizontal components of the motion. The vertical component's final velocity is found using the same kinematic equation, and the horizontal component's velocity remains constant due to the absence of horizontal acceleration. The presenter uses the Pythagorean theorem to find the resultant velocity, which is approximately 34.55 meters per second.

10:03
📏 Determining Horizontal Range of Projectile

The final part of the video addresses the calculation of the horizontal range, which is the distance from the base of the building to where the rock lands. The presenter first determines the time of flight by using the vertical motion kinematic equations, finding a time of approximately 4.08 seconds. With the time of flight and the horizontal velocity component (30 meters per second times cosine of 33 degrees), the presenter calculates the horizontal range using the formula DX = VX * T. The resulting horizontal range is approximately 103 meters. The presenter concludes by inviting feedback on the video format and encourages viewers to like and subscribe for more content.

Mindmap
Keywords
💡Projectile Motion
Projectile motion refers to the motion of an object thrown or projected into the air, which moves along a curved path under the action of gravity. In the video, the concept is central as it explains how a rock thrown at an angle from a building follows a parabolic trajectory. The rock's motion is broken down into vertical and horizontal components, which are analyzed separately to determine the maximum height, speed at impact, and horizontal range.
💡Velocity
Velocity is a vector quantity that refers to the rate of change of an object's position with respect to time, including both magnitude (speed) and direction. In the script, the initial velocity of the rock is given as 30 meters per second at a 33-degree angle above the horizontal. The velocity is crucial in calculating the rock's trajectory and is used to determine both the vertical and horizontal components of its motion.
💡Angle of Projection
The angle of projection is the angle at which an object is launched into the air. In the context of the video, the rock is thrown at a 33-degree angle to the horizontal, which influences the trajectory and the time the rock spends in the air. The angle is used to decompose the initial velocity into its vertical and horizontal components.
💡Acceleration Due to Gravity
Acceleration due to gravity is the acceleration that an object experiences when it falls freely under the influence of gravity, which is approximately 9.8 meters per second squared on Earth. In the video, this acceleration is used to calculate the changes in the rock's vertical velocity and to determine when it will reach its maximum height and when it will hit the ground.
💡Maximum Height
Maximum height is the highest point reached by an object in projectile motion above its initial launching point. The script discusses calculating the maximum height the rock reaches above the building's roof using the kinematic equations, which is essential for understanding the total distance the rock travels vertically.
💡Horizontal Range
Horizontal range is the total horizontal distance an object in projectile motion travels from its launch point to its landing point. The video aims to find the horizontal range from the base of the building to where the rock lands, which involves calculating the time the rock is in the air and its horizontal velocity.
💡Kinematic Equations
Kinematic equations are mathematical formulas used to describe the motion of an object. In the script, these equations are used to relate the initial and final velocities, acceleration, time, and displacement of the rock. They are essential tools for solving the problem and finding the required quantities such as maximum height, speed at impact, and horizontal range.
💡Speed at Impact
Speed at impact is the velocity of an object just before it hits a surface or another object. The video script calculates the speed of the rock just before it strikes the ground by considering both the vertical and horizontal components of its velocity at that moment, using the Pythagorean theorem to find the resultant velocity.
💡Vertical Component
The vertical component of velocity or displacement is the component of an object's motion that is perpendicular to the horizontal plane. In the video, the vertical component is used to determine the maximum height the rock reaches and its speed at impact in the vertical direction, which is affected by gravity.
💡Horizontal Component
The horizontal component of velocity or displacement is the component of an object's motion that is parallel to the horizontal plane. The script explains that the horizontal component of the rock's velocity remains constant throughout its flight because there is no acceleration in the horizontal direction, and it is used to calculate the horizontal range.
💡Pythagorean Theorem
The Pythagorean theorem is a principle in geometry that states that in a right-angled triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the other two sides. In the context of the video, the theorem is used to calculate the resultant velocity of the rock just before it hits the ground by combining its vertical and horizontal components.
Highlights

Problem 3.21 from Young and Friedman's University Physics textbook involves a man throwing a rock from a 15-meter tall building.

The rock is thrown at a speed of 30 meters per second at an angle of 33 degrees above the horizontal.

Air resistance is ignored in the calculations.

The goal is to calculate the maximum height above the roof the rock reaches, its speed before hitting the ground, and the horizontal range.

A kinematic approach is used to solve the problem, focusing on the vertical and horizontal components of motion.

At the maximum height, the vertical component of the rock's velocity is zero.

The maximum height above the roof (D1) is calculated to be 13.62 meters using the kinematic equation.

For the speed of the rock before it hits the ground (VF), both vertical and horizontal components must be considered.

The vertical component of the final velocity (VFy) is calculated using the kinematic equation, resulting in 23.68 m/s.

The horizontal component of the velocity (Vx) remains constant throughout the motion due to no acceleration in the x-direction.

The horizontal range is dependent on the time the rock is in the air, which is calculated from the vertical motion.

The time of flight (T) is determined to be approximately 4.08 seconds using the vertical motion kinematics.

The horizontal range (DX) is then calculated by multiplying the horizontal velocity (Vx) by the time of flight (T).

The final horizontal range is found to be approximately 103 meters.

The video provides a step-by-step solution to a physics problem involving projectile motion.

The importance of understanding both the vertical and horizontal components of projectile motion is emphasized.

The video concludes with a call to action for viewers to like, subscribe, and provide feedback on the content.

Transcripts

Browse More Related Video

Win the Prize Projectile Motion Problem

AP Physics B Kinematics Presentation General Problems #12

Projectile launched off a cliff at an angle

Projectile Motion Example - How fast when it hits the ground

Two Dimensional Motion Problems - Physics

University Physics Leaping the River II Problem

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Projectile MotionPhysics ProblemMaximum HeightHorizontal RangeKinematic EquationsYoung and FriedmanUniversity PhysicsProblem SolvingEducational ContentScience Tutorial