AP Calculus AB - Straight Line Motion

Mr. Ayton
3 Aug 202011:38
EducationalLearning
32 Likes 10 Comments

TLDRThe video script delves into the physics of straight-line motion, focusing on the relationship between position, velocity, and acceleration over time. It begins with a position-time graph, illustrating an object starting at a positive four meters and moving to 2.8 meters in about 1.2 seconds. The object's motion is characterized by a backward movement, a stop, and then a forward progression. The velocity, derived from the position function, is shown to transition from negative to zero and then to positive, indicating a change in direction. The acceleration, as the second derivative of the position function, is determined to be a linear function. The script emphasizes understanding the direction of motion and the concept that velocity is a vector quantity with direction, while speed is a scalar. Finally, the script applies these principles to calculate the velocity and acceleration of a particle at specific time points, using derivatives to analyze the motion and direction of the particle's movement.

Takeaways
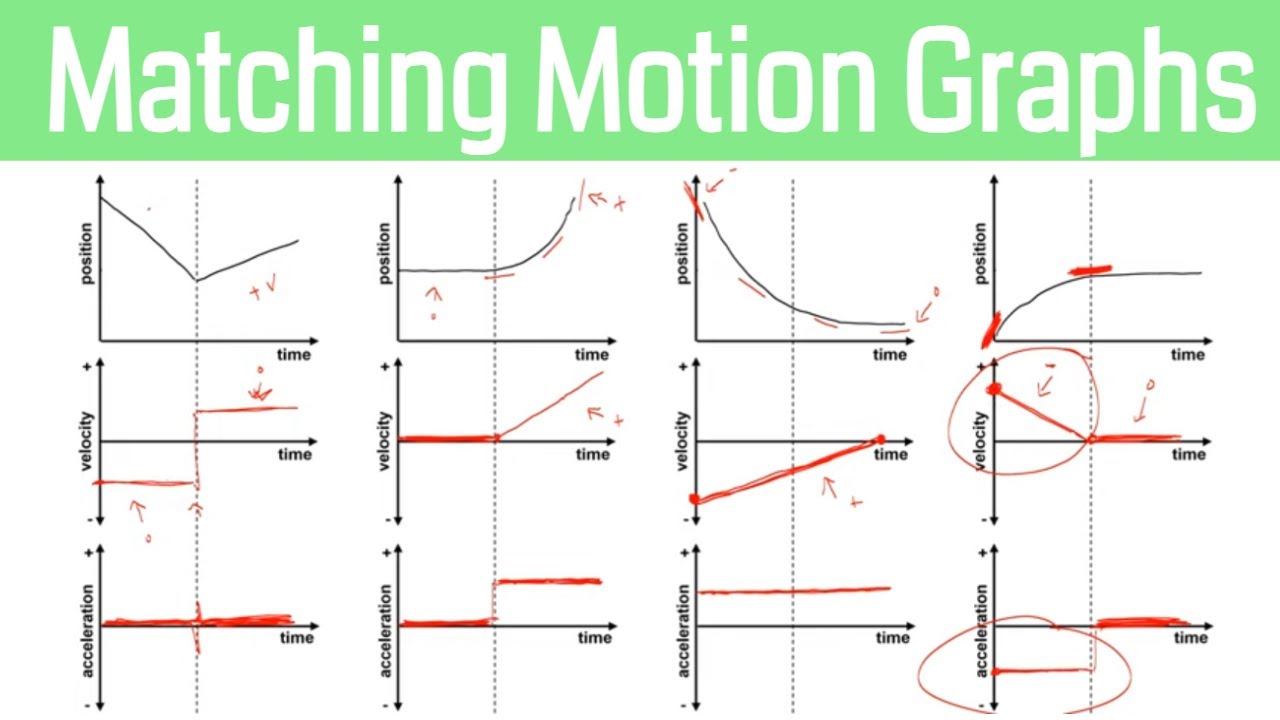
  • 📍 The position-time graph represents an object's position with respect to time, with the x-axis for time and the y-axis for position in meters.
  • 🔄 An object's motion can be analyzed by observing changes in its position over time, indicating whether it's moving forward or backward.
  • 📈 Velocity, the rate of change of position with respect to time, is derived from the position function and can be represented graphically to show direction and speed changes.
  • ⏹ A velocity of zero indicates that the object is momentarily at rest before changing direction.
  • 🚀 Acceleration is the rate of change of velocity with respect to time, obtained by taking the second derivative of the position function.
  • ↗️ When the velocity-time graph shows a transition from negative to positive, it signifies a change in the direction of motion from backward to forward.
  • 📉 Negative velocity indicates the object is moving in the reverse direction, while positive velocity means it's moving forward.
  • 🏃 Speed is a scalar quantity that only considers magnitude, whereas velocity is a vector quantity that includes both magnitude and direction.
  • 📊 The shape of the position, velocity, and acceleration graphs can be used to interpret the motion of an object over time, with each successive derivative representing a different aspect of motion.
  • ⏳ At any given instant, the slope of the tangent on the position-time graph represents the instantaneous velocity, and the slope of the tangent on the velocity-time graph represents the instantaneous acceleration.
  • 🔢 To find the velocity or acceleration at a specific time, substitute that time into the derived velocity or acceleration function, respectively.
Q & A

  • What is the initial position of the object in the given physics example?

    -The initial position of the object is at positive 4 meters away from the reference point.

  • What does it mean when the position-time graph of an object shows a decrease in position from 4 meters to 2.8 meters?

    -It means the object is moving backwards, as the position is decreasing over time.

  • What is the relationship between velocity and position with respect to time in the context of the script?

    -Velocity is the derivative of the position function with respect to time, which means it represents the rate of change of position at any given time.

  • How does the velocity-time graph indicate the direction of motion of the object?

    -A negative velocity indicates the object is moving backwards, a velocity of zero indicates the object is momentarily at rest, and a positive velocity indicates the object is moving forwards.

  • What is the difference between speed and velocity?

    -Speed is a scalar quantity that refers to the magnitude of motion, while velocity is a vector quantity that includes both the magnitude and direction of motion.

  • How does the acceleration function relate to the velocity function?

    -Acceleration is the derivative of the velocity function with respect to time, indicating the rate of change of velocity.

  • What is the significance of the acceleration being a linear function in the script?

    -The linear nature of the acceleration function implies that the rate of change of velocity is constant over time, which is typical in scenarios with constant forces applied.

  • What does it mean when the acceleration is negative?

    -A negative acceleration means that the object is decelerating, or its velocity is decreasing over time.

  • At what value does the velocity of the object become zero according to the script?

    -The velocity of the object becomes zero at approximately 1.2 seconds, indicating the object momentarily stops before changing direction.

  • How can one determine the particle's velocity at a specific time using the position function?

    -One can determine the particle's velocity at a specific time by taking the derivative of the position function and then evaluating it at the desired time.

  • What is the particle's velocity at time equals two seconds in the example provided?

    -The particle's velocity at time equals two seconds is negative one meter per second, indicating the particle is moving to the left.

  • How can the direction of the particle's motion be inferred from the velocity value?

    -If the velocity value is negative, the particle is moving in the negative direction (to the left if considering the x-axis), and if it's positive, the particle is moving in the positive direction (to the right on the x-axis).

Outlines
00:00
📈 Understanding Position, Velocity, and Acceleration in Physics

The first paragraph introduces the concept of straight-line motion in physics, focusing on the position function with respect to time. It explains how the position-time graph can be used to determine the movement of an object, including its direction and speed. The velocity, which is the derivative of the position function, is discussed in detail, showing how it can be negative (indicating backward movement) or positive (forward movement). The paragraph also covers how acceleration, the second derivative of the position function, can be calculated and interpreted. It provides an example of how to find the velocity and acceleration at specific points in time using derivatives.

05:00
📊 Interpreting Graphs of Motion: Position, Velocity, and Acceleration

The second paragraph delves into interpreting graphs of motion, emphasizing the importance of understanding whether a graph represents position, velocity, or acceleration over time. It explains how to read the graphs to determine the direction and speed of an object's movement. The paragraph illustrates how the slope of the tangent on a velocity-time graph indicates the acceleration at a particular instant. It also discusses how to find the velocity and acceleration at specific times by taking derivatives of the position and velocity functions, respectively.

10:02
🚀 Applying Derivatives to Analyze Straight-Line Motion

The third paragraph continues the discussion on straight-line motion, focusing on the application of derivatives to analyze an object's movement. It describes how the direction of motion and the particle's speed can be determined from the velocity and acceleration. The paragraph provides an example calculation to find the velocity and acceleration at specific times, highlighting the process of taking derivatives. It concludes by emphasizing the simplicity of the process, which involves taking derivatives to transition from position to velocity to acceleration.

Mindmap
Keywords
💡Position function
A position function is a mathematical representation that describes the position of an object with respect to time. In the context of the video, it is used to plot the object's movement on a graph with the x-axis representing time in seconds and the y-axis representing position in meters. The position function starts at +4 meters and changes over time, indicating the object's movement.
💡Velocity
Velocity is a vector quantity that refers to the rate of change of an object's position with respect to time. It indicates both the speed and direction of the object's motion. In the video, the velocity is derived from the position function and is represented on a graph showing how the object's velocity changes from negative (moving backwards) to zero (stopped) and then to positive (moving forwards).
💡Acceleration
Acceleration is the rate of change of velocity with respect to time. It is a vector quantity that indicates how quickly the velocity of an object is changing, and it can be positive (speeding up), negative (slowing down), or zero (constant speed). The script explains how to find acceleration by taking the derivative of the velocity function, resulting in a linear function that shows the object's changing velocity over time.
💡Derivative
In calculus, a derivative represents the rate at which a function is changing at a certain point. It is used to find the slope of the tangent line to a curve at a given point, which corresponds to the instantaneous velocity or acceleration. The video demonstrates taking derivatives of the position function to find velocity and then taking the derivative of the velocity function to find acceleration.
💡Power rule
The power rule is a basic theorem in calculus that allows for the differentiation of polynomial functions. It states that the derivative of x^n, where n is a constant, is n*x^(n-1). In the video, the power rule is used to find the derivatives of the position and velocity functions, which are polynomials.
💡Tangent slope
The slope of the tangent to a curve at a particular point is the instantaneous rate of change of the function at that point. In the context of the video, the slope of the tangent to the position-time graph represents the velocity at a specific time, and the slope of the tangent to the velocity-time graph represents the acceleration.
💡Scalar vs. Vector
A scalar quantity has only magnitude, while a vector quantity has both magnitude and direction. Speed is a scalar because it only describes how fast an object is moving, regardless of direction. Velocity, on the other hand, is a vector because it includes information about the direction of motion. The video emphasizes the difference between speed and velocity, particularly when discussing the object's movement.
💡
💡Direction of motion
The direction of motion refers to the path or way in which an object is moving. In the video, the direction is inferred from the sign of the velocity and acceleration values. Positive values indicate movement in the positive direction (usually to the right in a graph), while negative values indicate movement in the opposite direction.
💡Instantaneous point
An instantaneous point in time refers to a specific moment during which the velocity or acceleration is being measured. The video discusses the object's velocity and acceleration at particular instants, such as at time equals two seconds or three seconds, to understand the exact state of motion at those moments.
💡Cubic function
A cubic function is a type of polynomial function of degree three. In the video, the position function is described as a cubic function, which means it has the form f(x) = ax^3 + bx^2 + cx + d. The cubic nature of the function allows for complex movements, such as changes in direction and varying speeds, which are explored in the context of the object's motion.
💡Quadratic function
A quadratic function is a polynomial function of degree two. After differentiating the position function, the resulting velocity function is a quadratic function. This function helps in understanding how the velocity changes over time, which is essential for analyzing the object's acceleration and direction of motion.
Highlights

Introduction to physics applications in AP Calculus AB focusing on straight-line motion.

Explanation of position function with respect to time, using a graph with position on the x-axis and time on the y-axis.

Demonstration of an object moving backwards and then forwards, shown through changes in the position-time graph.

Derivation of velocity with respect to time as the change in position over time, using the power rule.

Interpretation of the velocity graph, including the significance of negative velocity indicating backward motion.

Differentiation between speed and velocity, emphasizing that velocity is a vector quantity with direction.

Calculation of acceleration as the second derivative of the position function with respect to time.

Graphical representation of how acceleration changes from negative to positive, indicating a change in direction.

Identification of when an object has stopped by the velocity being zero, as shown on the velocity-time graph.

Explanation of how a velocity-time graph can indicate whether an object is moving forward or backward.

Use of derivatives to transition from position to velocity to acceleration in the context of straight-line motion.

Example calculation of a particle's velocity at a specific time using the derived velocity function.

Determination of a particle's acceleration at a given time by differentiating the velocity function.

Analysis of the direction of a particle's motion based on the sign of its velocity.

Calculation of a particle's speed and its implications on the velocity and acceleration.

Comprehensive overview of the physics of straight-line motion using calculus derivatives.

Transcripts

Browse More Related Video

AP Physics B Kinematics Presentation #81

Worked example: Motion problems with derivatives | AP Calculus AB | Khan Academy

Motion problems: when a particle is speeding up | AP Calculus AB | Khan Academy

AP Physics 1 review of 1D motion

Calculus - Position Average Velocity Acceleration - Distance & Displacement - Derivatives & Limits

How to Match Motion Graphs in Physics

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
PhysicsMotionCalculusStraight-LinePosition FunctionVelocityAccelerationDerivativesVector QuantityScalar QuantityPhysics EducationAP CalculusMotion Analysis