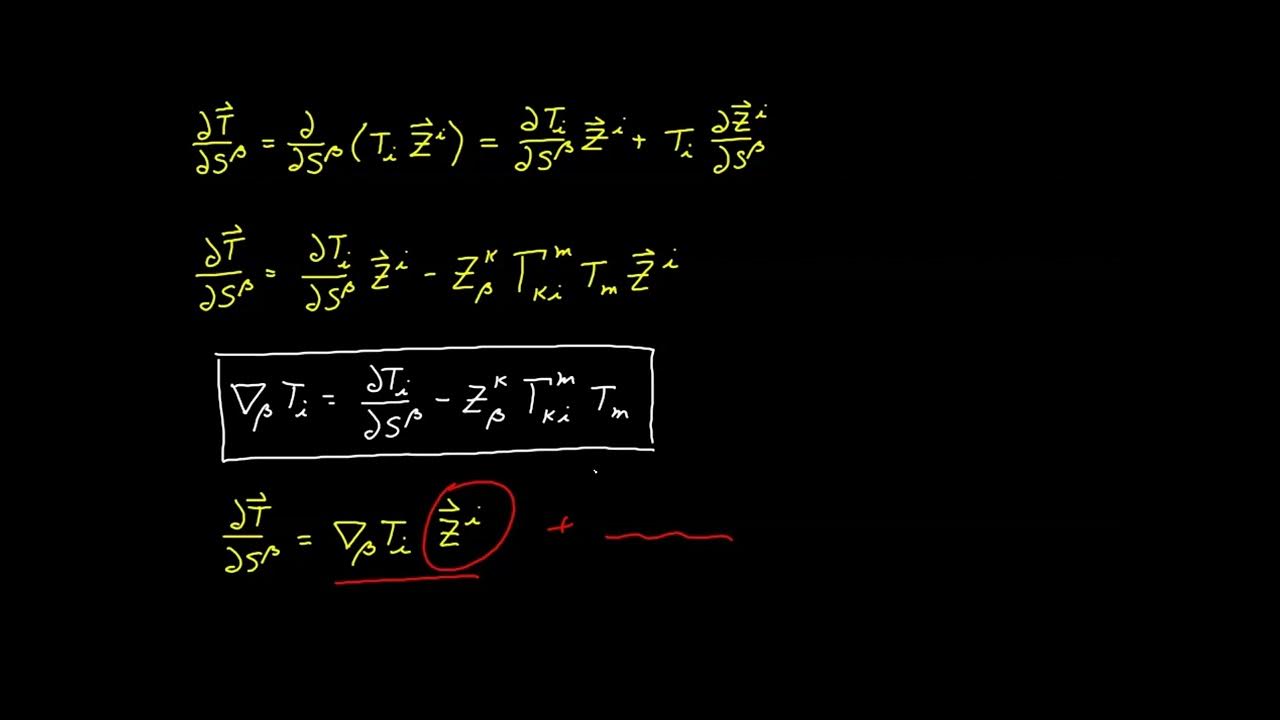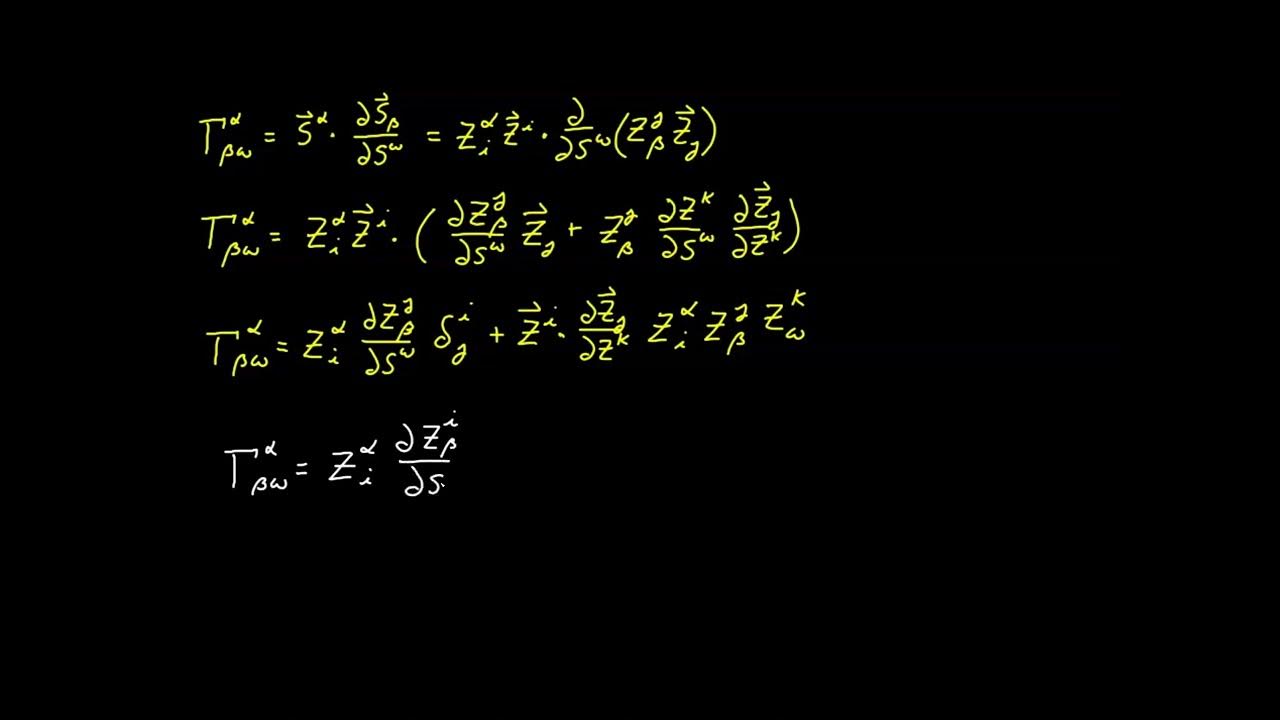Video 60 - Shift Tensor

Tensor Calculus

5 Jun 202222:51

EducationalLearning

32 Likes 10 Comments

TLDRThis video introduces the concept of the shift tensor in tensor calculus, essential for transitioning between surface and ambient perspectives on submanifolds. The shift tensor, a unique mixed tensor with both surface and ambient indices, is defined through partial derivatives of ambient coordinates relative to surface coordinates. The video explores its properties, including its transformation rules and the ability to invert its form. It also demonstrates how the shift tensor allows for the conversion of basis vectors and vector components between the two coordinate systems, with a focus on vectors within the tangent plane, setting the stage for further exploration in subsequent videos.

Takeaways

📚 The video introduces the concept of the shift tensor, a unique object in submanifolds that facilitates the transition between surface and ambient perspectives.
🔍 The shift tensor is defined as the partial derivative of ambient coordinates with respect to surface coordinates, creating a 'mixed' tensor with both ambient and surface indices.
📏 The shift tensor, when represented as a matrix, has three rows and two columns, totaling six components, reflecting its ability to map between different coordinate systems.
🔄 The video demonstrates the transformation rule for the shift tensor, proving its tensorial nature through the application of the quotient theorem and the chain rule of differentiation.
🔄 The transformation of the shift tensor involves Jacobian factors that correspond to the type of index being transformed, confirming its status as a tensor.
🔄 The video shows how to invert the shift tensor by simultaneously lowering the ambient index and raising the surface index, creating what is referred to as the inverse of the shift tensor.
🔗 The contraction of the shift tensor and its inverse with the ambient index yields the Kronecker delta function, a key relationship in tensor calculus.
📈 The script explains how to shift vector components between the ambient and surface perspectives using the shift tensor, which is crucial for understanding the relationship between different coordinate systems.
📉 The video emphasizes that the ability to shift between perspectives is predicated on the vector lying in the tangent plane, with more general cases to be discussed in future videos.
🧠 The script concludes with a recap of the key points, reinforcing the understanding of the shift tensor's role in tensor calculus and its applications in submanifolds.

Q & A

What is the shift tensor in the context of tensor calculus?
-The shift tensor is a mathematical object unique to submanifolds in tensor calculus. It provides a convenient way to shift between the surface and ambient perspectives in a mathematical space.
How is the shift tensor related to the position vector in the script?
-The shift tensor is derived from the position vector's expression in terms of both surface coordinates (s) and ambient coordinates (z). It is used to construct a composite function involving partial derivatives of the position vector with respect to these coordinates.
What is the significance of the composite function involving partial derivatives in the script?
-The composite function is used to derive the shift tensor. It involves taking partial derivatives of the position vector with respect to both surface and ambient coordinates, which leads to the definition of the shift tensor.
What is the structure of the shift tensor in terms of indices?
-The shift tensor has a unique structure with a surface index (alpha) and an ambient index (i). It combines the use of both types of indices, making it a 'mixed tensor' with a total of six components.
Why is the shift tensor referred to as a 'mixed tensor' in the script?
-The term 'mixed tensor' is used because the shift tensor combines both surface and ambient indices in its definition. This mixing of index types is not common in standard tensor definitions.
How does the script demonstrate that the shift tensor is indeed a tensor?
-The script uses the quotient theorem and the transformation rule to prove that the shift tensor behaves as a tensor. It shows that the shift tensor transforms correctly under coordinate transformations, maintaining its tensorial properties.
What is the transformation rule derived for the shift tensor in the script?
-The transformation rule for the shift tensor involves a chain rule differentiation that includes partial derivatives with respect to both the primed and unprimed coordinate systems. It demonstrates how the shift tensor components transform under a change of coordinates.
How does the script show the inversion of the shift tensor?
-The script shows the inversion of the shift tensor by simultaneously lowering the ambient index and raising the surface index. This is achieved through contraction with the ambient and surface metric tensors, respectively.
What is the relationship between the shift tensor and the delta function in the script?
-The script demonstrates that a contraction of the shift tensor with its inverse, when contracted along the ambient index, results in the Kronecker delta function. This relationship is crucial for understanding the tensor's properties.
How does the script use the shift tensor to relate vector components in the ambient and surface perspectives?
-The script shows that by contracting the shift tensor with vector components, one can convert between the components as expressed in the ambient space and those in the surface space. This conversion is valid for vectors lying in the tangent plane of the surface.
What is the practical application of the shift tensor as described in the script?
-The practical application of the shift tensor is to facilitate the transition between the ambient and surface perspectives in tensor calculus. It allows for the analysis of vectors and other tensorial quantities in both coordinate systems, which is essential for studying submanifolds.

Outlines

00:00

📚 Introduction to the Shift Tensor

This paragraph introduces the concept of the shift tensor, a unique object in submanifolds that facilitates the transition between surface and ambient perspectives in tensor calculus. The shift tensor is defined through the partial derivative of the position vector with respect to surface and ambient coordinates. The structure of the tensor is explained, highlighting its 'mixed' nature due to the combination of surface and ambient indices. The paragraph also discusses the tensor's matrix representation and its six components, emphasizing the shift tensor's role in expressing position vectors and covariant basis vectors in both coordinate systems.

05:02

🔍 Derivation and Transformation of the Shift Tensor

The second paragraph delves into the derivation of the shift tensor's transformation rule. By applying the chain rule to the partial derivatives, the transformation of the shift tensor under a change of coordinates is established. The process involves the use of Jacobians for both ambient and surface coordinates, proving the tensorial nature of the shift tensor. The paragraph also explains how to lower and raise indices of the tensor, resulting in its inverse form, and demonstrates the tensor's transformation properties through the quotient theorem.

10:06

🔗 Contraction of Shift Tensor and its Inverse

This section explores the contraction of the shift tensor with its inverse, leading to the discovery of important relationships between the tensor and its components. The contraction along the ambient index is shown to result in a Kronecker delta function, which is a key property of the tensor. The paragraph also discusses the implications of this contraction for the basis vectors in both ambient and surface coordinate systems, highlighting the tensor's utility in transforming between these systems.

15:07

🚀 Vector Representation in Ambient and Surface Perspectives

The fourth paragraph examines how a vector lying in the tangent plane can be represented using both the surface and ambient basis vectors. By employing the shift tensor, the vector components in the surface perspective are related to those in the ambient perspective. The paragraph demonstrates how the shift tensor allows for the conversion of vector components between the two coordinate systems, emphasizing the tensor's role in facilitating this transformation.

20:08

🔚 Recap and Application of Shift Tensor Principles

The final paragraph provides a comprehensive recap of the entire video's content, summarizing the key points and concepts related to the shift tensor. It reiterates the definition, transformation rules, and the process of inverting the shift tensor. The paragraph also revisits the tensor's ability to transition between ambient and surface perspectives, setting the stage for future videos that will apply these principles to specific sample surfaces.

Mindmap

Keywords

💡Shift Tensor

The shift tensor is a mathematical object unique to submanifolds in tensor calculus, introduced in the video to facilitate the transition between surface and ambient coordinate systems. It is defined as the partial derivative of ambient coordinates with respect to surface coordinates, and it plays a crucial role in the video's theme of understanding the relationship between these two perspectives. For instance, the script describes the shift tensor as having six components, arranged in a matrix with three rows and two columns, which is essential for the manipulation and transformation of coordinates.

💡Submanifold

A submanifold is a concept in differential geometry where a lower-dimensional manifold is embedded within a higher-dimensional space. In the context of the video, the shift tensor is specifically defined for submanifolds, indicating that the discussion is about how to handle geometrical objects that are not just points in space but have an intrinsic curvature or structure. The video does not directly define 'submanifold,' but it is implied through the use of the shift tensor.

💡Surface Coordinates (s)

Surface coordinates, denoted by 's' in the script, are the parameters used to describe points on a surface within a higher-dimensional space. They are essential for defining the position vector 'r' as a function of these coordinates. The video emphasizes the importance of surface coordinates in constructing the shift tensor, as they are the basis for differentiating and transforming between surface and ambient perspectives.

💡Ambient Coordinates (z)

Ambient coordinates, represented by 'z', are the parameters of the larger space in which a submanifold is embedded. The video discusses how these coordinates can also be expressed as functions of the surface coordinates 's', and they are integral to the construction of the composite function and the chain rule application when deriving the shift tensor.

💡Composite Function

A composite function in the context of the video refers to the combination of the position vector 'r' expressed in terms of both surface coordinates 's' and ambient coordinates 'z'. The script uses the concept of a composite function to derive the shift tensor by taking partial derivatives of 'r' with respect to 's' and 'z', illustrating the interconnectedness of surface and ambient coordinate systems.

💡Partial Derivative

Partial derivatives are used in the video to differentiate a function with respect to one variable while keeping all other variables constant. The script specifically mentions taking the partial derivative of the position vector 'r' with respect to the surface coordinate 's' and the ambient coordinate 'z', which is foundational in defining the shift tensor.

💡Covariate Basis Vectors

Covariate basis vectors, both surface and ambient, are vectors that form the basis of the tangent space at a point on a manifold. The video discusses how these vectors are used in the derivation of the shift tensor and how they relate to the surface and ambient coordinates. They are essential for understanding the local structure of the manifold and its embedding space.

💡Mixed Tensor

A mixed tensor, as mentioned in the script, is a tensor that has both upper (contravariant) and lower (covariant) indices. The shift tensor is referred to as a mixed tensor because it combines the use of a surface index with an ambient index. The script explains that this combination is unique and allows for the tensor to have a non-square matrix representation with six components.

💡Jacobian

The Jacobian matrix, derived in the video, is a matrix of all first-order partial derivatives of a vector-valued function. The script uses the Jacobian to describe the transformation rules for the shift tensor, showing how it changes under a coordinate transformation. It is crucial for proving that the shift tensor is indeed a tensor and for understanding how it transforms between coordinate systems.

💡Tensor Transformation Rule

The tensor transformation rule discussed in the video outlines how a tensor changes when switching between different coordinate systems. The script derives this rule for the shift tensor, showing that it maintains its tensorial properties under transformation, which is confirmed by the presence of Jacobian factors associated with each index.

💡Contravariant and Covariant Basis Vectors

Contravariant and covariant basis vectors are used in tensor calculus to describe the basis of tangent spaces in a coordinate system. The video script explains how these basis vectors relate to the shift tensor and how they can be used to express vectors in both surface and ambient perspectives. The dot product of these basis vectors with the shift tensor is used to derive important relationships within the video.

Highlights

Introduction of the shift tensor, a unique object to submanifolds that facilitates movement between surface and ambient perspectives.

Expression of position vector as a function of both surface and ambient coordinates, establishing a composite function for further analysis.

Derivation of the shift tensor through partial derivatives, emphasizing its role as a mixed tensor with both surface and ambient indices.

The shift tensor's unique structure as a matrix with three rows and two columns, differing from traditional square matrices.

Identification of the shift tensor as a mixed tensor due to the combination of surface and ambient index types.

Demonstration of the shift tensor's properties using the quotient theorem, affirming its status as a tensor.

Derivation of the transformation rule for the shift tensor, showcasing its behavior under coordinate transformations.

Proof of the shift tensor's tensorial nature through the application of the chain rule in differentiation.

Inversion of the shift tensor by lowering the ambient index and raising the surface index, creating a new tensor relationship.

Formation of a tensor equation that allows for the shifting of basis vectors from ambient to surface perspectives.

Dot product analysis between the contour and covariant basis vectors, leading to an important relationship involving the shift tensor.

Expression of a vector in the tangent plane using both surface and ambient basis vectors, facilitated by the shift tensor.

Derivation of relationships to shift vector components between ambient and surface perspectives using the shift tensor.

Explanation of the shift tensor's utility in transitioning between ambient and surface perspectives for vectors in the tangent plane.

Recap of the video's content, summarizing the shift tensor's definition, properties, and its role in transforming between coordinate systems.

Transcripts

Browse More Related Video

Video 72 - Surface Covariant Derivative for Non Tangent Vectors

Video 65 - Tangent Space Transformations

Video 58 - Tangent Space

Video 70 - Surface Christoffel Examples

Video 69 - Christoffel Symbol for Surfaces - Part 2

Video 88 - Embedded Curves - Part 1

Related Tags

Tensor Calculus Shift Tensor Submanifolds Surface Coordinates Ambient Coordinates Partial Derivatives Composite Function Covariate Basis Mixed Tensor Jacobian Matrix Vector Components