Video 71 - Surface Covariant Derivative for Tangent Vectors

Tensor Calculus

5 Jun 202224:17

EducationalLearning

32 Likes 10 Comments

TLDRIn this video, the covariant derivative is explored in the context of surface manifolds, focusing on vectors within the tangent plane. The script explains how the covariant derivative's definition remains consistent with Euclidean spaces but introduces an additional term when applied to curved surfaces, reflecting both surface and normal projections. Two key exceptions in curved surfaces are highlighted: the loss of the metronomic property for basis vectors and the non-commutativity of the covariant derivative, which will be used to measure intrinsic curvature. The video promises to extend the analysis to vectors outside the tangent plane in the subsequent installment.

Takeaways

📚 The video discusses the covariant derivative in the context of surface manifolds, specifically focusing on vectors within the tangent plane.
🔍 Initially, the analysis is restricted to vectors in the tangent plane, with the intention to extend to more general cases in subsequent videos.
📉 The covariant derivative is defined as the partial derivative of a vector with respect to a surface coordinate, under the stipulation that the vector lies in the tangent plane.
📈 The script uses the product rule to expand the expression for the covariant derivative and introduces the concept of surface covariant derivative.
🔄 The covariant derivative's definition remains consistent with the Euclidean space even when applied to curved surfaces, but its application requires adjustments due to the curvature.
📐 The video highlights the importance of the curvature tensor, which affects how the covariant derivative behaves on a curved surface, introducing components in both the tangent and normal directions.
🔑 The script explains that the covariant derivative of basis vectors on a curved surface does not possess the metronomic property, unlike in Euclidean space.
🔄 It is noted that the covariant derivative is not commutative on curved surfaces, which is a significant departure from its behavior in flat spaces.
🔍 The video emphasizes that while most properties of the covariant derivative carry over from Euclidean spaces to curved surfaces, the loss of metronomic property and commutativity are key exceptions.
🔗 The non-commutativity of the covariant derivative on curved surfaces is linked to the intrinsic curvature of the space, which will be explored further in later videos.
📝 The script concludes by reinforcing that the general results derived are inclusive of the special case of flat surfaces, where the curvature tensor equals zero and the metronomic property is restored.

Q & A

What is the main focus of the video script?
-The video script focuses on the analysis of the covariant derivative in relation to surface manifolds, specifically for vectors that lie in the tangent plane.
What was the starting point of the discussion in the script?
-The discussion began with the covariant derivative introduced in video 28, where the partial derivative of a vector with respect to a coordinate was taken.
What is the significance of restricting the discussion to vectors in the tangent plane?
-Restricting the discussion to vectors in the tangent plane allows for the simplification of the analysis and the investigation of the covariant derivative in a more controlled environment before extending to more general cases.
How is vector 't' represented in the context of the script?
-Vector 't' is represented as a linear combination using surface coordinates, expressed as 't^α * s_α', which is only possible if the tensor or vector lies in the tangent plane.
What mathematical operation is used to expand and distribute the factor 't^α'?
-The product rule is used to expand and distribute the factor 't^α' into the terms derived from the partial derivative of the basis vector with respect to the coordinate.
What is the result of taking the partial derivative of a vector with respect to a surface coordinate?
-The result is a new expression that includes the surface covariant derivative of 't^α' times the basis vector 's_α', plus an additional term involving 't^α' and the curvature tensor.
How does the definition of the surface covariant derivative for vectors in the tangent plane compare to the standard covariant derivative?
-The definition of the surface covariant derivative for vectors in the tangent plane is exactly the same as the standard covariant derivative used in Euclidean spaces.
What property of the covariant derivative is lost when dealing with curved surfaces?
-The metronomic property of the basis vectors is lost, meaning that the covariant derivative of the basis vectors on curved surfaces is not equal to zero.
What is the implication of the covariant derivative not being commutative on curved surfaces?
-The non-commutativity of the covariant derivative on curved surfaces implies that the order in which the derivatives are taken matters, which can be used to quantify the intrinsic curvature of the space.
How does the video script conclude the discussion on the covariant derivative for surface manifolds?
-The script concludes by summarizing that while the definition of the covariant derivative remains the same for vectors in the tangent plane, there are adjustments needed when applying it as part of the operation for finding the partial derivative of a vector on a curved surface, and it highlights the two exceptions to the properties of the covariant derivative in curved spaces.

Outlines

00:00

📚 Introduction to Covariant Derivative on Surface Manifolds

This paragraph introduces the concept of the covariant derivative in the context of surface manifolds. It explains that the discussion will initially focus on vectors within the tangent plane, with a subsequent extension to more general cases. The covariant derivative is explored by taking the partial derivative of a vector with respect to surface coordinates, and it is stipulated that the vector lies in the tangent plane. The vector is expressed as a linear combination of surface coordinates, and the product rule is applied to derive the covariant derivative. The paragraph also references previous videos for the derivation of the basis vector's partial derivative with respect to the coordinate.

05:02

🔍 Analysis of Covariant Derivative for Tangent Vectors

The second paragraph delves into the specifics of the covariant derivative for vectors that lie in the tangent plane. It discusses the similarity between the surface covariant derivative and the standard covariant derivative, highlighting that no adjustments are needed for the definition when dealing with tangent vectors. The paragraph also addresses the implications of taking the partial derivative, which introduces a component in the normal direction. The result is a vector that may point in any direction, not just within the tangent plane. The special case of a plane, where the curvature tensor is zero, is also mentioned, showing that the general expression simplifies to the known result for a plane.

10:03

📘 Covariant Derivative for Contravariant and Covariant Vector Components

This paragraph extends the analysis of the covariant derivative to include both contravariant and covariant vector components. It goes through the process of applying the product rule and making substitutions based on previous derivations. The paragraph then defines the surface covariant derivative for a covariant vector component and expresses the partial derivative in terms of this new definition. The summary also points out that the properties derived for Euclidean spaces carry over to curved surfaces, with the exception of two important properties that are different in surface geometry.

15:04

🚫 Loss of Metronymic Property and Commutativity on Curved Surfaces

The fourth paragraph discusses the loss of two important properties of the covariant derivative when applied to curved surfaces. It explains that the metronymic property, which states that the covariant derivative of basis vectors is zero in Euclidean space, does not hold on curved surfaces. The paragraph also addresses the loss of commutativity of the covariant derivative, meaning that the order in which the derivatives are taken matters on curved surfaces. This non-commutativity is a key aspect for understanding the intrinsic curvature of the space.

20:07

🔚 Conclusion: Covariant Derivative on Curved Surfaces and Its Implications

The final paragraph concludes the video by summarizing the main points discussed. It emphasizes that the definition of the covariant derivative remains the same for vectors in the tangent plane on curved surfaces, but adjustments are necessary when taking the partial derivative due to the introduction of a normal projection. The paragraph reiterates the two exceptions discussed earlier: the loss of the metronymic property for basis vectors and the loss of commutativity of the covariant derivative. It also mentions that these general results include the flat plane as a special case and looks forward to extending the analysis to vectors not in the tangent plane in the next video.

Mindmap

Keywords

💡Covariant Derivative

The covariant derivative is a concept in differential geometry that generalizes the notion of the derivative to curved spaces. It allows for the differentiation of vector fields and other tensors in a way that is consistent with the curvature of the space. In the video, the covariant derivative is discussed in the context of surface manifolds, specifically for vectors that lie in the tangent plane. The script explores how the covariant derivative is calculated and how it differs when applied to flat versus curved spaces, highlighting its importance in understanding the intrinsic properties of manifolds.

💡Tangent Plane

A tangent plane is a concept from calculus and differential geometry that refers to a flat surface that touches a curve or surface at a single point. In the context of the video, the tangent plane is the local approximation of the surface at a given point, and the analysis is initially restricted to vectors that lie within this plane. The script discusses how the covariant derivative of a vector field is calculated when the field is confined to the tangent plane, setting the stage for a deeper exploration of the properties of tensors on curved surfaces.

💡Surface Manifolds

A surface manifold is a topological space that locally resembles a Euclidean space but may have a global structure that is curved or otherwise non-Euclidean. The video focuses on the analysis of the covariant derivative in the context of surface manifolds, which are two-dimensional spaces embedded within a higher-dimensional space. The script explains how the covariant derivative is applied to vectors on these manifolds and how the results differ from those in flat spaces due to the curvature of the surface.

💡Partial Derivative

A partial derivative is a derivative of a function of multiple variables with respect to one of those variables, while the others are held constant. In the video, the partial derivative is used in the calculation of the covariant derivative for vectors on a surface manifold. The script illustrates how taking the partial derivative of a vector field with respect to a surface coordinate can result in a vector that has both a surface and a normal projection, indicating the influence of the manifold's curvature.

💡Basis Vector

A basis vector is a vector that is used to define a coordinate system in a vector space. In differential geometry, basis vectors are often used to express other vectors in the space as linear combinations. The video script discusses basis vectors in the context of surface manifolds, explaining how the covariant derivative of these vectors is not zero on curved surfaces, which is a departure from their behavior in flat spaces.

💡Curvature Tensor

The curvature tensor is a mathematical object that encodes the intrinsic curvature of a space or a surface within a higher-dimensional space. It is a key concept in the study of differential geometry and general relativity. In the video, the curvature tensor is mentioned in the context of how it affects the calculation of the covariant derivative and how it can be used to distinguish between flat and curved spaces.

💡Metric Tensor

The metric tensor is a fundamental concept in differential geometry that provides a way to measure distances and angles in a curved space. It is used to define the inner product of vectors in the tangent space at each point of the manifold. The video script mentions the metric tensor in the context of its properties being preserved under the covariant derivative operation on curved surfaces, unlike the basis vectors.

💡Levy-Civita Symbol

The Levy-Civita symbol, also known as the permutation symbol, is a mathematical tool used in tensor analysis, particularly in the context of the covariant derivative and curvature. It is a tensor that has specific symmetries and is used to simplify expressions involving indices. The video script discusses how the properties of the Levy-Civita symbol remain consistent under the covariant derivative operation on curved surfaces.

💡Metronomic Property

The metronomic property refers to the characteristic of certain tensors, such as basis vectors in Euclidean spaces, to have a covariant derivative equal to zero. This property simplifies calculations involving these tensors. The video script explains how this property does not hold for basis vectors on curved surfaces, leading to more complex expressions when taking covariant derivatives.

💡Intrinsic Curvature

Intrinsic curvature is a measure of the curvature of a space or surface that is independent of any embedding in a higher-dimensional space. It is a fundamental concept in differential geometry and is related to the curvature tensor. The video script hints at the use of the non-commutativity of the covariant derivative to quantify the intrinsic curvature of a space, which is a key aspect of the study of curved manifolds.

Highlights

Introduction of the covariant derivative in the context of surface manifolds, specifically for vectors within the tangent plane.

Restriction of the analysis to tensors lying in the tangent plane, with an extension to more general cases in subsequent videos.

Representation of vector t as a linear combination using surface coordinates, exclusive to vectors in the tangent plane.

Use of the product rule to expand the covariant derivative expression and the incorporation of results from previous videos.

Substitution of expressions derived in videos 68 and 69 to simplify the covariant derivative analysis for surface coordinates.

Reordering and renaming of indexes to facilitate the factoring out of the basis vector s alpha.

Definition of the surface covariant derivative for vectors in the tangent plane, paralleling the standard covariant derivative form.

Identification of the surface covariant derivative's similarity to the standard covariant derivative, with adjustments for curved surfaces.

Explanation of the partial derivative's normal and surface projections when dealing with curved surfaces.

Preservation of the covariant derivative definition for vectors in the tangent plane, with modifications for application on curved surfaces.

Analysis of the covariant derivative for contravariant vector components, using a linear combination with a contravariant basis.

Determination of the surface covariant derivative for covariant components, maintaining the form from Euclidean spaces.

Discussion on the loss of the metronomic property for basis vectors on curved surfaces, contrasting with Euclidean spaces.

Revelation of the non-commutative nature of the surface covariant derivative on curved surfaces, differing from flat spaces.

Retaining of metronomic properties for metric tensors, delta factors, and Levy-Civita symbols in curved surfaces.

Generalization of results for curved surfaces, with special cases for planes as curvature tensor equals zero.

Upcoming extension of analysis to vectors not lying in the tangent plane in subsequent videos.

Transcripts

Browse More Related Video

Tensor Calculus Lecture 8: Embedded Surfaces and the Curvature Tensor

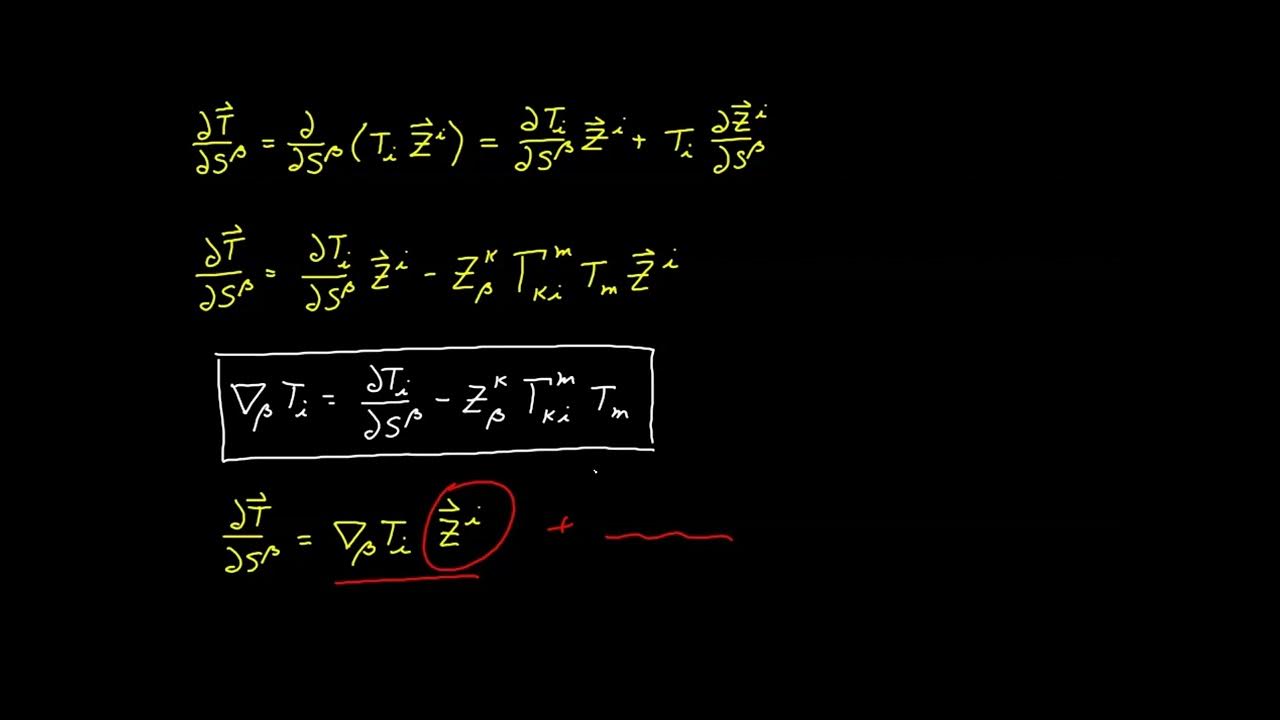
Video 72 - Surface Covariant Derivative for Non Tangent Vectors

Video 89 - Curve Projections

Video 73 - Surface Covariant Derivative Properties

Tensor Calculus 17: The Covariant Derivative (flat space)

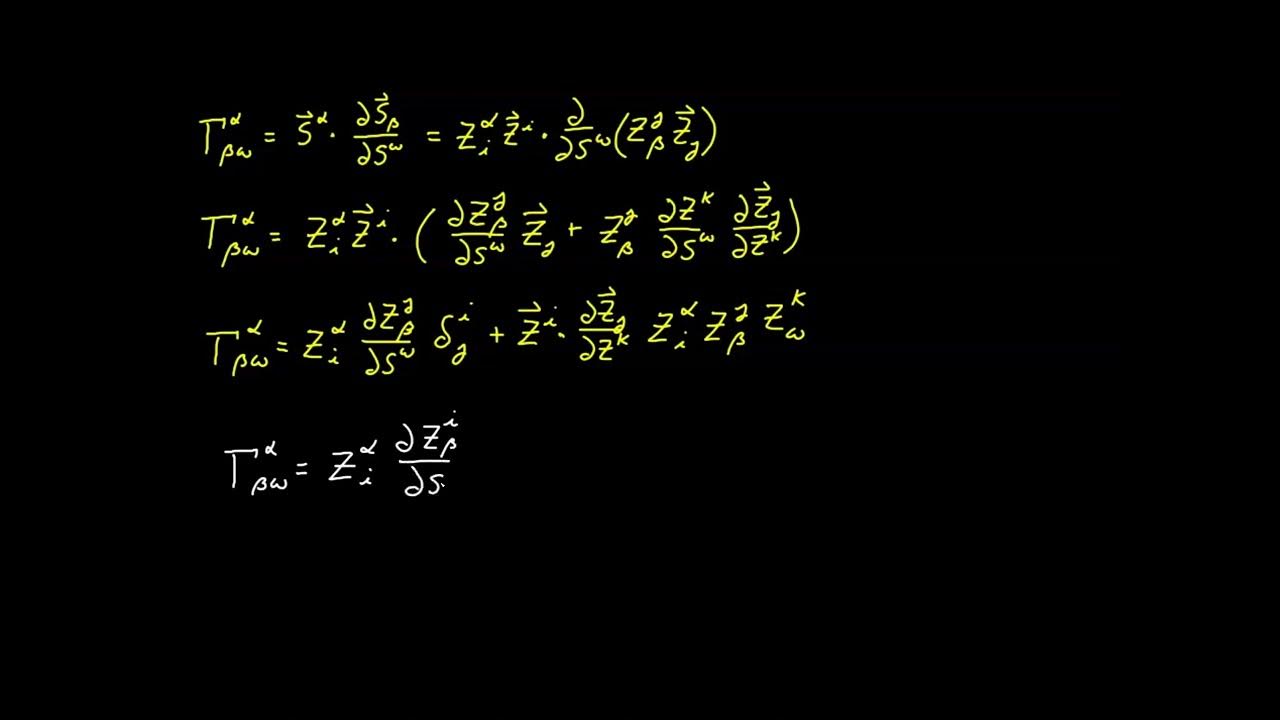
Video 69 - Christoffel Symbol for Surfaces - Part 2

Related Tags

Tensor Calculus Covariant Derivative Surface Manifolds Partial Derivative Tangent Plane Basis Vectors Metric Tensors Curved Surfaces Euclidean Space Intrinsic Curvature