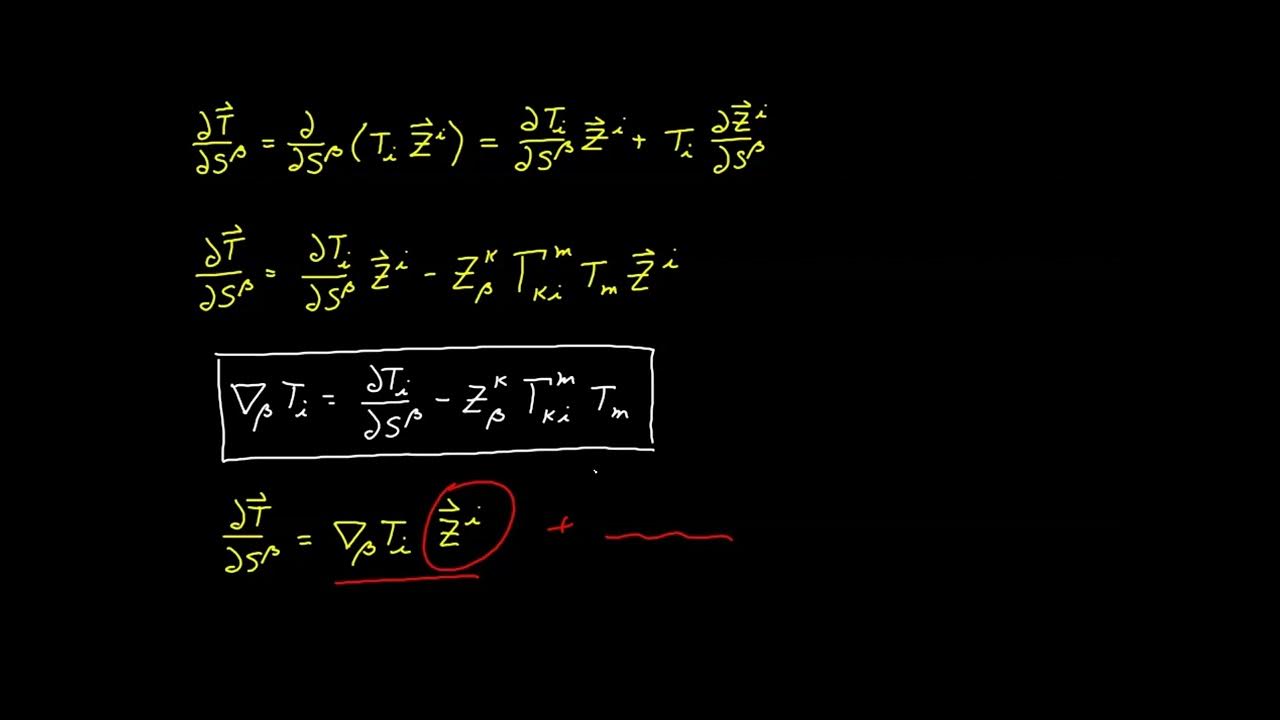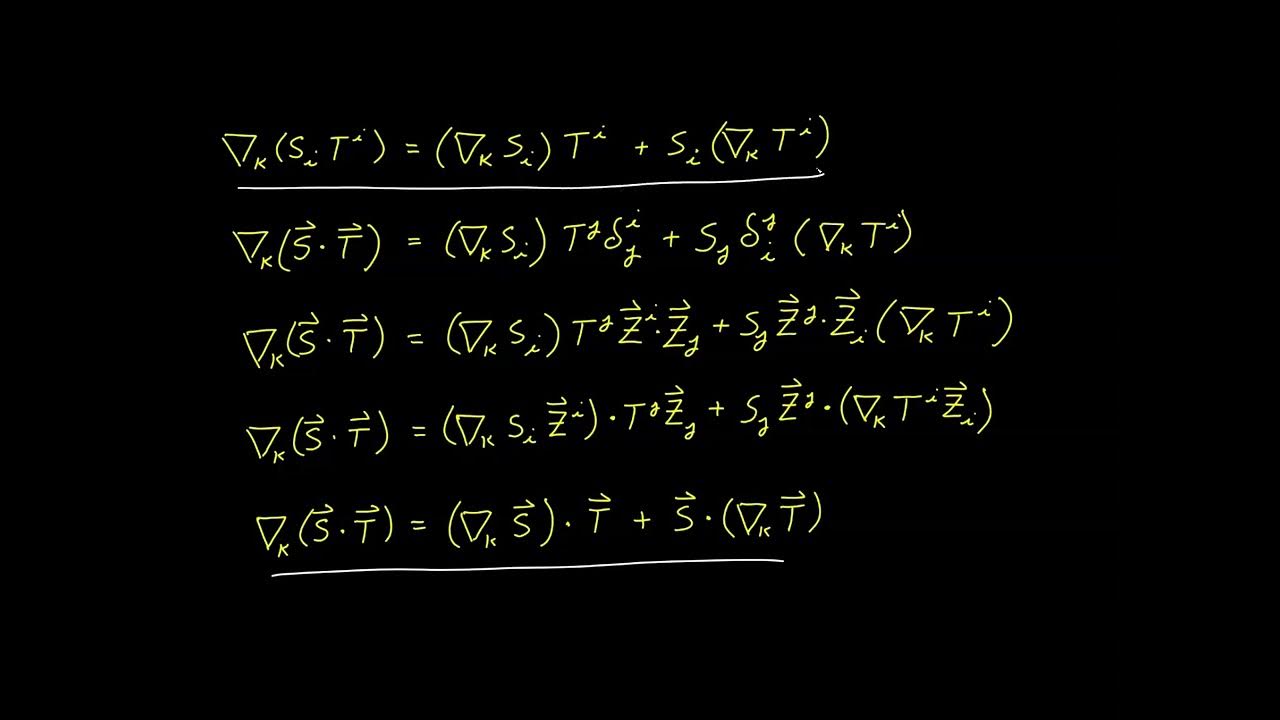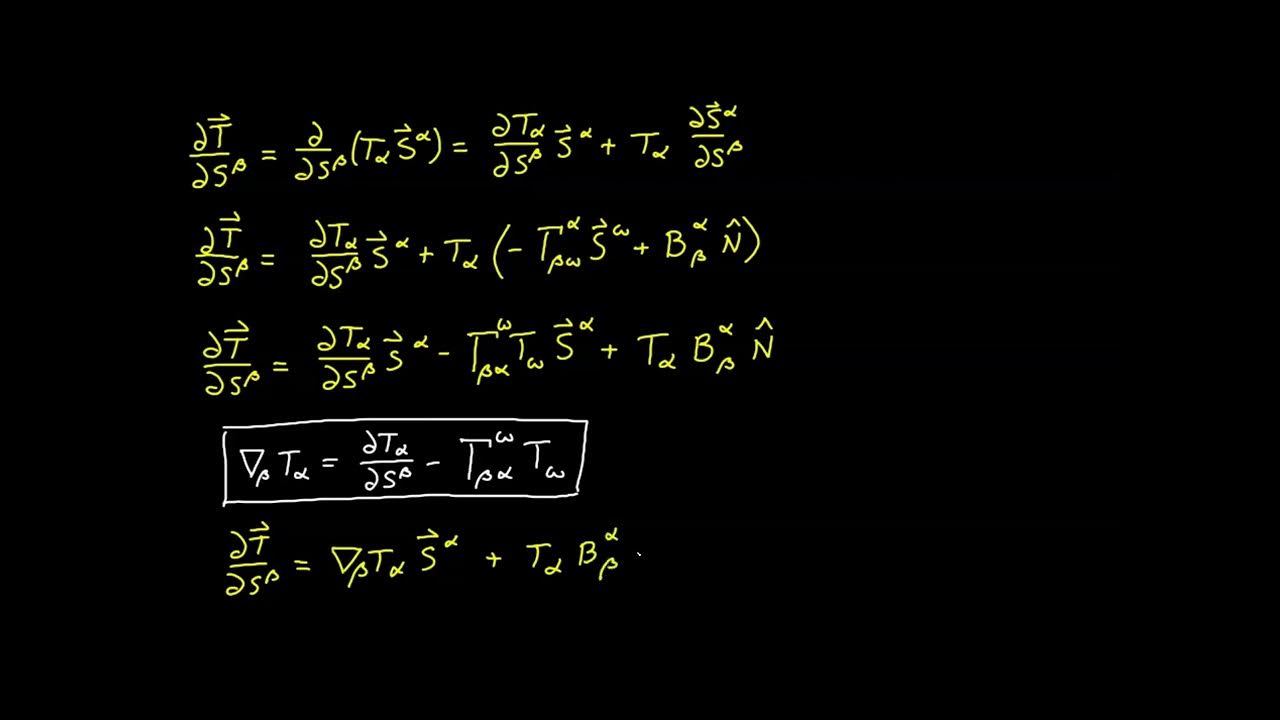Video 73 - Surface Covariant Derivative Properties
TLDRIn this video, the series on tensor calculus concludes with a review of the surface covariant derivative's properties. The script revisits the basic definitions and universal applicability of these derivatives, highlighting the linearity of the operation and the product rule. It also covers the process for finding the covariant derivative of tensors of any rank, emphasizing the consistency of index structures. The video further explores the metronomic property, the chain rule relating surface and normal covariant derivatives, and introduces surface contravariant derivatives, divergence, gradient, directional derivatives, and the Laplacian. The script concludes by demonstrating how these concepts apply to sample curved surfaces, reinforcing the continuity of tensor calculus principles from Euclidean to curved spaces.
Takeaways
- 📚 The video concludes the study of the surface covariant derivative by reviewing its properties, both modified and unmodified, in comparison to the covariant derivative from previous videos.
- 🔍 There are four basic forms of the surface covariant derivative, two applicable only to vectors in the tangent plane and two universally applicable to any vector.
- 📉 The partial derivative representation also has four different forms, with two restricted to tangent vectors and two that can be used universally.
- 🔄 The covariant derivative of a curved manifold requires additional terms to account for results not lying in the tangent plane, involving normal projections.
- 📈 Most properties of the normal covariant derivative apply to the surface covariant derivative as well, with some exceptions already discussed.
- 📝 The sum rule for the covariant derivative, allowing for the linear operation of derivative taking, is applicable to the surface covariant derivative regardless of index types.
- 📚 The product rule for tensors, where the derivative of a product is the product of the derivative and the original tensor plus the original tensor times the derivative, is also applicable to surface covariant derivatives.
- 🔑 The process for finding the covariant derivative of a tensor of any rank can be applied to the surface covariant derivative, resulting in four different forms based on index types.
- 🔍 Contracted indexes do not affect the covariant derivative process, and the covariant derivative of a rank 0 tensor (scalar function) is simply its partial derivative.
- 🌐 The metronomic property holds for ambient basis vectors with respect to the surface covariant derivative, but not for surface basis vectors, unless the curvature tensor is zero (Euclidean space).
- 🔗 The surface covariant derivative is related to the normal covariant derivative through the shift tensor, provided the tensor is expressed in ambient indexes.
- 📐 Definitions for surface contravariant derivative, divergence, gradient, and Laplacian are provided, with the contravariant metric tensor being metronomic with respect to the surface covariant derivative.
- 📈 The Boss Vial formula for surface coordinates is the same as in Euclidean space, adapted for surface indexes to evaluate divergence or Laplacian.
- 🌐 The application of tensor calculus to curved surfaces is largely similar to that of Euclidean space, with tensor properties mostly carrying over with a few exceptions.
- 📊 The script ends with visual examples of gradient, divergence, and Laplacian for cylindrical and toroidal surfaces, without going through the calculations.
Q & A
What is the main focus of this video in the tensor calculus series?
-The main focus of this video is to review the properties of the surface covariant derivative, including properties that have been modified as well as those that remain unchanged from the covariant derivative discussed in earlier videos.
What are the four basic forms of the surface covariant derivative mentioned in the video?
-The four basic forms of the surface covariant derivative depend on whether the vector lies in the tangent plane or not. Two forms are used when the vector lies in the tangent plane, and the other two are universally applicable to any vector, whether it lies in the tangent plane or outside it.
Why are additional terms required in the definition of the surface covariant derivative for a curved manifold?
-Additional terms are required to account for the normal projection, which accommodates the fact that the result of the partial derivative may not lie in the tangent plane.
How does the sum rule apply to the surface covariant derivative?
-The sum rule states that the covariant derivative of a sum of tensors is equal to the sum of the covariant derivatives, and this rule applies to the surface covariant derivative just as it does for the normal covariant derivative.
What is the product rule in the context of the surface covariant derivative?
-The product rule for the surface covariant derivative states that the derivative of a product of tensors is equal to the derivative of the first tensor times the second tensor plus the first tensor times the derivative of the second tensor. This rule holds true regardless of the types of indexes involved.
What is the significance of contracted indexes in the surface covariant derivative?
-Contracted indexes do not participate in the process of finding the covariant derivative. For tensors of rank 0, such as scalars, the covariant derivative is simply the partial derivative, with no additional terms.
How does the metronylic property relate to the surface covariant derivative?
-The metronylic property holds for ambient basis vectors with respect to the surface covariant derivative, but not for surface basis vectors. However, if the curvature tensor is zero (as in a plane), the metronylic property is recovered for surface basis vectors.
What is the surface contravariant derivative, and how is it defined?
-The surface contravariant derivative is defined similarly to the contravariant derivative in earlier videos, using the contravariant metric tensor. It works because the contravariant metric tensor is metronylic with respect to the surface covariant derivative.
How is the surface Laplacian defined and used?
-The surface Laplacian is defined as the combination of the surface divergence and the surface gradient, contracted together. It operates similarly to the Laplacian defined in earlier videos, but it applies specifically to surface coordinates.
What does the video conclude about the application of tensor calculus to curved surfaces?
-The video concludes that most of the concepts and properties of tensor calculus for Euclidean space carry over to curved manifolds with only a few exceptions, and that curved surfaces can be treated as generalizations of planes.
Outlines
📚 Review of Surface Covariant Derivative Properties
This paragraph introduces the topic of the video, which is a comprehensive review of the properties of the surface covariant derivative in tensor calculus. The speaker mentions that while some properties require modification due to the introduction of new concepts, many others remain unchanged from the covariant derivative discussed in previous videos. The focus is on the four basic forms of the surface covariant derivative, applicable to vectors within or outside the tangent plane, and their corresponding partial derivatives. The paragraph also touches on the necessity of normal projection terms for curved manifolds to ensure the result of the partial derivative lies within the tangent plane. The speaker emphasizes that almost all properties from the covariant derivative carry over to the surface covariant derivative, with some exceptions already discussed.
🔍 Detailed Analysis of Surface Covariant Derivative Forms
The second paragraph delves into the process of deriving the surface covariant derivative for tensors of any rank, highlighting the four different forms that correspond to various types of indexes—upper, lower, surface, and ambient. The process involves taking the partial derivative and forming contractions based on the index positions. The paragraph explains the signs associated with upper and lower indexes and the use of Christoffel symbols for surface and ambient indexes. It also reiterates that contracted indexes do not participate in the covariant derivative process, which applies only to free indexes. The covariant derivative of a tensor of rank 0, or a scalar function, is simply its partial derivative. The paragraph concludes with the metronomic property, noting that while ambient basis vectors are metronomic with respect to the surface covariant derivative, surface basis vectors are not, except in the case of zero curvature, such as in a plane.
📘 Application of Tensor Calculus to Curved Manifolds
The final paragraph discusses the application of tensor calculus to curved manifolds, drawing parallels with Euclidean space and emphasizing the few exceptions that arise due to the curvature. The speaker defines the surface contravariant derivative and its relation to the metric tensor's metronomic property. The paragraph continues with definitions of the surface divergence, gradient, directional derivative, Laplacian, and the surface Boss-Vial formula, all of which are adapted from their Euclidean counterparts for use with surface coordinates. The speaker concludes by illustrating the gradient, divergence, and Laplacian for sample surfaces like the cylinder and torus, suggesting that viewers refer to previous videos for calculation techniques, and emphasizing the generalizability of tensor calculus principles from planes to curved surfaces.
Mindmap
Keywords
💡Tensor Calculus
💡Surface Covariant Derivative
💡Tangent Plane
💡Christoffel Symbols
💡Partial Derivative
💡Linear Operation
💡Product Rule
💡Metronomic Property
💡Surface Divergence
💡Surface Gradient
💡Surface Laplacian
Highlights
The video concludes the study of the surface covariant derivative by reviewing its properties.
Properties of the surface covariant derivative that do not require modification are discussed, which work as they did in previous videos.
Four basic forms for the surface covariant derivative are identified, with two forms universally applicable to any vectors.
The necessity of using surface indexes for vectors outside the tangent plane is explained.
The addition of normal projection terms for curved manifolds is discussed to accommodate tangent plane discrepancies.
Almost all properties of the normal covariant derivative apply to the surface covariant derivative, with some exceptions.
The sum rule for the covariant derivative of a sum of tensors is highlighted, emphasizing linearity.
The product rule is reiterated, showing no restrictions on the type of indexes involved.
A method for finding the covariant derivative of a tensor of any rank is presented, applicable to surface covariant derivatives.
The importance of free indexes in the covariant derivative process is underscored, with contracted indexes not participating.
The covariant derivative of a scalar function is shown to be equivalent to its partial derivative.
The metronomic property is explored, with ambient basis vectors being metronomic but surface basis vectors not.
An exception to the metronomic property is noted when the curvature tensor is zero, recovering the property in a Euclidean space.
The chain rule relating the surface covariant derivative to the normal covariant derivative via the shift tensor is introduced.
The definition of the surface contravariant derivative is provided, utilizing the metronilic contravariant metric tensor.
The surface divergence is defined, using a vector in the tangent plane and contracting surface indexes.
The surface gradient is defined, involving the surface covariant derivative of a scalar function.
The surface directional derivative is discussed, resulting from the dot product of the surface gradient and a unit vector in the tangent plane.
The surface Laplacian is defined, combining divergence operations and working similarly to its Euclidean counterpart.
The surface Boss-Vial formula is presented for evaluating divergence or Laplacian in surface coordinates.
The video concludes by demonstrating the application of tensor calculus to curved surfaces as a generalization of Euclidean space.
Examples of gradient, divergence, and Laplacian on cylindrical and toroidal surfaces are provided without detailed calculations.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: